Усовершенствованный метод Эйлера
Х
арактерной
особенностью метода является использование
в качестве направления поиска каждой
последующей точки численного решения
касательной, определяемой в центре
отрезка [xk,
xk+1].
Как видно на рис.4 для k
= 0, последовательно выполняются два
шага по методу Эйлера.
Первый из них используется для вычисления тангенса угла наклона касательной в средней точке отрезка [xk, xk+1]
,
,
,
Рис.4.
После этого делается второй шаг – для вычисления новой точки
,
.
Если тангенсы углов наклона касательных заменить на правую часть дифференциального уравнения f(x, y), то приведённые выше формулы для выполнения одного шага по усовершенствованному методу Эйлера сведутся к следующим
,
,
,
.
Этот метод является методом второго порядка точности. Он даёт меньшую погрешность численного решения на шаге h, чем метод Эйлера. Его абсолютная погрешность εабс(xk+1, h) на каждом шаге пропорциональна величине h3, а решение совпадает с истинным в случае, когда оно представимо квадратичной функцией y = a1+ a2x + a3x2. Однако это достигается тем, что его трудоёмкость увеличивается примерно в два раза, поскольку для одного шага приходится два раза вычислять значение правой части дифференциального уравнения.
Метод Рунге–Кутта (C.Runge 1895, W.Kutta 1901)
Под наименованием «метод Рунге–Кутта» принято подразумевать целое семейство методов численного решения задачи Коши, объединенных одной идеей выбора некоторого усреднённого направления поиска каждой новой точки приближённого решения. Алгоритм одного из этих методов: метода Рунге–Кутта 4-го порядка, строится по следующей схеме. Из начальной точки, как это можно видеть на рис.5 для k = 0, в направлении касательной делается шаг по методу Эйлера на величину h/2 и в полученной точке вычисляется тангенс угла наклона касательной
,
,
,
.
И
з
начальной точки по найденному направлению
делается второй шаг на ту же величину
и определяется тангенс угла наклона во
второй средней точке
,
.
Третий
шаг делается опять из начальной точки
по последнему найденному направлению
(
),
но на шагh,
где опять находится тангенс угла наклона
касательной
,
,
.
Последний шаг из начальной точки на величину h делается по присущему этому методу осреднённому направлению и находится ордината следующей точки приближённого решения
Рис.5.
.
Описанные действия, необходимые для получения координат каждой последующей точки приближённого решения, реализуются в виде следующей последовательности вычислений по формулам
,
,
,
,
,
.
Получающееся численное решение имеет на каждом шаге h погрешность εабс(xk+1, h), которая пропорциональна величине h5. Оно совпадает с истинным решением в случае, когда оно – многочлен четвёртого порядка y = a1+ a2x + a3x2+ a4x3+ a5x4.
Оценка погрешностей методов
Как уже отмечалось выше, при использовании метода Эйлера на каждом шаге положение следующей точки решения, вычисляется с использованием информации о правой части f(x, y) уравнения только в крайней левой точке отрезка [xk, xk+1]. В результате его абсолютная погрешность на каждом шаге пропорциональна величине h2
,
где
.
В
формуле для Ck+1
в качестве функции
используется некая промежуточная
функция, график которой располагается
между графиками приближённого и
неизвестного точного решений.
Аналогичные соотношения для оценки абсолютных погрешностей на каждом шаге можно привести для усовершенствованного метода Эйлера
,
где
и метода Рунге–Кутта 4-го порядка
,
где формула для Ck+1 не приводится из-за своей громоздкости.
Так как на отрезке интегрирования дифференциального уравнения требуется выполнить несколько шагов, то общая абсолютная погрешность вычисления приближённого решения в точке xn будет складываться из погрешностей каждого отдельного шага и погрешностей, которые они порождают на последующих шагах. Она имеет оценку
,
где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода Эйлера и m = 5 для метода Рунге–Кутта 4-го порядка, а параметры Cmax и q определяются следующим образом
,
.
Такое вычисление абсолютных погрешностей решения задачи Коши затруднено, так как требует решения дополнительной, зачастую даже более сложной, задачи поиска максимума высших производных правой части уравнения. Поэтому чаще для вычисления погрешности методов используют апостериорные оценки, базирующиеся на правиле Рунге (правило двойного счёта), идея которого описана в разделе «Вычисление определённых интегралов». Его основное соотношение, справедливое для всех способов приближённого решения задачи Коши, имеет вид
,
где y(xk, h) и y(xk, 2h) – приближённые значения решения, вычисленные в точке xk при шагах интегрирования, отличающихся друг от друга в два раза.
В качестве относительной погрешности решения задачи Коши на отрезке [x0, xn] его построения, часто используют её интервальную оценку, равную отношению абсолютной погрешности к максимальному значению модуля решения на данном отрезке
.
Работа методов и оценка погрешности получаемых результатов может быть проиллюстрирована на примере построения приближённого решения задачи Коши для уравнения
с начальным условием y(0) = 0 на отрезке [0, 0.4] с шагомh= 0.1.
Решение задачи методом Эйлера. В соответствии с алгоритмом метода расчётная схема может быть представлена в виде следующих соотношений
.
Поэтому, пошаговый процесс построения решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом
,
,
,
,
.
Для оценки погрешности полученного решения необходимо повторить проделанные расчёты с удвоенным шагом интегрирования h = 0.2
,
,
.
Полученные результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1
,
,
,
.
Решение задачи усовершенствованным методом Эйлера. В данном случае расчётная схема метода представляется в виде соотношений
В соответствии с этим процесс построения решения с шагом интегрирования h = 0.1 будет иметь вид
,
,
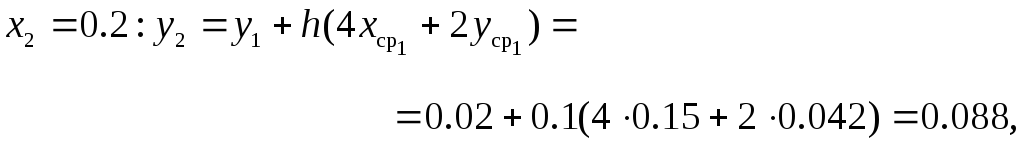
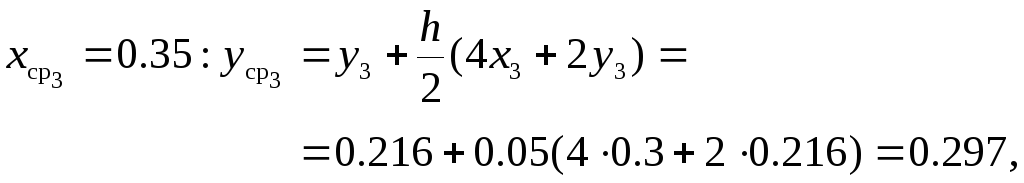
Аналогично предыдущему примеру, где реализован метод Эйлера, для вычисления погрешности решения с шагом h = 0.1 повторяются расчёты с шагом h = 0.2
,
,
Отсюда абсолютная и относительная погрешности решения с шагом h = 0.1 будут соответственно равны
,
,
,
,
.