
- •Численные методы
- •Содержание
- •Введение
- •1. Вычисление определенных интегралов Справочная информация
- •Формула средних прямоугольников
- •Формула трапеций
- •Формула Симпсона (j.Gregory(Грегори)1668,Th.Simpson1743)
- •Пример решения в среде Matlab
- •Контрольные задания
- •2. Решение нелинейных уравнений Справочная информация
- •Метод простых итераций Метод основывается на приведении исходного уравнения к форме
- •Относительная разница между значениями приближения корня на третьей и четвёртой итерациях составляет
- •Метод хорд
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •3. Решение систем линейных алгебраических уравнений Справочная информация
- •Метод Гаусса с выбором главного элемента
- •Метод простых итераций
- •О выборе метода решения систем уравнений
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •4. Интерполяция таблично заданных функций Справочная информация
- •Кусочно-линейная интерполяция
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •5. Аппроксимация таблично заданных функций Справочная информация
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •6. Решение задачи коши для обыкновенных дифференциальных уравнений 1-го порядка Справочная информация
- •Усовершенствованный метод Эйлера
- •Оценка погрешностей методов
- •Программное обеспечение
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •7. Решение задачи коши для нормальных систем обыкновенных дифференциальных уравнений и уравнений высших порядков Справочная информация
- •Метод Эйлера
- •Усовершенствованный метод Эйлера
- •Оценка погрешностей методов
- •Пример решения на пэвм в среде Matlab
- •Контрольные задания
- •Приложение. Основы работы в среде matlab Интерфейс среды
- •Переменные и константы
- •Арифметические операторы
- •Операторы отношения
- •Логические операторы
- •Элементарные функции
- •Простейшие способы ввода–вывода информации
- •Векторы и матрицы
- •Оператор двоеточие «:»
- •Оператор разветвления if
- •Операторы циклов
- •Вывод информации в файл
- •Форматный вывод информации
- •Ввод данных из файла
- •Построение графиков
- •Сообщения об ошибках и исправление ошибок
- •Список литературы
Пример решения на пэвм в среде Matlab
Пусть
надо интерполировать по пяти точкам
таблично заданную функцию с помощью
кусочно-линейной интерполяции, многчленом
Лагранжа и кубическими сплайнами.
Абсциссы узловых точек известны: х= 0.5; 1.5; 3.0; 4.0; 5.0, а их ординаты вычисляются
как значения функции![]() .
.
В случае кусочно-линейной интерполяции можно непосредственно воспользоваться соотношениями, приведёнными в этом разделе, и написать следующую программу
xk=[0.5,1.5;1.5,3;,3,4;4,5] задание концов отрезков интерполяции
yk=cos(2*xk)-xk*exp(-xk^2) вычисление значений функции на концах отрезков
for i=1:4
C(i)=(yk(i,2)-y(i,1))/(xk(i,2)-xk(i,1));
end
N=10; задание числа промежуточных точек на каждом отрезке
for i=1:4 цикл расчёта значений интерполяционной функции
dx=(xk(i,2)-xk(i,1))/N; вычисление шага по х
j=N*(i-1); вычисление сквозного номера точки
xk1(j+1:j+11)=xk(i,1):dx:xk(i,2) абсцисса i-й промежуточной точки
yk1(j+1:j+11)=yk(i,1)+C(i)*(xk1(j+1:j+11)-xk(i,1))
end
plot(xk1,yk1,'k --',x,y,'b s' ),grid построение графика
При её запуске на выполнение в командном окне высвечиваются следующие данные
xk =
0.5000 1.5000
1.5000 3.0000
3.0000 4.0000
4.0000 5.0000
yk =
0.1509 -1.1481
-1.1481 0.9598
0.9598 -0.1455
-0.1455 -0.8391
а в графическом окне выводится изображение, показанное на рис.7, где интерполирующая кусочно-линейная функция построена черным пунктиром, а исходные узловые точки – голубыми квадратами
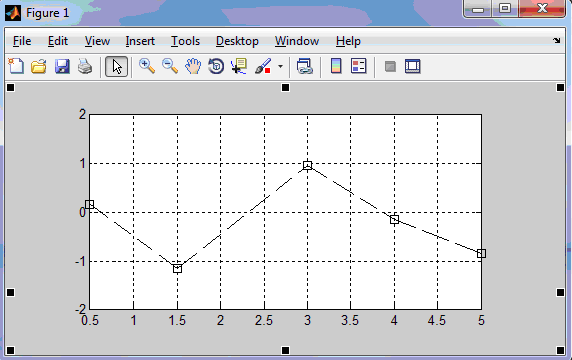
Рис.7.
Для реализации в среде Matlab’а интерполяции с помощью полинома Лагранжа надо сначала задать формулу для вычисления рассматриваемой функции и сохраним её вm-файле с именемfun:
function z = fun(x)
z=cos(2*x)-x.*exp(-x.^2);
Далее в новом m-файлeс именем, например,interpol.mследует обратиться к встроенной функцииpolyfit, которая с помощью соотношений для многочлена Лагранжа вычисляет значенияСкоэффициентов степенного многочлена
C=polyfit(X,Y,n).
Входными параметрами этой функции являются массивы XиY, содержащие координаты узловых точек, и степень полиномаn. Массив значений коэффициентов степенного многочлена имеет размерn+1.
Текст m-файла с программой для расчета многочлена и вывода графиков может иметь вид:
X=[0.5,1.5,3,4,5]
Y=fun(X);
C=polyfit(X,Y,4)
x1=0:0.1:5;
Y1=fun(x1);
Y2=C(5).*1+C(4).*x1+C(3).*x1.^2+C(2).*x1.^3+C(1).*x1.^4;
plot(X,Y,'b s',x1,Y2,'g-',x1,Y1,'r--')
Запуск m-файлаinterpol.mна выполнение позволяет получить в командном окне следующий результат:
C =
0.2093 -2.4794 9.6596 -13.6064 4.8361
а графическом окне (см. рис.8) изображение узловых точек (голубые квадраты), интерполируемой функции (красный пунктир) и интерполирующего степенного многогочлена (зелёная линия).
При необходимости интерполяции таблично заданной функции кубическим сплайном можно воспользоваться встроенной в среду Matlabфункциейcsape. Самый простой вариант обращения к ней выглядит следующим образом:
pp=csape(x,y)
где xиy– массивы со значениями абсцисс и ординат узловых точек. Функцияcsapeвозвращает структуруpp, содержащую информацию о построенном сплайне.
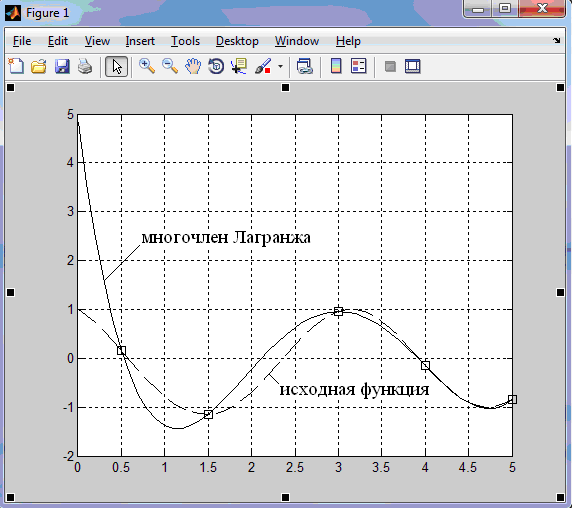
Рис.8.
По умолчанию, функция csapeнакладывает на сплайн следующие условия в граничных точках: значение производной сплайна в граничной точке совпадает со значением производной полинома третьей степени, проходящего через данную точку и ближайшие три.
Для иного задания условий в граничных точках есть несколько способов. Простейшие условия в граничных точках указываются при помощи дополнительного входного аргумента – строки:
вторая производная на концах отрезка построения сплайна равна нулю
pp=csape(x,y,'variational');
третьи производные сплайна на стыке двух крайних отрезков равны
pp=csape(x,y,'not-a-knot').
Третьим входным аргументом функции csapeможет быть не только текстовая строка, но и векторcondsиз двух элементов, содержащий значения 0, 1 или 2:
pp=csape(x,y,conds).
С помощью параметра condsреализуются более широкие возможности для постановки условий в граничных точках. Некоторые из них описаны ниже.
Если conds=[1 1], то на обоих концах отрезка интерполяции заданы значения первой производной сплайна. При этом возможны два вида обращения к функции csape:
pp=csape(x,[A y B],[1 1]) – в этом случае считается, что на концах отрезка интерполяции числами A и B заданы первые производные:
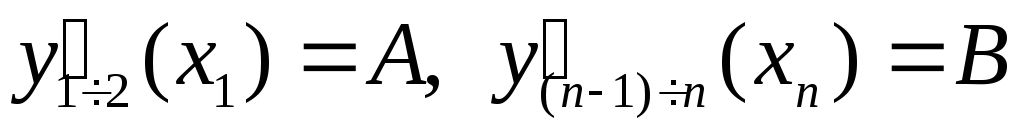 ;
;pp=csape(x,y,[1 1]) – в этом случае значение производной
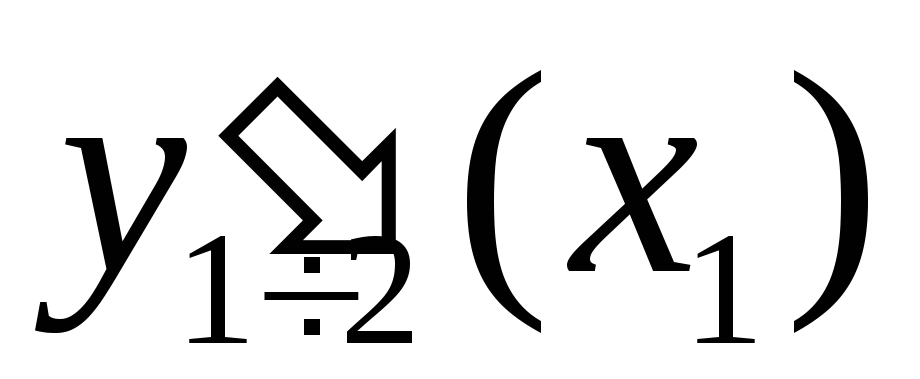 совпадает со значением первой производной
полинома третьего порядка, построенного
по узловым точкам с абсциссамиx1,
x2,
x3
и x4,
а значение производной
совпадает со значением первой производной
полинома третьего порядка, построенного
по узловым точкам с абсциссамиx1,
x2,
x3
и x4,
а значение производной
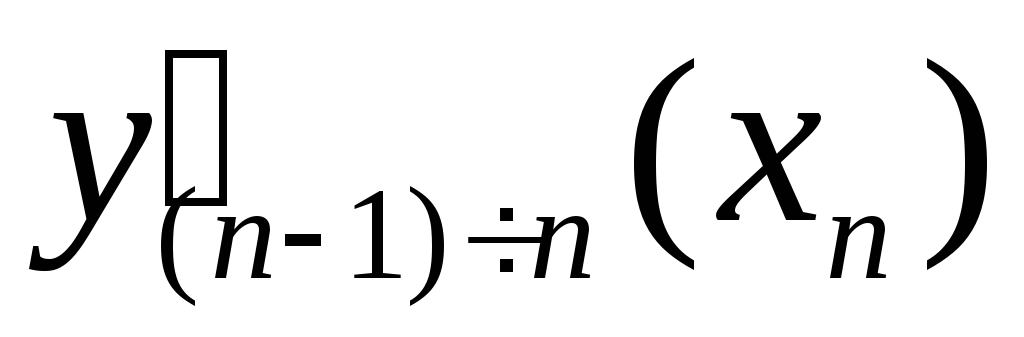 – со значением первой производной
полинома, построенного по узловым
точкам с абсциссамиxn–3,
xn–2,
xn–1
и xn.
– со значением первой производной
полинома, построенного по узловым
точкам с абсциссамиxn–3,
xn–2,
xn–1
и xn.
Если conds=[2 2], то на обоих концах отрезка интерполяции заданы значения второй производной сплайна. При этом возможны два вида обращения к функции csape:
pp=csape(x,[A y B],[2 2]) – в этом случае на концах отрезка интерполяции числами A и B заданы вторые производные:
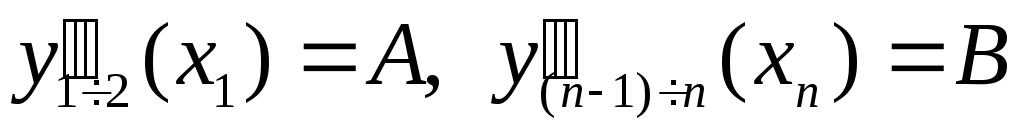 ;
;pp=csape(x,y,[2 2]) – в этом случае считается, что на концах отрезка интерполяции заданы нулевые вторые производные:
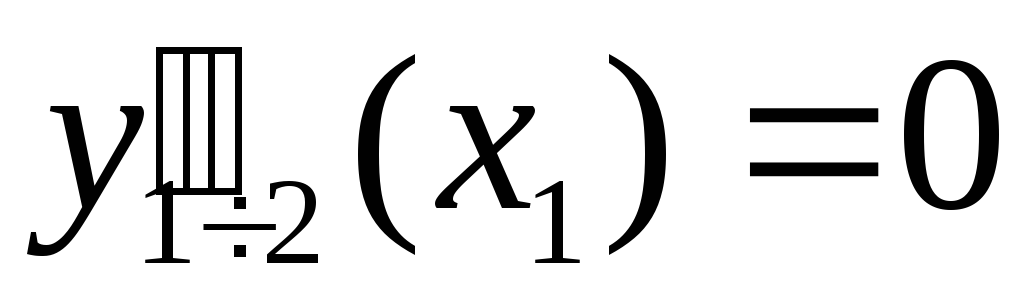 и
и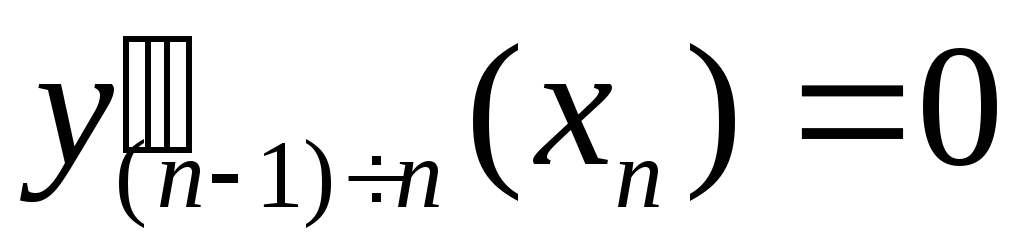 .
.
Если conds=[1 2], то на левой границе отрезка интерполяции задано значение первой производной сплайна, а на правой – второй производной. При этом возможны два вида обращения:
pp=csape(x,[A y B],[1 2]) – на левой границе задана первая производная
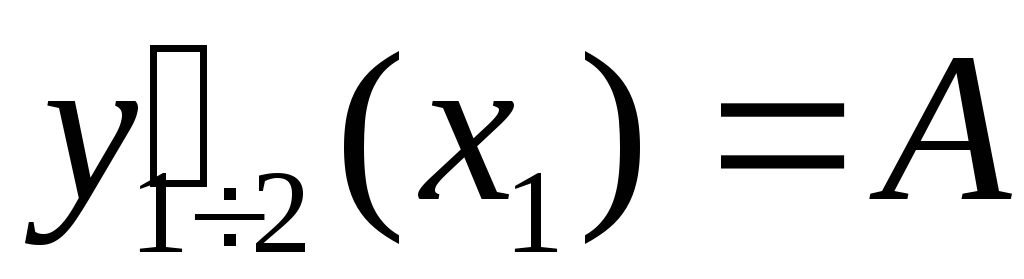 ,
а на правом – вторая производная
,
а на правом – вторая производная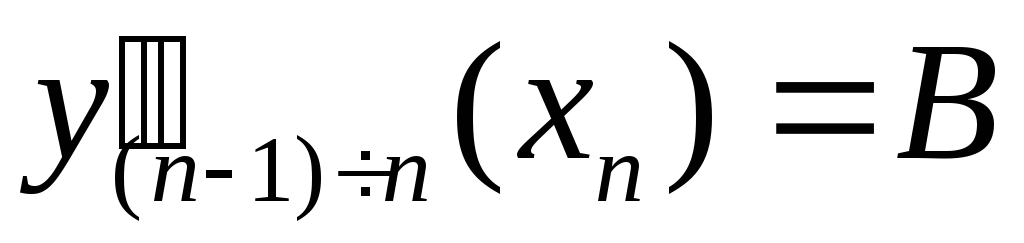 ;
;pp=csape(x,y,[1 2]) – в этом случае считается, что первая производная в левой точке отрезка интерполирования
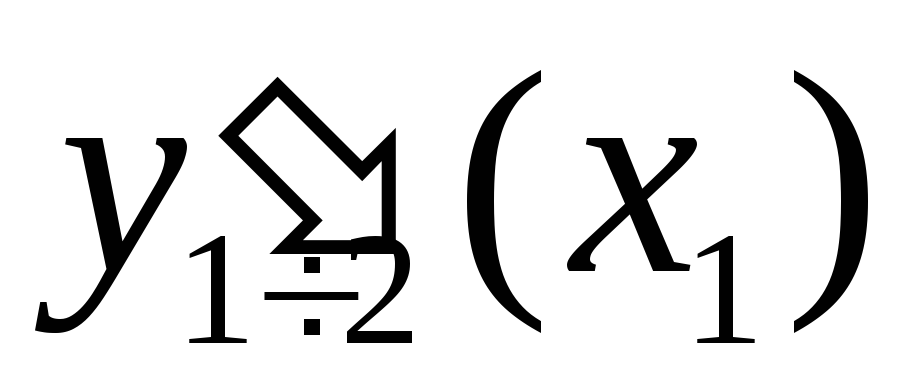 совпадает со значением первой производной
полинома третьей степени в этой точке,
построенного по абсциссам узловых
точекx1,
x2,
x3
и x4,
а в правой точке – задана нулевая вторая
производная
совпадает со значением первой производной
полинома третьей степени в этой точке,
построенного по абсциссам узловых
точекx1,
x2,
x3
и x4,
а в правой точке – задана нулевая вторая
производная
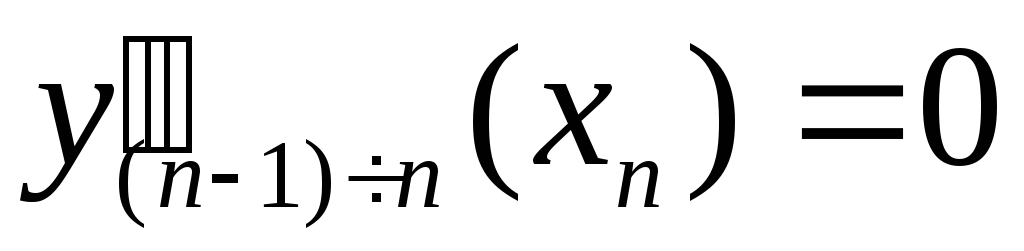 .
.
Если conds=[2 1], то аналогично предыдущему случаю, на левой границе отрезка интерполяции задано значение второй производной сплайна, на правой границе – первой производной.
Функция csapeвозвращает структуруpp, содержащую информацию о построенном сплайне. Эта структура имеет следующие поля:
form – форма сплайна. Его значение pp говорит о том, что сплайн строится в полиномиальной форме;
breaks – массив абсцисс узловых точек. В рассматриваемом примере заданы пять узловых точек с абсциссами 0.5, 1.5, 3.0, 4.0 и 5.0, и сплайн будет составлен из 4-х полиномиальных частей;
coefs – массив коэффициентов сплайна, каждая строка которого содержит коэффициенты его полиномиальных частей. В рассматриваемом примере это будет массив размером 4×4, так как на каждом из 4-х отрезков между узловыми точками используется кубический полином с 4-мя коэффициентами;
pieces – число полиномов, составляющих сплайн (в данном случае 4);
order – порядок сплайна (в данном случае 4, так как порядок равен степени кубического полинома плюс 1, иными словами он равен числу коэффициентов кубического полинома);
dim – размерность (в данном случае 1).
Для интерполяции заданной табличной функции сплайном можно воспользоваться простейшей формой записи функции csape. С этой программу интерполяции заданной функции многочленом Лагранжа следует дополнить следующими командами:
pp=csape(X,Y) вычисление параметров сплайна
D=pp.coefs вывод коэффициентов сплайна (массив 4*4)
hold on оператор для вывода графика в то же окно, что и ранее
for i = 1:4 цикл для вычисления значений сплайна на каждом из 4-х отрезков
X2 = X(i):0.01:X(i+1);
P=polyval(D(i,4),(X2-X(i)); вычисление значений сплайна на каждом отрезке
h=plot(X2,P,‘LineWidth’,2); построение графика сплошной линией толщины 2
end
Запуск её на выполнение даёт в командном окне следующий результат:
pp =
form: ‘pp’
breaks: [0.5000 1.5000 3 4 5]
coefs: [4x4 double]
pieces: 4
order: 4
dim: 1
D =
-0.4603 3.0320 -3.8706 0.1509
-0.8372 1.6510 0.8123 -1.1481
0.8964 -2.1162 0.1145 0.9598
0.1622 0.5730 -1.4287 -0.1455
При этом в графическом окне (см. рис.9) строятся четыре графика:
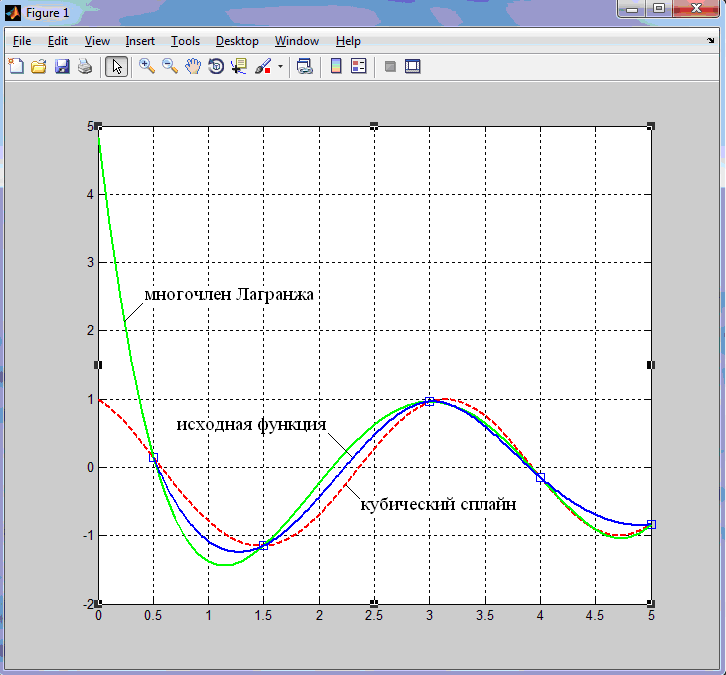
Рис.9.
исходная функция – красный пунктир, многочлен Лагранжа – зеленая сплошная линия и кубический сплайн – синяя сплошная линия.
