Главная

Лекция 2. Равновесие системы сил. Пара сил.

В данной лекции рассматриваются следующие вопросы

1. Проекция силы на ось и на плоскость.

2. Геометрический способ сложения сил.

3. Равновесие системы сходящихся сил.

4. Момент силы относительно центра или точки.

5. Теорема Вариньона о моменте равнодействующей.

6. Пара сил.

7. Момент пары.

8. Свойства пар.

9. Сложение пар.

10. Теорема о параллельном переносе силы.

11. Приведение плоской системы сил к данному центру.

12. Условия равновесия произвольной плоской системы сил.

13. Случай параллельных сил.

14. Решение задач.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

 

 

Проекция силы на ось и на плоскость.

Перейдем к рассмо­трению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проек­ции данной силы на любые параллельные и одинаково направлен­ные оси равны друг другу. Этим удобно пользоваться при вычисле­нии проекции силы на ось, не лежащую в одной плоскости с силой.

Рис. 12

 

Обозначать проекцию силы  на ось Ох будем символом . Тогда для сил, изображенных на рис. 12, получим:

,    .

Но из чертежа видно, что , .

Следовательно,

, ,

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным на­правлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпен­дикулярна к оси, то ее проекция на ось равна нулю.

Рис.13    

Проекцией силы  на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы  на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим чис­ленным значением, но и направлением в плоскости Оху. По модулю , где  — угол между направ­лением силы  и ее проекции .

В некоторых случаях для нахож­дения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось ле­жит, а затем найденную проекцию на плоскость спроектировать на данную ось.                  Например, в случае, изображенном на рис. 13, найдем таким способом, что

 

Геометрический способ сложения сил.

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил , , …,  (рис. 14, a), откладываем от произвольной точки О (рис. 14, б) век­тор Oa, изображающий в выбранном масштабе cилу F₁, от точки aоткладываем вектор , изображающий силу F₂, от точки b откла­дываем вектор bc, изображающий силу F₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F_n. Соединяя начало первого вектора с концом последнего, получаем вектор = , изображающий геометрическую сумму или главный вектор слагаемых сил:

   или  

От порядка, в котором будут откладываться векторы сил, модуль и направление  не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Рис.14

 

Фигура,  построенная на рис. 14,б, называется силовым (в общем случае векторным) многоугольником. Таким обра­зом, геометрическая сумма или главный вектор несколь­ких сил изображается замы­кающей стороной силового многоугольника, построенно­го из этих сил (правило сило­вого многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора  - в сторону противоположную.

Равнодействующая сходящихся сил. При изучении статики мы будем последовательно переходить от рассмотрения более простых систем сил к более сложным. Начнем с рассмотрения си­стемы сходящихся сил. Сходящимися  называются  силы,  линии  дей­ствия которых пересекаются в одной точке (см. рис. 14, а). 

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 14, а в точке А).

Последовательно применяя аксиому параллелограмма сил, прихо­дим к выводу, что система сходящихся сил имеет равнодей­ствующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы , , …,  сходятся в точке A(рис. 14, а), то сила, равная главному вектору , найденному построением силового мно­гоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

 

Равновесие системы сходящихся сил.

Из законов меха­ники следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инер­ции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравно­вешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравнове­шенных сил.

Для равновесия приложенной к твердому телу системы сходя­щихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовле­творять сами силы, можно выразить в геометрической или аналити­ческой форме.

1. Геометрическое условие равновесия. Так как равнодействующая  сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то  может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда много­угольник замкнется.

Следовательно, для равновесия системы, сходящихся сил необ­ходимо и достаточно, чтобы силовой многоугольник, построен­ный из этих сил, был замкнут.

2. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой

.

Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно , , , т. е. когда действующие на тело силы будут удовлетворять равенствам:

    

Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия

  

Равенства выражают также необходимые условия (или уравнения) равновесия свободного твердого тела, находящегося под действием сходящихся сил.

Пример 1. На рис.15 показаны три силы. Проекции сил  и  на оси х, у, z очевидны:

          

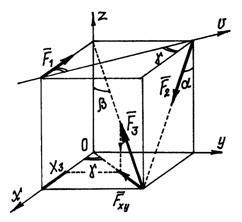
Рис.15

 

Рис. 2.4.

А чтобы найти проекцию силы  на ось х нужно использовать пра­вило двойного проектирования.

Проектируем силу сначала на плос­кость хОу, в которой расположена ось (рис.15), получим вектор , величиной  а затем его проектируем на ось х: 

Аналогично действуя, найдём проекцию на ось у: .

Проекция на ось z находится проще: .

Нетрудно убе­диться, что проекции сил на ось V равны:

  

При определении этих проекций удобно воспользоваться рис.16, видом сверху на распо­ложение сил и осей.

Рис.16

 

Вернёмся к системе сходящихся сил (рис. 17). Проведём оси координат с началом в точке пересечения линий действия сил, в точке О.

Мы уже знаем, что равнодействующая сил . Спроектируем это векторное равенство на оси. Получим проек­ции равнодействующей  на оси x, y, z:

                                                                                                      

Они равны алгебраическим сум­мам проекций сил на соответствующие оси. А зная проекции равнодействую­щей, можно определить и величину её как диагональ прямоугольного парал­лелепипеда  или

.                                       

Направление вектора  найдём с помощью направляющих косинусов (рис.17):

  

Рис.17

 

Пример 2. На шар, вес которого Р, лежащий на горизонтальной плоско­сти и привязанный к ней нитью АВ, действует сила F (рис.18). Определим реакции связей.

Рис.18

 

Следует сразу заметить, что все задачи статики решаются по одной схеме, в определённом порядке.

Продемонстрируем ее на примере решения этой задачи.

1. Надо выбрать (назначить) объект равновесия – тело, равновесие ко­торого следует рассмот­реть, чтобы найти неиз­вестные.

В этой задаче, ко­нечно, объект равновесия – шар.

2. Построение рас­чёт­ной схемы. Расчётная схема – это объект рав­новесия, изображённый отдельно, свободным телом, без свя­зей, со всеми силами, действую­щими на него: реакциями и остальными силами.

Показываем реакцию нити  и нормаль­ную реакцию плоскости –  (рис.18). Кроме них на шар действуют заданные силы  и .

3. Надо установить какая получилась система сил и составить со­ответствующие уравнения равновесия.

Здесь получилась система сходящихся сил, расположенных в плос­кости, для которой составляем два уравнения (оси можно проводить произвольно):

 ,

 

4. Решаем систему уравнений и находим неизвестные.

 

По условию задачи требовалось найти давление шара на плоскость. А мы нашли реакцию плоскости на шар. Но, по определению следует, что эти силы равны по величине, только давление на плоскость будет направлено в противоположную сторону, вниз.

Пример 3. Тело весом Р прикреплено к вертикальной плоскости тремя стержнями (рис.19). Определим усилия в стержнях.

Рис.19

 

В этой задаче объект равновесия – узел С вместе с гру­зом. Он нарисован отдельно с реак­циями, усилиями в стержнях , , , и весом . Силы образуют пространственную систему сходящихся сил. Составляем три уравнения равно­весия:

 

 

 

Из первого уравнения следует: S₂ = S₃. Тогда из третьего:

 а из второго: 

Когда мы направляли усилие в стержне от узла, от объекта равнове­сия, предполагали, что стержни работают на растяжение. Усилие в стержне CDполучилось отрицательным. Это значит – стержень сжат. Так что знак усилия в стержне указывает как работает стержень: на растяжение или на сжатие.

 

Момент силы относительно центра (или точки).

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее момен­том

Рассмотрим силу , приложенную в точке А твердого тела (рис. 20). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы , на­зывается плечом силы  от­носительно центра О. Так как точку приложения силы можно произвольно переме­щать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть: 1) от модуля силы F и длины плеча h; 2) от поло­жения плоскости поворота ОАВ, проходящей через центр О и силу F; 3) от направления поворота к этой плоскости.

Рис.20

 

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы  относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы  относительно центра О будем обозначать сим­волом m₀(F). Следовательно,

В дальнейшем условимся считать, что момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода ча­совой стрелки, и знак минус, - если по ходу часовой стрелки. Так, для силы , изображенной на рис.20,а, момент относительно центра О имеет знак плюс, а для силы, показанной на рис.20,б, - знак ми­нус.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О(плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью тре­угольника ОАВ (рис. 20,б)

Этот результат следует из того, что

 

Теорема Вариньона о моменте равнодействующей.

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил от­носительно любого центра равен алгеб­раической сумме моментов слагаемых сил относительно того же центра.

Рис.21

 

Рассмотрим систему сил , , …, , сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие  выражения  моментов m₀(), m₀(), … . По формуле . Но, как видно из рисунка, , где F_1x - проекция силы  на ось Ох; сле­довательно  

.                                                                   

Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил , , …, , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

или,

.

 

Пара сил. Момент пары.

Парой сил (или просто парой) называются две силы, равные по ве­личине, параллельные и направленные в противоположные стороны (рис.22). Очевидно, ,  и .

Рис.22

 

Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:

.

Расстояние a между линиями действия сил называется плечом пары.

Если пара вращает тело против часовой стрелки, момент её считается положительным (как на рис.22), если по часовой стрелке – отрицательным.

Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.

Вектор момента пары  направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть от­туда, увидим вращение тела против часовой стрелки (рис. 23).

Нетрудно доказать, что вектор мо­мента пары  – есть вектор этого векторного произведения (рис. 23). И за­метим, что он равен вектору момента силы  относительно точки А, точки приложения второй силы:

.

О точке приложения вектора  бу­дет сказано ниже. Пока приложим его к точке А.

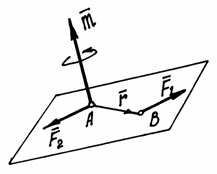
Рис.23

 

Свойства пар

1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.

2) Найдём сумму моментов сил  и  составляющих пару, относительно какой-либо точки О (рис.24).

Рис.24

 

Покажем радиусы-векторы точек А₁ и А₂ и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О

.

Но . Поэтому .

Но , а .

Значит .

Момент пары сил относительно любой точки равен моменту этой пары.

Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, рав­ный моменту этой пары .

Поэтому можно сформулировать ещё два свойства.

3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.

4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F₁=F₂=5 H и плече а = 4 см момент пары m = 20 Hсм. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Нсм и действие пары на тело не из­менится.

Все эти свойства можно объединить и, как следствие, сделать вы­вод, что пары с одинаковым вектором момента  и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.

Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m. Или, если это пространственная конструкция, по­казывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары  – свободный вектор.

И ещё одно дополнительное замечание. Так как момент пары ра­вен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары  на эту ось:

,

где  – угол между вектором  и осью z.

 

Сложение пар

Пусть даны две пары с моментами m₁ и m₂, расположенные в пере­секающихся плоскостях (рис.25).

Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а об­разующих вторую пару: .

Эти пары показаны на рис.25, где , . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересе­чения плоскостей.

Рис.25

 

Рис. 4.4.

Сложив силы, приложенные к точкам А и В, построением паралле­лограммов, получим их равнодействующие  и . Так как , то эти силы  и  будут образовывать пару, мо­мент которой , где  – радиус-вектор точки В, совпадающий с АВ.

Так как , то момент полученной пары

.

Следовательно, в результате сложения пар, расположенных в пере­секающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоско­стях, получим пару с моментом

.                                                                         

Конечно, эта результирующая пара будет располагаться в плоско­сти перпендикулярной вектору .

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие рав­новесия пар

.                          

Если пары расположены в одной плоско­сти, векторы моментов их будут параллельны. И момент результирующей пары можно опре­делить как алгебраическую сумму моментов пар.

Рис.26

 

Например, пары, показанные на рис.26, расположены в одной плоскости и моменты их:

m₁=2 Hсм , m₂=5 Hсм, m₃=3 Hсм. Пары урав­нове­шива­ются, потому что алгебраиче­ская сумма их моментов равна нулю:

.

 

Теорема о параллельном переносе силы.

Равнодействующая системы сходящихся сил непосредственно находится с помощью аксиомы параллелограмма сил. Для двух параллельных сил эта задача была решена путем приведения их к сходящимся силам. Очевидно, что анало­гичную задачу легко будет решить и для произвольной системы сил, если найти и для них метод приведения к силам, приложенным в одной точке.

Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.

Попробуем силу  (рис. 27) перенести в какую-нибудь точку О, не расположенную на линии дей­ствия.

Рис.27

 

Приложим к этой точке две урав­новешивающиеся силы  и , парал­лельные силе  и равные ей по вели­чине: 

В результате получим силу , приложенную к точке О. То есть мы как бы перенесли заданную силу  из точки А в точку О, но при этом появилась пара, образованная си­лами  и . Момент этой пары , равен моменту заданной силы  относительно точки О.

Этот процесс замены силы  равной ей силой  и парой называ­ется приведением силы к точке О.

Точка О называется точкой приведения; сила , приложенная к точке приведения, – приведённой силой. Появившаяся пара – присоеди­нённой парой.

 

Приведение плоской системы сил к данному центру.

          Пусть на твердое тело действует какая-нибудь система сил , , …, , лежащих в одной плоскости. Возьмем в этой плоскости произвольную точку О, которую назовем центром приведения, и, перенесем все силы в центр О (рис. 28, а). В результате на тело будет действовать система сил  приложенных в центре О, и система пар, моменты которых будут равны: 

 

Рис.28

 

Силы, приложенные в центре О, можно заменить одной силой , приложенной в том же центре; при этом  или  

Точно так же, по теореме о сложении пар, все пары можно заменить одной парой, лежащей в той же плоскости. Момент этой пары  или 

Величина , равная геометрической сумме всех сил системы, называется, как известно, главным вектором системы; величину М_о, равную сумме моментов всех сил системы относительно центра О, будем называть главным моментом системы относительно цент­ра О. В результате мы доказали следующую теорему: всякая пло­ская система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М₀, равным главному моменту системы относительно центра О (рис. 28, в).

 

Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.

Здесь О - любая точка плоскости.

Найдем вытекающие из равенств аналитические условия равновесия.

Величины R и М_о определяются равенствами:

  

где   Но R может равняться нулю только тогда, когда одновременно R_x = 0 и R_y = 0. Следовательно, условия будут выполнены, если будет:

    

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных  в плоскости действия сил и не лежащих на одной прямой,  были равны нулю.

;   ;  

 

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оупараллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х  равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:   

Где ось Оу параллельна силам.

Рис.29

 

Статически определимые и статически неопределимые задачи.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных.

Задачи, в которых число неизвестных не больше числа независимых условий равновесия  для данной системы сил, приложенных к твердому телу, называются статически определимыми.

В противном случае задачи статически неопределимы.

 

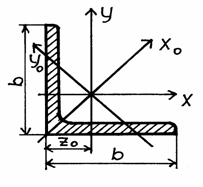
Лекция 4 (продолжение). Примеры решения задач по геометрическим характеристикам плоских сечений и задачи для самостоятельного решения

 

Геометрические характеристики сложных сечений

Пример 1.

Сечение стержня представляет собой несимметричную фигуру, показанную на рис. 1. Требуется найти положение главных центральных осей инерции фигуры и моменты инерции относительно этих осей.

                                 Рис.1

 

Решение.

Найдем положение центра тяжести фигуры по формулам ;  . Разобьем фигуру на три простые: треугольник I, прямоугольник II и квадрант круга Ш. Площадь всей фигуры

Для определения статических моментов выберем вспомогательные оси , проходящие через центр тяжести прямоугольника II (рис. 2). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат . Суммарные статические моменты

 

Координаты центра тяжести

отложены на рис. 2.

                                                                          Рис.2

 

Проведем через центр тяжести центральные оси  (см. рис. 2) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и Ш используем формулы ,  ,  . Моменты инерции относительно собственных осей  прямоугольника, треугольника и квадранта круга вычисляем соответственно по формулам

;           ;           ,

;           ;          .             

;       .               

Отсюда

 

Теперь найдем положение главных осей инерции. Угол, на который надо повернуть ось , чтобы она стала главной осью, определяем по формуле :

;

;                .

В соответствии с правилом знаков откладываем отрицательный угол  по часовой стрелке и проводим главные центральные оси инерции Y, Z (см. рис. 2). Вычислим моменты инерции относительно этих осей по формуле :

;      .

Для проверки вычислений удобно использовать следующее свойство: сумма моментов инерций относительно двух любых пар ортогональных осей есть величина постоянная. Тогда должно быть

.

 В нашем примере .

Чтобы выяснить, какой момент инерции – максимальный или минимальный соответствует оси , исследуем знак второй производной функции  по формуле .

.

Положительный знак второй производной означает, что оси  соответствует минимальное значение момента инерции, т. е.

               

Найдем радиусы инерции относительно главных центральных осей по формуле  и построим эллипс инерции.

                            

Эллипс инерции показан на рис. 2. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура.

 

Пример 2.

Определить координаты центра тяжести и осевые моменты инерции сечения в виде круга радиусом r =3а с круговым отверстием  радиуса  r₀  = a, касающимся центра круга (см. рис.).

 

Решение.

Принимаем за 1-й элемент сплошной круг радиусом  r =3а, за второй элемент отверстие радиуса r₀  = a. Начальные оси проводим через центр тяжести 1-го элемента.

Тогда имеем:

;    ;

;  ;  .

Так как ось  р  является осью симметрии сечения, так же как и осями симметрии элементов сечения, то эта ось является центральной осью  у  и  . Следовательно, для определения положения центра тяжести сечения требуется определить только координату р_с

.

Координаты центров тяжести элементов относительно центральных осей:

;     ;     ;    . 

Осевые моменты инерции круга относительно собственных центральных осей определяются по формуле

.

Следовательно, имеем:

;     .

Определяем осевые моменты инерции сечения

;

.

Так как сечение имеет ось симметрии, то центробежный момент инерции сечения равен нулю и оси  у,  z  являются главными.

 

Пример 3.

Для фигуры, показанной на рис.1 определить положение главных осей инерции и главные моменты инерции.

Решение.

Выписываем основные исходные данные для каждой фигуры

Швеллер

S₁ = 10,9 см² ; I_x = 20,4 см⁴; I_y = 174 см⁴;  y₀ = 1,44 см;  h = 10 см

Неравнополочный уголок

S₃ = 6,36 см²; I_x = 41,6 см⁴; I_y = 12,7 см⁴; I_min = 7,58 см⁴;  = 0,387;  x₀ = 1,13 см;  y₀ = 2,6 см

Прямоугольник

S₂ = 40 см²

 см⁴.

 см⁴.

Вычерчиваем сечение в масштабе

Проводим произвольные оси координат

Определяем координаты центра тяжести сечения

см;

см.

Проводим центральные оси

см, см,

см,

см, см,

см.

Определяем осевые моменты инерции относительно центральных осей

Определяем центробежный момент инерции относительно центральных осей

Центробежный момент инерции для угловой прокатной стали относительно ее центра тяжести определяется по одной из следующих формул:

см⁴.

Знак центробежного момента инерции для угловой прокатной стали определяется согласно рис. 2, поэтому I_xy3 = -13,17 см⁴.

Определяем положение главных осей инерции

               Рис.2

 

Определяем главные моменты инерции

 

Пример 4.

Определить координаты центра тяжести сечения (рис.1), составленного из прокатных профилей.

                  

                             Рис.1

 

Решение:

Из таблиц сортамента имеем:

для швеллера № 22а:  Z_o = 2,46 см;   А₁ = 28,8 см²;

для уголка 100х100х10:  Z_o = 2,83 см;  А₂ = 19,2 см².

Совмещаем вспомогательные оси u и v с центральными осями швеллера и выполняем вспомогательные вычисления в табличной форме

                     Рис.2

 

Номер вычисления	Координаты, см		Площадь Ai, cм2	Статические моменты, см3
	ui	vi		uiAi	viAi
1 2	0 5,29	0 8,17	28,8 19,2	0 101,6	0 156,9

 

Координаты центра тяжести

 см,

 см.

 

Пример 5.

Определить положение главных центральных осей и величины главных центральных моментов инерции данного сечения (см. рис.1).

                Рис.1

 

                       Рис. 2

 

Решение.

1. Определение моментов инерции относительно центральных осей хСy.  

По  таблице сортамента имеем:

швеллер № 22:  = 2330 cм⁴,   = 187 cм⁴,    А₁ = 28,8 см²;

уголок 100х100х10:  = 179 cм⁴,  А₂ = 19,2 см²;

центробежный момент инерции уголка относительно = 105 cм⁴.

Учитывая, что центральные оси xy проведены параллельно собственным осям элементов фигуры, для вычисления осевых и центробежного моментов инерции всего сечения воспользуемся формулами, представляя все необходимые вычисления в табличной форме:

Номер элемента	Координаты центра тяжести, см		Площадь Аi, см4	Моменты инерции площадей, см4
	xi	yi				Ixi			Iyi		xiyiAi	Ixiyi
1	-2, 12	-3, 27	28,8	2330	308	2638	187	129	316	0	200	200
2	3, 17	4, 90	19,2	179	461	640	179	193	372	105	298	403
			48	2509	769	3278	366	322	688	105	498	603

2. Определение главных центральных моментов инерции сечения. По формуле имеем

,

Отсюда     I_max = I₁ = 3412 см⁴,      I_min = I₂ = 555 см⁴.

Ориентация максимальной главной оси определяется по формуле

= (3278-3412)/603 = -0,222,

откуда = -1230'.

3. Построение эллипса инерции. Главные радиусы инерции равны

 см;

  см.

Отложив радиусы инерции перпендикулярно к соответствующим осям в том же масштабе, в каком вычерчена фигура, строим на них, как на полуосях, эллипс инерции.

 

Пример 6.  

Для сложных составных поперечных сечений, не содержащих осей симметрии, предлагается следующий порядок расчета.

1) Сначала вычерчивается поперечное сечение. Случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте (рис.1). Каждому прокатному профилю присваивается порядковый номер. Наносим местные оси координат х_i, у_i, проходящие через известные центры тяжести i–го профиля. Оси х_i, у_iпараллельны случайным осям х, у соответственно.

2) Наносим на рисунок известные размеры сечения, взятые из задания или из соответствующих таблиц сортамента прокатной стали.

3) Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i–го профиля относительно случайных осей х, у; А_i – площадь сечения i–го профиля, – площадь поперечного сечения всего составного сечения; – осевые и центробежные моменты инерции i–го профиля относительно местных осей х_i, у_i.

4) Следуя предложенной методике, выпишем геометрические характеристики для поперечного сечения, изображенного на рис. 1:

х₁ = 25 см;  х₂ = 43,42 см;  х₃ = 36,11 см;  х₄ = 5,32 см;

у₁ = 24,8 см;  у₂ = 12 см;  у₃ = 4,89 см; у₄ = 21,64 см;   

   

5) С помощью формул

 

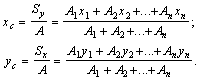
находим координаты центра тяжести всего поперечного сечения:

6) Наносим оси х_с, у_с, которые проходят через центр тяжести С всего составного поперечного сечения и определяем расстояния между осями х_с и х_i, а также между осями у_с и у_i:

а₁ = у₁ – у_с = 24,8 – 17,5 = 7,3 см;       b₁ = х₁ – х_с = 25 – 27,4 = –2,4 см;

а₂ = у₂ – у_с = 12 – 17,5 = –5,5 см;        b₂ = х₂ – х_с = 43,42 – 27,4 = 16,02 см;

а₃ = у₃ – у_с = 4,89 – 17,5 = –12,61 см; b₃ = х₃ – х_с = 36,11 – 27,4 = 8,71 см;

а₄ = у₄ – у_с = 21,64 – 17,5 = 4,14 см;   b₄ = х₄ – х_с = 5,32 – 27,4 = –22,08 см.

7) Используя формулы получаем выражения для вычисления осевых моментов инерции относительно центральных осей х_с и у_с всего поперечного сечения:

или окончательно:

            

 По формуле  находим значение центробежного момента инерции относительно осей х_с, у_с:

где, согласно рис. 1, имеем  так как швеллер и полоса имеют оси симметрии х₂ и х₁, у₁ соответственно.

Для вычисления для равнополочного уголка предварительно выпишем из таблицы сортамента «Уголки стальные горячекатаные равнополочные» = 2093 см⁴,= 540 см⁴,, (рис. 2, а).

Тогда формула  принимает вид:

Для вычисления для неравнополочного уголка (рис. 2, б) предварительно выпишем из таблицы сортамента

= 238,75 см⁴, = 784,22 см⁴, I_uv = 0, I_u = 142 см⁴,  = 0,388

и затем, согласно формуле  получаем:

Таким образом, формула для рассматриваемого случая принимает вид:

где = 0,388; = –21^о12^/  (рис.2, б), тогда

      

 Значение центробежного момента можно вычислить, используя формулу . Для этого рассмотрим рис. 2, в. Разобьем уголок на два прямоугольника с

 и .

В этом случае по формуле  получаем

Как видно, результаты очень близки по значениям.

Теперь можно приступить к определению центробежного момента всего составного сечения относительно осей хс, ус:

8) Главные оси инерции можно построить, повернув центральные оси х_с, у_с на угол  (рис. 1):

9) Величины главных моментов инерции определяем по формуле

Окончательно получаем, что I_max = 48582 см⁴, I_min = 13438 см⁴.

Полученные значения удовлетворяют условию :

Таким образом, определены все геометрические характеристики сложного составного поперечного сечения, показанного на рис.1.

 

Пример 7.

Определить положение главных центральных осей и вычислить главные центральные моменты инерции для сечения (см. рис.), состоящего из неравнобокого уголка №14/9 (ГОСТ 8510-57) и швеллера №24 (ГОСТ 8240-56).

Решение.

Разбиваем фигуру на части, геометрические характеристики которых можно взять из таблиц сортамента, на швеллер и уголок; через их центр тяжести c₁ и c₂ проводим центральные оси z₁, y₁ и z₂, y₂, параллельные их сторонам. Поскольку z₁ - ось симметрии швеллера, то она и ось y₁ являются его главными центральными осями. Главная центральная ось уголка v-v образует с его центральной осью z₂ угол .

Из таблиц сортамента имеем:

Для швеллера №24   F₁=30,6 см²

координаты центра тяжести

  

h=24 см     b=9 см

Для уголка №14/9   F₂=22,2 см²

    

координаты центра тяжести

  

1) Определим координаты центра тяжести всего сечения, для этого принимаем за исходные оси главные центральные оси швеллера z₁ и y₁ и согласно (4.4) получаем:

  

  

Через центр тяжести C проводим центральные оси z_c и y_c, параллельные проведенным ранее центральным осям швеллера и уголка.

Для проверки правильности определения координат центра тяжести, вычислим статические моменты относительно центральных осей z_c и y_c, которые должны быть равны нулю.

Получаем:

2) Вычислим осевые и центробежный моменты инерции всего сечения в системе центральных осей z_c, y_c по формулам:

для швеллера , т.к. оси z₁ и y₂ являются для швеллера главными центральными; для уголка  согласно сортамента.

3) Определяем угол  наклона главных центральных осей u и v относительно центральных осей z_c, y_c:

 

Поскольку угол  отрицательный, он откладывается по ходу часовой стрелки, а т.к. , то поворотом оси z на угол, меньший 45, мы получим направление главной центральной оси u, относительно которой главный момент инерции максимален I_u=I_max.

4) Главные моменты инерции определяем по формулам

  

Проверки: а) Определяем центробежный момент инерции относительно главных центральных осей , который должен быть равен нулю:

б) Определим главные центральные моменты инерции I_u и I_v по формулам:

I_u=I_max=3445,0 + 2585,6 = 6030,6 см⁴

I_v=I_min=3445,0 - 2585,6 = 859,4 см⁴

Максимальное расхождение составляет:

.

в) Должно удовлетворяться условие:

Расхождение составляет:

.

5. Определение моментов сопротивления сечения.

Наиболее удаленными точками от осей u и v являются точки A и B:

        

y_B = y_A = -17,94 см

По формулам получаем:

6. Радиусы инерции вычисляются по формулам (4.35), (4.36):

F = F₁ + F₂ = 30,6 +22,2 = 52,8 см²

Откладывая отрезки i_u=10,69 см и i_v=4,03 см перпендикулярно соответствующим осям, строим на них, как на полуосях, эллипс инерции (см. рис.).

 

Пример 8.

Для поперечного сечения (см. рис.1), состоящего из двутавра №10 и равнобокого уголка 50х50х5 мм, требуется:

1) определить положение центра тяжести сечения;

2) найти центральные осевые и центробежный моменты инерции сечения;

3) определить направление главных центральных осей инерции сечения (U и V);

4) вычислить главные центральные моменты инерции сечения.

                                                                                      Рис.1

Решение.

1. Выписываем из таблиц сортамента прокатных профилей  необходимые для расчета данные:

- Двутавр №10 (ГОСТ 8239-56);

 A₁ =12 см²;  b=5,5 см; h=10 см;  I_x= 198 см⁴;  I_y1= 17,9 см⁴.

- Уголок равнобокий 50х50х5 (ГОСТ 8509-57);

A= 4,8 см²; b = 5 см; z₀= 1,42 см; I_x= 11,2 см⁴ ; I_x0= 17,8 см⁴ ; I_y0= 4,63 см⁴

2. Вычерчиваем в масштабе сечение. Для определения положения центра тяжести составного сечения обозначим двутавр – I и равнобокий уголок – II и проведем собственные центральные оси X₁, Y₁ и X₂, Y₂. Проводим вспомогательные оси X, Y. Тогда координаты центра тяжести сечений I и II относительно осей X, Y:

 см;

 см;

см; 

см.

Координаты центра тяжести всего сечения:

 

где А₁ =12 см²; А₂ =4,8 см² – площади поперечных сечений.

Наносим эти размеры на чертеж и через полученный центр тяжести С проводим центральные оси X_c и Y_c. Проверяем правильность вычислений: центр тяжести составного сечения должен лежать на линии, соединяющей центры тяжести первого и второго сечений.

3. Вычисляем центральные осевые и центробежный моменты инерции составного сечения. Воспользуемся формулами для определения моментов инерции при параллельном переносе осей:

;  ;

;  ;                                                           (1)

;     .

где  m₁, m₂ – расстояние между параллельными осями X₁ и Х_С, X₂ и Х_С соответственно;

n₁, n₂ – расстояние между параллельными осями Y₁ и Y_c, Y₂ и Y_c соответственно.

На основании данных чертежа получим:

= 2,75 – 2,37 = 0,38 см;

 = –(2,27 – 1,42) = –0,95 см;

 = –(6,83 – 5) = –1,83 см;

 = 11,42 – 6,83 = 4,59 см.

Вычисляем центральные осевые моменты инерции всего сечения, равные сумме моментов инерции фигур, составляющих это сечение, с учетом формулы (1):

 = (17,9 +0,38²12) +(11,2 + (– 0,95)²4,8) = 19,63 + 15,53 = 352 см⁴;                                 (2)

 

 

= (198 + (– 1,83)²12) +(11,2  + 4,59²4,8) = 238,2 + 111,9 = 350,1 см⁴.                                   (3)

Центробежный момент инерции составного сечения вычисляем с учетом формул (1) аналогично:

  =

= (0 + 0,38(–1,83)12) + (– 6,58 + (– 0,95)4,594,8) = (– 8,34) + (– 27,5) =  – 35,8 см⁴.                          (4)                                     

В этой формуле для двутавра, являющегося симметричным сечением относительно собственных центральных осей, центробежный момент инерции  = 0, т.к. эти оси  главные центральные оси двутавра. Для равнобокого уголка (= 45º):

 ;      

                                Рис.2

 

Знак I_xy при различных положениях равнобоких и неравнобоких уголков выбирается согласно рисунок 2. В нашем случае берется знак минус.

4. Определим  направление главных центральных осей на основании вычислений по формулам (2), (3) и (4):

= –12º48’;  = –6º24’.

Угол  < 0, поэтому угол  = –6º24’ отложим от оси Х_С  в направлении часовой стрелки и проведем главную ось U, а ей перпендикулярно – главную ось V (рис. 2).

5. Вычислим значения главных центральных моментов инерции

 

I_max = 354 см⁴ = 354·10^-8 м⁴;

I_min = 31,2 см⁴ = 31,2·10^-8 м⁴.

Положение оси U(I_min) легко определить, т.к. эта ось, во-первых, пересекает сечение по наибольшему протяжению и, во-вторых, располагается ближе к той центральной оси инерции (оси Х_С), относительно которой центральный момент инерции имеет меньшую величину, т.е. (I_xc<I_yc).

Таким образом  I_V = I_min = 31,2·10^-8 м⁴,

I_U = I_max = 354 см⁴ = 354·10^-8 м⁴.

Проверка: ;

 см⁴;

 см⁴.

Т.к. оси V и U главные, то должно выполняться условие равенства нулю центробежного момента инерции, вычисленного относительно главных осей V и U, т.е.  = 0. Тогда при  = –6º25’ получим:

где     ,

.

 

Пример 9.

Задано составное сечение, состоящее из двутавра № 20, неравнобокого уголка 100х63х6 мм и пластины 240х20 мм. На рис. 1 представлено это сечение.

            Рис.1

 

Требуется:

1. Определить центр тяжести сечения.

2. Вычислить осевые и центробежные моменты инерции сечения относительно центральных осей.

3. Определить положение главных центральных осей инерции сечения.

4. Вычислить главные центральные моменты инерции сечения.

 

Решение.

Вычерчиваем сечение в масштабе на листе чертежной или миллиметровой бумаги. Обозначим отдельные элементы: I  - двутавр; II – пластина; III – неравнобокий уголок (рис. 2). Затем проводим центральные оси каждого сечения X₁, Y₁;  X₂, Y₂ и X₃, Y₃.

Из сортамента выписываем все необходимые для расчета данные:

1. Двутавр №20 (ГОСТ  8239 – 89).

Как видим из чертежа (рис.2), двутавр расположен горизонтально, а в сортаменте – вертикально. По этой причине принимаем осевые  моменты  инерции 115 см⁴,   1840 м⁴,

 b₁ = h = 20 см, h₁ = b = 10 см, где J_x, J_y, h и b – числовые данные из сортамента. Площадь поперечного сечения А₁ = 26,8 см².

2. Пластина (прямоугольник): b₂ = 16 см; h₂ = 2 см.

см².

  

3. Уголок неравнобокий 100х63х6 мм (ГОСТ – 8510 – 86):

А₃ = 9,58 см³; = 98,3 см⁴;  = 30,6 см⁴;  = 18,2 см⁴;

х₀ = 1,42 см;   у₀ = 3,23 см;   = 0,393;   b₃ = 0,3 см;    h₃ = 10 см.

                                                                             Рис.2

 

1. Определение центра тяжести сечения. Выбираем в качестве вспомогательных осей – оси уголка х₃, у₃. Определяем относительно этих осей координаты центров тяжести сечений:

- для двутавра: х₁ = b₁/2 – х₀ = 20/2 – 1,42 = 8,58 см;

                            у₁ = у₀ + h₂/2+h₁/2 = 3,23 + 2/2+11/2 = 9,73 см;

- для пластины: х₂ = b₂/2  – х₀ = 24/2– 1,42 = 10,58 см;

                              у₂ = у₀ + h₂/2 = 3,23 +2/2 = 4,23 см;

- для уголка: х₃ = 0;  у₃ = 0.

Вычисляем координаты центра тяжести составного сечения по формулам:

 

 

Откладываем от вспомогательных осей х₃, у₃ координаты центра тяжести х_С, у_С и через полученную точку С проводим центральные оси  Х_С и Y_С параллельно вспомогательным осям.

2. Вычисление осевых (, ) и центробежного () моментов инерции сечения относительно центральных осей (X_С , Y_С). Применим формулы для вычисления моментов инерции составного сечения при параллельном переносе осей:

    = (115 + 4,23²26,8) + (16 + (-1,27)²48) + (98,3 + (-5,50)²9,58) =594 + 93,4 + 388 = 1075 см²,

где n₁, n₂ и n₃ – расстояния от центральной оси Х_С до осей х₁, х₂ и х₃, соответственно. Т.е. имеем:

n₁ = у₁ – у_С = 9,73 – 5,50 = 4,23 см;

n₂ = -(у_С – у₂) = -(5,50 – 4,23) = -1,27 см;

n₃ = - у_С = -5,50 см.

= (1840 + (-0,16)²26,8) + (2304 + 2,04²48) + (30,6 + (-8,74)²9,58) = 1841 + 2504 + 762 = 5107 см⁴,

где m₁, m₂ и m₃ – расстояние от центральной оси Y_С до осей у₁, у₂ и у₃, соответственно. Т.е. имеем:

m₁ = -(х_С – х₁) = -(8,74 – 8,58) = -0,16 см;

m₂ = х₂ – х_С = 10,58 – 8,74 = 2,04 см;

m₃ = -х_С = -8,74 см.

=(0 + 4,23(-0,16)26,8) + (0 + (-1,27)2,0448) + (31,5 + (-5,50)(-8,74)9,58) = -18,1 – 124,3 + 400 = 318 см⁴.

При вычислении центробежного момента инерции  следует учесть, что для симметричных сечений (двутавр, швеллер, пластина) центробежные моменты инерции относительно их собственных центральных осей равны нулю, т.к. оси симметрии являются главными осями. Тогда ,  .

Для неравнобокого уголка ось U₃ и ось V₃, проведенная нами через центр тяжести О₃ перпендикулярно первой оси, являются главными центральными осями уголка (см. рис.2). Следовательно, центробежный момент инерции уголка относительно этих осей равен нулю.

Оси х₃, у₃ не являются главными центральными осями. Поэтому . Для его вычисления воспользуемся известной формулой:

При этом для вычисления неизвестного главного момента инерции воспользуемся зависимостью:

Для определения угла  из сортамента имеем . Тогда .

Угол  в данном случае положителен, т.к. поворот главных центральных осей V₃, U₃ до совмещения их с осями х₃, у₃ выполнен против часовой стрелки (см. рис.2).

Для определения знака центробежного момента инерции для равнобоких и неравнобоких уголков в зависимости от их положения удобно пользоваться также данными рис.3.

                              Рис.3

Рис.2.3.

3. Определение положения главных центральных осей инерции.

Определяем угол  по формуле:                     

Рисунок 3

Откладываем от оси X_С угол  против часовой стрелки и проводим взаимно перпендикулярно главные оси для составного сечения U и V, соответственно.

4. Вычисление главных центральных моментов инерции. Для их вычисления используем формулу:

 

 

J_max = 5104 см⁴; J_min = 1050 см⁴.

Т.к. , то , а .

Для проверки правильности расчетов воспользуемся формулой для вычисления центробежного момента инерции. Вычислим его относительно главных центральных осей U и V (J_UV = 0):

где ;   

Ошибка в инженерных расчетах не должна превышать . Проверяем расчеты по формуле:

 

Пример 10.

Для составного поперечного сечения стержня, состоящего из равнобокого уголка № 7 с толщиной стенки 8 мм, швеллера №22 и полосы 180х20 мм (см. рис.1), требуется найти положение центра тяжести сечения, направление главных центральных осей инерции u и v, а также вычислить главные центральные моменты инерции I_max иI_min.

                                                                                                          Рис.1

Решение.

1. Определяем координаты центра тяжести поперечного сечения.

Размеры и геометрические характеристики уголка и швеллера устанавливаем по сортаментам. Вычерчиваем сечение в масштабе (см. рис. 1). Выбираем оси сравненияx и y, располагая их по контуру швеллера. Именно в этих осях мы и будем определять положение центра тяжести всего сечения. Для каждого элемента сечения (уголка, швеллера и полосы) проводим собственные центральные оси  (), параллельные выбранным осям сравнения x и y.

Координаты центра тяжести всего поперечного сечения (точка С), состоящего из трех элементов (уголка – 1, швеллера – 2 и полосы – 3), вычисляются по формулам:

где  и  – статические моменты соответствующего элемента относительно осей сравнения;  – площадь элемента;  и  – координаты центра тяжести элемента  в осях сравнения. Вычисления производим в табличной форме (таблица 1).

 

Таблица 1. Определение координат центра тяжести поперечного сечения

Номер элемента	Наименование элемента	Площадь элемента , см2	Координаты центра тяжести элемента		Статические моменты элемента относительно осей сравнения  и
			, см	, см	, см3	, см3
1	Уголок	10,67	-2,02	17,02	-21,55	181,60
2	Швеллер	26,70	2,21	11,00	59,01	293,70
3	Полоса	36,00	9,00	-1,00	324,00	-36,00
	ВСЕ СЕЧЕНИЕ	73,37			361,46	439,30

 

Координаты центра тяжести поперечного сечения (точка С) в осях сравнения x, y:

 см;    см.

По найденным значениям  и  отмечаем на чертеже центр тяжести всего сечения точку С (см. рисунок 1) и проводим центральные оси  и .

Заметим, что центр тяжести всей фигуры должен располагаться внутри треугольника, вершинами которого являются центры тяжести элементов поперечного сечения.

2. Вычисляем моменты инерции всего поперечного сечения относительно центральных осей  и .

Осевые и центробежный моменты инерции сечения относительно центральных осей определяются по следующим формулам:

Значения осевых моментов инерции уголка  и швеллера  относительно собственных центральных осей  и  определяем по сортаменту. Для полосы осевые моменты инерции соответственно равны:

 см⁴;    см⁴.

Центробежные моменты инерции швеллера  и полосы  равны нулю, поскольку их собственные центральные оси являются осями симметрии.

Центробежный момент инерции уголка  относительно собственных центральных осей  и  вычисляется по формуле

,

где  и – максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что  см⁴, а  см⁴.

Центробежный момент инерции уголка не равен нулю, поскольку оси  и  не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей  и  на угол 45⁰).

Знак центробежного момента инерции уголка (как, впрочем, и для любой другой фигуры) зависит от направления координатных осей. Он легко определяется следующим образом. Согласно определению, центробежный момент инерции фигуры равен интегралу, в котором элементарная площадка  умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,

 см⁴.

Теперь определяем координаты центров тяжести отдельных элементов C_i в центральных осях  и :

для уголка

 см;

 см;

для швеллера

 см;

 см;

для полосы

 см;

 см.

Дальнейшие вычисления моментов инерции всего поперечного сечения относительно центральных осей  и производим в табличной форме (таблица 2).

Таблица 2. Определение моментов инерции сечения относительно центральных осей  и 

Номер элемента	Наименование элемента	Площадь элемента , см2	Моменты инерции относительно собственных центральных осей и			Координаты центра тяжести в осях  и
			, см4	, см4	, см4	, см	, см
1	Уголок	10,67	48,16	48,16	28,19	-6,95	11,03
2	Швеллер	26,70	2110,00	151,00	0	-2,72	5,01
3	Полоса	36,00	12,00	972,00	0	4,07	-6,99
	ВСЕ СЕЧЕНИЕ	73,37

 

Продолжение таблицы 2

Наименование элемента	"Переносные" моменты инерции, см4			Моменты инерции относительно центральных осей  и , см4
Уголок	515,39	1298,12	-817,95	1346,28	563,55	-789,76
Швеллер	197,54	670,17	-363,85	2780,17	348,54	-363,85
Полоса	596,34	1758,96	-1024,17	1770,96	1568,34	-1024,17
ВСЕ СЕЧЕНИЕ				5897,41	2480,43	-2177,78

 

После округления вычисленных значений моментов инерции до трех значащих цифр, окончательно, получим

 см⁴;    см⁴;    см⁴.  

3. Определяем положение главных центральных осей инерции u и v.

Угол наклона главных центральных осей u и v к центральным осям  и  соответственно определяем из следующей формулы:

_.

Отсюда находим, что  и .

Откладываем положительное значение угла  от оси  против хода часовой стрелки и проводим главные центральные оси u и v (см. рисунок 1).

Ось, относительно которой момент инерции максимален, составляет меньший угол с той из центральных осей  или , относительно которой осевой момент больше. Поскольку  см⁴  больше, чем  см⁴, ось u является осью относительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.

4. Вычисляем значения главных центральных моментов инерции  и  для заданного поперечного сечения.

Значения главных центральных моментов инерции всей фигуры определяются по формуле

.

Тогда

см⁴;

 см⁴;     см⁴.

Контролем правильности последних вычислений может служить следующее условие:

.

Имеем

,     .

 

Пример 11.

Исходные данные.

Сложное сечение состоит из двух составляющих: 1 – швеллер № 20, 2 – прямоугольник с размерами h₂ = 1 см, b₂ = 12 см. Ось Y проходит через центр тяжести обоих составляющих (рис. а).

Требуется:

1. Привести геометрические характеристики простых составляющих сечения относительно их собственных центральных осей.

2. Вычертить сечение в масштабе с указанием основных размеров в числах и обозначением центральных осей простых составляющих сечения, параллельных вспомогательным осям.

3. Определить координаты центра тяжести всего сечения и построить на чертеже главные центральные оси, параллельные вспомогательным осям.

4. Выполнить проверку правильности выполнения третьего пункта путём вычисления статического момента всего сечения относительно общих центральных осей.

5. Определить значения главных центральных моментов инерции сечения.

6. Определить значения осевых моментов сопротивления (W_X, W_Y).

 

 

Решение.

1. Геометрические характеристики швеллера относительно его собственных центральных осей (рис. б) согласно ГОСТ 8240-72 следующие:

площадь A₁ = 23,4 см²,

высота сечения h₁ = 20 см,

моменты инерции , ,

абсцисса центра тяжести швеллера .

(ГОСТ прокатных профилей есть в приложениях всех литературных источников, приведённых в списке литературы).

Здесь и далее индекс в нижнем правом углу означает номер простой составляющей сечения. Например, швеллер, согласно принятой в задаче нумерации, имеет номер 1.

Геометрические характеристики прямоугольника относительно его собственных центральных осей (рис. в) следующие:

- площадь ,

- моменты инерции относительно собственных центральных осей

, .

2. Построение сечения в масштабе (см. рисунок 1, а).

3. Определение координаты центра тяжести сечения.

- Строим вспомогательную систему координат. В качестве вспомогательной системы координат выбираем центральные оси швеллера  и .

- Определяем координаты центра тяжести сечения относительно вспомогательной системы координат. Для рассматриваемого сечения необходимо вычислить только одну координату , так как другая координата  известна. Поскольку центр тяжести всего сечения должен лежать на прямой, соединяющей центры тяжести простых составляющих (это правило действительно для сечений, состоящих их двух частей), то в нашем случае центр тяжести лежит на оси  (см. рисунок 1, а), а значит координата .

Координата центра тяжести (к. ц. т.) сечения  определяется по формуле:

,

где А – площадь всего сечения;  - статический момент всего сечения относительно оси . Для рассматриваемого примера статический момент сечения следует обозначить, как , так как  определяется относительно оси .

Рассматриваемое сечение сложное. Для определения статического момента сложного сечения существует формула:   

,

где n – число простых составляющих сложного сечения;  - статический момент i –й составляющей сложного сечения; ,  - координата центра тяжести и площадь i –й составляющей сложного сечения. Применительно к нашей задаче формула примет следующий вид:

.

Так как координата y в прямоугольной системе координат представляет собой кратчайшее расстояние (перпендикуляр) от центра тяжести соответствующей фигуры до оси X, то:

, ;

 и  определены в пункте I. Подставим в формулу полученные значения:

.

Площадь сложного сечения . Тогда для рассматриваемого случая:

.

Следовательно, .

Для случая, когда неизвестной является координата , задача решается аналогично с учётом соответствующих изменений.

- Показываем на чертеже центральные оси всего сечения X_C и Y_C. Причём эти оси строим параллельно вспомогательным осям, как показано на рис. а.

4. Проводим проверку правильности определения центра тяжести сечения.

В основе проверки лежит положение о том, что статические моменты сечения относительно центральных осей равны нулю. Значит, в нашем случае следует вычислить статические моменты сечения относительно полученных центральных осей X_C и Y_C, при этом координаты ц. т. простых составляющих относительно этих осей:

,       ;

,

.

Статические моменты сечения относительно осей X_C и Y_C:

.

Иными словами, координаты ц. т. всего сечения вычислены правильно.

5. Определяем главные центральные моменты инерции сечения.

- Вычисляем центробежный момент инерции всего сечения.

Ось  - центральная ось всего сечения и ,  - центральные оси простых составляющих – совпадают. Оси  и  - главные оси швеллера, значит  центробежный момент инерции швеллера относительно них . Оси  и  - главные оси прямоугольника (так как оси  и  - оси симметрии прямоугольника), то есть . В этом случае центробежный момент инерции всего сечения в соответствии с формулой изменения центробежных моментов инерции при параллельном переносе осей (см. теорию):

.

- Находим главные оси всего сечения.

Так как центробежный момент инерции сечения относительно главных осей равен нулю, то в нашем случае оси X_C и Y_C  - главные оси инерции всего сечения.

- Вычисляем главные центральные моменты инерции всего сечения.

Поскольку главными центральными моментами инерции являются моменты инерции относительно главных центральных осей, то вычисления моментов инерции будем производить относительно осей X_C и Y_C.

Воспользовавшись формулой определения осевых моментов инерции сложного сечения и формулой перехода между параллельными осями для осевых моментов инерции (см. теорию), получим

6. Определяем значения осевых моментов сопротивления.

Осевые моменты сопротивления в нашем случае вычисляются по формулам

;       ,

где x_max и y_max - расстояния от соответствующих осей до наиболее удалённых точек сечения (см. рис. а).

Здесь: ;

;

.

Тогда:  ;

;

.

 

Пример 12.

Рассмотрим сечение, состоящее из прокатных профилей (см. рис.1).

                                                              Рис.1

 

Решение.

Вычертив в масштабе сечение, нумеруем элементы, с указанием их размерных характеристик – номера двутавра и швеллера, размеры перьев и толщину уголков, высоту и толщину листа.

Проставляем начальные размеры, необходимые для определения положения элементов в сечении – ширина полки двутавра, расстояния до центров тяжестей уголка и швеллера от их граней (из таблицы ГОСТ).

Принимаем положение начальных осей сечения. Пусть горизонтальная ось  q  проходит через центр тяжести вертикального листа, а вертикальная   р – через центр тяжести двутавра. Указываем на чертеже положение начальных осей.

Рассчитываем и указываем на чертеже координаты центров тяжести элементов относительно начальных осей.

р_с = -1,02 см;     q_c = 14,76 см.

Определяем осевые  ,   и центробежный    моменты инерции элементов относительно собственных центральных осей параллельных начальным осям сечения. Осевые моменты инерции двутавра, швеллера и уголков принимается из таблиц ГОСТ, с учетом положения их осей. Осевые моменты инерции листа (прямоугольное сечение) рассчитываются по формуле  , где  b  - размер параллельный, h – размер перпендикулярный оси, относительно которой вычисляется момент инерции.

Для вертикального листа 601,2 (см) (элемент № 2) имеем:

см4;      см4.

Центробежный момент инерции в рассматриваемом сечении отличен от нуля только у неравнобокого уголка (элемент № 3) . Согласно ГОСТ 8210-86 для неравнобокого уголка - 2012,51   см⁴;   см ⁴; . Согласно рис. 2 угол .

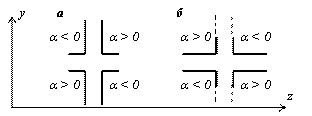
Рис.2. К определению знака угла  положения главных осей уголков

 

Тогда по формуле  получим  и по формуле : см⁴.

Все данные по элементам сечения - моменты инерции относительно центральных осей элементов и координаты центров тяжестей заносятся в таблицу (см. табл.).Табличная форма позволяет удобно контролировать правильность подготовки исходных данных, от которых зависит корректность дальнейших расчетов.                

                                                                                                                                                                  

№ п/п	Тип элемента	А , см2	, cм4	, cм4	, cм4	pc , см	qc , см	yc , см	zc , см
1.	I  № 45	84,7	27696	808	0	22,0	0	23,02	-14,76
2.	|  601,2	72,0	8,64	21600	0	0	23,10	1,02	8,34
3.	2012,51,2	37,9	482	1568	503	-23,46	19,67	-22,44	4,91
4.	[  № 30	40,5	327	5810	0	-30,00	26,22	- 28,98	11,46
		235,1	28510	29790	503

 

Вычисляем координаты центра тяжести сечения относительно начальных осей:

 см;

 см. 

7.  Определяем координаты центров тяжести элементов сечения относительно центральных осей:

            ;                                   ;     

см;                см;

см;                       см;

см;        см;

см;            см.

Координаты центров тяжестей элементов записываем в таблицу.                           

Проводим проверку правильности вычисления координат центров тяжести сечения и его элементов:

;       ;

=.

Относительная невязка:

;

.

Определяем осевые,  центробежный и полярный моменты инерции сечения относительно центральных осей:

см ⁴;

 

см ⁴;

см⁴; 

 см⁴.            

Замечание. Результаты расчетов округлялись до четырех значащих цифр.

Определяем положение главных осей:

;  ;    .

Определяем главные моменты инерции:

(см⁴);

см⁴;      см⁴;

или, в соответствии с формулами:

;     ;       

;  

см ⁴;          см ⁴;  

Из расчета видно, что , т.е. максимальный момент инерции возникает относительно оси  v, которая ближе к оси  z,  оси с наибольшим значением момента инерции  .

Сумма главных моментов инерции должна быть равна сумме осевых моментов инерции, или полярному моменту инерции

.

Определение главных моментов инерции и положения главных осей с помощью круга Мора  (рис. 3).

                                                       Рис.3

 

Определяем из чертежа в масштабе главные моменты инерции и угол   поворота главных осей (с помощью транспортира):

см⁴;     см⁴;     .

Графический метод показал хорошее совпадение с результатами аналитического расчета.

 

Пример 13.

Для сечения, составленного из швеллера №20а, равнобокого уголка (80х80х8)10^-9 м³ и полосы (180х10)10^-6 м² (см. рис.) требу­ется:

1. Найти общую площадь сечения;

2. Определить центр тяжести составного сечения;

3. Определить осевые и центробежный моменты инерции сече­ния относительно осей, проходящих через его центр тяжести;

4. Найти положение главных центральных осей инерции;

5. Определить величины главных центральных моментов инер­ции сечения и проверить правильность их вычисления;

6. Вычислить величины главных радиусов инерции.

 

Решение.

1. Определение общей площади составного сече­ния. Общая площадь составного сечения определяется по фор­муле:

,     А = (25,2 + 12,3 + 18)10^-4 = 55,510^-4 м².

2. Определить центр тяжести составного сече­ния. В качестве вспомогательных осей для определения положения центра тяжести примем горизонтальную и вертикальную оси x_шв и y_шв , проходящие через центр тяжести швеллера. Статические моменты площади всего сечения относительно этих осей будут равны:

Координаты центра тяжести вычисляем по формулам:

м,    м.

3. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих че­рез его центр тяжести. Для определения указанных момен­тов инерции составного сечения воспользуемся формулами, выра­жающими зависимость между моментами инерции относительно параллельных осей:

                                       (1)

                                        (2)

                       (3)

В этих формулах расстояние между осями, проходящими через центр тяжести составного сечения, и осями, проходящими через центры тяжести каждой составной части фигуры, а и b (см. рис.), в рассматриваемом случае будут равны:

 м,       м;

м;

м.

Подставив числовые значения величин в формулы (1) и (2), получим:

= [1670 + 25,2(1,7)² + 73,4 + 12,3(9,43)² + 1,5 + 18(8,8)²]10^8 = 4305,410^-8 м⁴.

= [139 + 25,2(1,42)² + 73,4 + 12,3(3,13)² + 486 +18(0,14)²]10^8 = 870,110^-8 м⁴.

При вычислении центробежного момента инерции составного сечения следует иметь в виду, что  и  равны 0, так как швеллер и полоса имеют оси симметрии, а

,

где      угол между осью x и главной осью  уголка. Этот угол может быть положительным или отрицатель­ным. В нашем примере  = +45, поэтому:

м⁴.

Далее, подставив числовые значения в формулу (3), получим величину центробежного момента инерции составного сечения:

= [0 + 25,2  (1,7)  1,42 + 42,85 + 12,3  (9,43) (3,13)  + 0 + 18  8,8  0,14] 10^8 = 367,210^-8 м⁴.

4. Найти положение главных центральных осей инерции. Угол наклона главных осей инерции, проходящих через центр тяжести составного сечения, к центральным осям инерции  и  определим по формуле:

        .

Так как угол  получился отрицательным, то для отыскания по­ложения главной оси максимального момента инерции u следует ось , осевой момент инерции относительно которой имеет наи­большее значение, повернуть на угол  по ходу часовой стрелки. Вторая ось минимального момента инерции v будет перпендику­лярна оси u.

5. Определить величины главных центральных мо­ментов инерции сечения и проверить правильность их вычисления. Величины главных центральных моментов инерции составного сечения вычисляем по формуле:

Для контроля правильности вычисления величины моментов инерции составного сечения производим проверки.

1ая проверка: ;

I_max + I_min = (4344,55 + 830,95)10^-8 = (5175,5)10^-8 м⁴;

= (4305,4 + 870,1)10^-8 = (5175,5)10^-8 м⁴.

2ая проверка: ;

4344,55 10^-8 > 4305,410^-8 > 870,110^-8 > 830,9510^-8 м⁴.

Проверки удовлетворяются, что говорит о правильности вычис­ления моментов инерции составного сечения.

6. Вычислить величины главных радиусов инерции. Величины главных радиусов инерции вычисляем по известным формулам:

 

Пример 14.

Для составного сечения, состоящего из швеллера и уголка (рис.1) требуется:

1) определить положение центра тяжести;

2) найти величины осевых и центробежных моментов инерции относительно центральных осей;

3) определить направления главных центральных осей;

4) найти величины моментов инерции относительно главных нейтральных осей;

5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.

                                                             Рис.1

 

Решение.

Выпишем данные из сортамента.

Уголок равнобокий № 14 (10)

 

h₁ = b₁ = 14 cм, F₁ = 27,3 см²,

Z₀₁ = 3,82 см,

см⁴.

 см⁴,     см⁴.

см⁴.

 где угол  взят отрицательным, так как ось х₀ для совпадения с осью х₁ поворачивается по часовой стрелке, .

 

Швеллер №20

 

h₂ = 20 см, b₂ = 7,6 см,

Z₀₁ = 2,07 см,

F₂ = 23,4 см², =1520 см⁴,

=87,8 см⁴, =0.

1. Определим положение центра тяжести составного сечения.

Для этого следует начертить профиль составного сечения в масштабе 1:2, провести координатные оси .         

Выберем координатную систему х-у так, чтобы составной профиль оказался в первой четверти.

Координаты центра тяжести определим из выражений

,    .

где S_х, S_у - статические моменты составного сечения относительно осей х и у.

;     ;

 см;

 см;

 см;

см;

см³;

см³;

 см²;

см, см.

По координатам х_с и у_с найдем положение центра тяжести сечения. Через т.С проведем оси х_с-у_с - центральные оси.

2. Вычислим величины осевых и центробежных моментов сечения относительно центральных осей х_с -у_с:

;

;

.

где

см;

см;

см;

см;

см⁴;

см⁴;

см⁴.

3. Определим направление главных центральных осей.

Главные оси х₀ -у₀ проходят через центр тяжести т.С и повернуть относительно центральных осей на угол , определяемый из формулы

 ,   ,     .

T.к. , то оси х₀ - у₀ получаются поворотом от осей х_с - у_с против часовой стрелки.

4. Найдем величины моментов инерции относительно главных центральных осей

см⁴.

см⁴.

При правильно выполненных вычислениях должно выполняться равенство

2513,26+1036,92=2835+715,18

.

 

Пример 15.

Найти положение главных центральных осей инерции и значение главных моментов инерции для сечения состоящего из равнобокого уголка и двутавра (см. рис.1). Вычертить сечение в масштабе 1:2 и указать на нём все размеры в числах и все оси, если дано: уголок 90х7, двутавр №22.

 

Решение.

Из сортамента выбираем необходимые данные.

Для уголка равнобокого 90х7 по ГОСТ 8509-89 b = 90 мм, d = 7 мм, z₀ = 2,47 см, F₁=12,28 см²,  I_x1 = I_y1 = 94,3 см⁴, I_max = 149,67 см⁴, I_min = 38,94 см⁴.

Для двутавра по ГОСТ 8239-89 h = 220 мм, b = 110 мм, d =5,7 мм, F₂ = 30,6 см², I_x2 = 2550 см⁴, I_Y2 = 157 см⁴.

1. Проводим вспомогательную систему осей координат (Х, Y). Начало координат целесообразно расположить в центре тяжести какой-либо из фигур, напримердвутавра (чтобы сократить объём вычислений). Определяем координаты центра тяжести С всей фигуры в системе осей Х и Y:

где

Через центр тяжести С (рисунок 3) проводим центральные оси Х_С и Y_C параллельно проведённым ранее собственным осям уголка и двутавра (Х₁, Y₁, Х₂, Y₂).

В системе координат центральных осей Х_С и Y_C координаты центров тяжести уголка и двутавра определяем из выражений

Данные сводим в таблицу 1.

Таблица 1

Точка	хi, см	yi, см	ai, см	bi, см
О1	- 2,47	13,47	9,61	- 1,76
О2	0	0	- 3,86	0,707

2. Вычисляем осевые и центробежный моменты инерции относительно центральных осей X_с, Y_с:

Для равнобокого уголка

Для двутавра 

Знак центробежного момента инерции уголка определяем по следующему правилу (см. рис.2):

                                                                                                 Рис.2

3. Находим угол  наклона главных центральных осей U и V относительно центральных осей Х_С и Y_C:

Поскольку угол  положительный, главная центральная ось U откладывается относительно оси Х_С против часовой стрелки, а так как I_xc >I_yc, то ось U является осью, относительно которой момент инерции будет максимальным.

4. Вычисляем главные моменты инерции

5. Проверка

 

Задачи для самостоятельного решения

Задача № 1         

Как изменятся площадь и момент инерции J_у сечения трубчатой балки, изображенной на рис. а), если заменить одно отверстие диаметром 200 мм—двумя, диаметром каждое по 100 мм, расположенными, как показано на рис. б)?

Ответ: Площадь увеличится на 38,6%, а момент инерции уменьшится на 2%.

 

Задача № 2

Сечение балки состоит из двух швеллеров № 33b, усиленных двумя листами 14х300 мм, приклепанных к полкам. Определить момент инерции сечения относительно центральной оси у с учетом ослабления его заклепочными отверстиями d = 23 мм (см. рисунок) и оценить ослабление сечения (в процентах к моменту инерции неослабленного сечения).

Ответ: J_х =35200 см⁴;  =16,5%.

 

Задача № 3

Поперечное сечение раскоса навесного плуга изготовлено из двух равнополочных уголков размером 63х63х5 (см. рис.). Определить моменты инерции относительно центральных осей х_С и у_С.

Ответ. Моменты инерции: Jx_С = Jy_С = 70,5 см⁴.

 

Задача № 4

Поперечное сечение стержня (см. рис.) состоит из двутавра № 55 (ГОСТ 8239-72), швеллера № 18 (ГОСТ 8240-72). Определить расстояние х_С от центра тяжести двутавра с₁до центра тяжести с всего сечения.

Ответ. Искомое расстояние х_С = 44 мм.

 

Задача № 5

На рис. показано сечение поперечины прицепного устройства пропашного трактора. Определить моменты инерции сечения относительно центральных осей х_С  и у_С.

Ответ. Моменты инерции: Jx_С  = 14,7 см⁴; Jy_С = 119,6 см⁴.

 

Задача № 6

Определить моменты инерции относительно центральных осей х_С и у_С сечения кронштейна растяжек пропашного трактора (см. рис.).

Ответ. Моменты инерции: Jx_С  = 8,0 см⁴;  Jy_С  =30,3 см⁴.

 

Задача № 7

Определить моменты инерции относительно центральных осей х_С и у_С двух различных сечений рамы трактора, показанных на рис. а, б.

Ответ. Моменты инерции (в табл.).

Сечение	а	б
JхС, см4	324	1604
JуС, см4	932	9271

 

Задача № 8

Определить моменты инерции относительно центральных осей х_С и у_С сечения опорной поперечины рамы тракторного прицепа (см. рис.).

Ответ. Моменты инерции: J_хс,= 830 см⁴; J_ус = 527 см⁴.

 

Задача № 9

Определить центр тяжести поперечного сечения, изображенного на рисунке.

Ответ: х_с = 10,57 см;  у_с = 9,43 см. (Центр тяжести С поперечного сечения должен лежать на оси симметрии поперечного сечения).

 

Задача №22

Определить положение центра тяжести составного сечения, показанного на рис. 1.

Вычислить статические моменты S_x, S_y сложного составного сечения (рис.2). Определить площадь этого сечения и найти координаты его центра тяжести.

Решение к рис 2. Предлагается следующий порядок решения.

Если поперечное сечение не содержит осей симметрии, то случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте. Каждому прокатному профилю присваивается порядковый номер.

Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i – го профиля относительно случайных осей х, у; А_i – площадь сечения i – го профиля,  А – площадь поперечного сечения всего составного сечения, n – число профилей.

Затем вычисляются статические моменты всего сечения по формулам  , а по формулам находятся координаты центра тяжести.

Следуя предложенной методике, выпишем (рис. 2): А₁ = 6,36 см²; А₂ = 23,4 см²; А₃ = 26,8 см²; А = 56,56 см²; х₁ = 3,87 см; х₂ = 7,07 см; х₃ = =17,6 см; у₁ = 17,4 см;  у₂ = 10 см;  у₃ = 10 см.

По формулам  находим

И наконец, с помощью формул  определяем координаты центра тяжести всего сечения:

Для проверки полученных результатов рекомендуем самостоятельно определить координаты центра тяжести составного сечения относительно осей p, q (рис. 2).

Ответ к рис.1: x_c = 11,7 см;  y_c = 10,83 см.

Ответ к рис.2: x_c = 0;  y_c = 10,83 см.

 

Задача №23

Вычислить координаты центра тяжести составного сечения, состоящего из швеллера и уголка (рис. 1)

Вычислить координаты центра тяжести сложного составного сечения, изображенного на рис. 2.

Ответ к рис 1: х_с = 7,74 см; у_с = 6,76 см.

Ответ к рис 2: х_с  = 0;  у_с  = 9,23 см.

 

Задача №31

Найти положение центра тяжести поперечного сечения железобетонной балки (см. рис.). Вычислить главные моменты инерции относительно главных осей х_с, у.

Указания. Для расчета использовать материалы предыдущего примера, в котором определены главные моменты инерции сечения в виде равнобокой трапеции. В рассматриваемом случае необходимо принять a = 20 см, h = 20 см, b = 40 см, тогда для трапециевидной части поперечного сечения балки будем иметь

A₁=600 см²; 

Ответ: y_c = –1,7 см; I_y = 116667 см⁴.

 

Задача №33

Найти положение центра тяжести площади поперечного сечения, представленного на рис. 1. Определить главные моменты инерции этого сечения.

Вычислить главные моменты инерции для сечения, показанного на рис. 2.

Вычислить главные моменты инерции поперечного сечения круглого бревна диаметром d и прямоугольного сечения бруса с b= d/2, выполненного из этого бревна (рис. 3). Найти высоту h прямоугольного сечения бруса.

Ответ к рис.1: 

Ответ к рис.2: I_y = I_max = 1172,62 см⁴; I_min = 122,11 см⁴.

Ответ к рис.3:  I_x = I_y = 0,049087d⁴ (для круглого поперечного сечения), I_x = 0,02706d⁴; I_y = 0,009021d⁴ (для прямоугольного поперечного сечения).

 

Задача №34

Найти положение центра тяжести С и вычислить главные моменты инерции поперечного сечения участка стены таврового сечения (см. рис. 1). Кладка выполнена из глиняного кирпича пластического прессования на растворе.

Найти положение центра тяжести и вычислить момент инерции для поперечного сечения, изображенного на рис. 2.

Определить главные моменты инерции поперечного сечения, показанного на рис. 3.

Ответ к рис.1: х_с = 0,44 м; 

Ответ к рис.2: 

Ответ к рис.3: I_x = 26086 см⁴;  I_y = 3898 см⁴.

 

Задача №35

Вычислить главные моменты инерции для составного поперечного сечения, изображенного на рис.1.

Вычислить главные моменты инерции для составного поперечного сечения, представленного на рис. 2. Найти положение главных осей инерции.

Ответ к рис.1: I_max = 5828,4 см⁴; I_min = I_у = 2301,7 см⁴.

Ответ к рис.2: х_с = 11,7 см;  у_с = 10,83 см; = 0,4642; = 12^о27^/;   I_max = 3795 см⁴; I_min = 1981 см⁴;   

 

Задачи №36 – 44

Найти координаты центра тяжести и вычислить главные моменты инерции для составных поперечных сечений, показанных на рис. 1 – 9.

Ответ к рис. 1: х_с = 0; у_с = 3,8 см; 

Ответ к рис. 2: х_с = 0; у_с = 7,05 см; 

Ответ к рис. 3: х_с = 0; у_с = –4,54 см;  

Ответ к рис. 4: х_с = 0; у_с = 2 см;  

Ответ к рис. 5: х_с = 0;  у_с = 3,3 см; 

Ответ к рис. 6: х_с = 0;  у_с = 6,6 см; 

Ответ к рис. 7: х_с = 0;  у_с = 0;  I_x = 7411 см⁴;    I_y = 622,5 см⁴.

Ответ к рис. 8:   х_с = 0;  у_с = –1,3 см;  I_min = 524 см⁴;   I_y = I_max = 1818 см⁴.

Ответ к рис. 9:   х_с = у_с = 0;     I_x = 5290 см⁴;    I_y = 537,6 см⁴.

Лекция 4 (продолжение). Примеры решения задач по геометрическим характеристикам плоских сечений и задачи для самостоятельного решения

 

Геометрические характеристики простых сечений

Пример 1.

Определить положение центра тяжести полукруга (см. рис.).

Решение.

Направим ось y по оси симметрии полукруга, а ось z совместим с его основанием. В этом случае z_c=0, надо определить только координату y_c. Подсчитаем S_zнепосредственным интегрированием по площади полукруга:

.

Далее по формуле находим расстояние центра тяжести от основания полукруга:

.

 

Пример 2.

Для прямоугольного поперечного сечения определить моменты инерции относительно осей геометрической симметрии  и осей, совпадающих со сторонами прямоугольника  (см. рис.).

Решение.

Оси x, y являются главными центральными для прямоугольного поперечного сечения, так как они совпадают с осями геометрической симметрии. Оси x⁰, y⁰ − в данном случае будут вспомогательными. Для определения осевого момента инерции J_x выделим на расстоянии y полоску шириной B и толщиной dy, следовательно dF=Bdy, тогда

 

Теперь рассмотрим на расстоянии x от оси y полоску шириной h и толщиной dx, в этом случае dF=hdy и момент инерции J_y будет равен

Центробежный момент инерции

где .

Моменты инерции относительно осей x⁰, y⁰, можно вычислить используя формулы переноса, полагая , тогда

 

Пример 3.

Определить геометрические характеристики относительно центральных и главных осей для сечения в виде прямоугольного треугольника, изображенного на рисунке.

Решение.

Отнесем треугольник к вспомогательной системе координат x⁰, y⁰. В качестве элементарной площади возьмем полоску на расстоянии y⁰ толщиной dy⁰ и переменной ширины b(y⁰) так, что

.

Из подобия треугольников нетрудно установить, что:

,

тогда .

Статический момент будет равен

По аналогии получим

Площадь треугольника

.

Координаты центра тяжести C определим по формулам:

Через точку C проводим центральные оси x, y параллельные осям 

Момент инерции  и аналогично  равны:

,

.

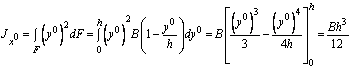Для определения момента инерции относительно центральной оси x воспользуемся формулой при параллельном переносе осей

.

Так как , то

  

Центробежный момент

,

где ; .

Интегрируя, получаем

 

Перейдя к центральным осям x и y, получим

.

Определение направлений главных осей:

.

Проводим главные центральные оси 1 и 2.

Если, например, , то имеем равнобедренный треугольник, для которого , , . Тогда:

.

 

Пример 4.

 Определить площадь и моменты инерции относительно главных центральных осей инерции круглого поперечного сечения диаметра  (см. рис.).

Решение.

Выберем оси x, y, которые для круглого сечения будут главными и центральными, так как являются осями геометрической симметрии. В качестве элементарной площади dF возьмем полоску на уровне y толщиной dy и шириной b(y), т.е. . Координаты точки A на контуре сечения, а также dy, b(y) равны:

.

Тогда элементарная площадь

.

Площадь круга

.

Моменты инерции относительно оси x

Такое значение имеет момент инерции относительно оси y. Следовательно, полярный момент инерции для круга

.

 

Пример 5.

 Определить положение центра тяжести и моменты инерции относительно главных центральных осей для поперечного сечения в виде полукруга (см. рис.).

 

Решение.

Проводим вспомогательные оси x⁰, y⁰ при этом учтем, что ось y⁰ является осью геометрической симметрии и будет одной из главных центральных осей инерции сечения − 1 (см. рис.). Вторая главная центральная ось будет проходить через центр тяжести сечения и перпендикулярно оси  y⁰.

Площадь полукруга .

Статический момент относительно вспомогательной оси x⁰ равен

,

где .

Координаты центра тяжести в осях x⁰, y⁰:

Через точку С с координатами ,   проводим вторую главную центральную ось инерции − 2 (см. рис.). Таким образом? положение главных центральных осей для заданного сечения − определено.

Моменты инерции полукруга относительно осей x⁰, y⁰ будут равны половине моментов инерции полного круга, найденных в предыдущей задаче:

.

Определим осевые моменты инерции сечения относительно главных центральных осей

 

Пример 6.

 Найти центробежный момент инерции для равнобокого уголка 125х125х10 (мм) относительно центральных осей x, y.

а)                                                б)                                               в)

 

Решение.

Из таблицы ГОСТа для уголка (рис. а) находим

J₁=571 мм⁴, J₂=149 мм⁴,  J₁₂=0,   =3,45 мм,  =-45⁰,  F=24,3 мм².

Центробежный момент

мм⁴.

Для уголка (рис. б) угол ,

мм⁴.

Для уголка (рис. в) угол ,

J_xy=211 мм⁴.

 

Пример 7.

Определить центробежный момент инерции неравнобокого уголка 160х100х10 относительно центральных осей, параллельных полкам (см. рис.).

 

Решение:

По  таблице  сортамента прокатной стали в соответствии с ГОСТ 8510-72 (СТ СЭВ 255-76) имеем = 204 cм⁴,    = 667 cм⁴,   I_u min = 121 cм⁴,    = 0,390.

Для определения центробежного момента инерции  воспользуемся формулами поворота осей (переход от главных осей  к данным )  

.

Угол в данном случае отрицателен, так как кратчайшее совмещение оси  с  происходит по часовой стрелке. Главный момент инерции задан в таблице сортамента,   а главный момент  определяем из соотношения     

,

откуда  = 204 + 667 – 121 = 750 см⁴.

Таким образом, центробежный момент уголка будет равен

= 0,5(121-750)(-0,677) = 213 см⁴.

 

Пример 8.

Определить центробежный момент инерции равнобокого уголка 100х100х10 относительно центральных осей, параллельных полкам (см. рис.).

 

Решение:

По таблице сортамента  прокатной  стали  в соответствии с ГОСТ 8509-72 (СТ СЭВ 104-74) имеем =284 см⁴, =74,1 см⁴,   =3,84 см,   =1,96 см.

Пользуясь формулой поворота, находим

,

см⁴.

 

Пример 9.

Определить центр тяжести треугольного поперечного сечения, показанного на рисунке.

Решение.

Поперечное сечение представляет собой равнобедренный треугольник, а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного сечения лежит на этой оси. 

Для нахождения центра тяжести используем формулу Запишем

                                 (а)

Из подобия треугольников  и  находим

 или  откуда  

Найденное значение b_y подставляем в формулу (а) для вычисления статического момента S_x:

В этом случае формула дает

На рисунке проводим линию у = у_с = h/3. Центр тяжести треугольного поперечного сечения будет лежать на пересечении проведенной линии и оси у. Координаты центра тяжести этого сечения: х = 0, у = h/3.

Ответ: x_c = 0, y_c = 4R/(3).

 

Пример 10.

Определить статические моменты S_x и S_y сложного поперечного сечения (см. рис.). Найти координаты его центра тяжести.

Решение.

Разбиваем сложное поперечное сечение на две простые фигуры: прямоугольное сечение с размерами  и площадью A₁ = h²/2, координаты центра тяжести (C₁) которого y_1c = h/2, x_1c = h/4 и прямоугольное сечение  с центром тяжести С₂ (y_2c = h/2, x_2c = 5h/16) и площадью A₂ = 9h²/32.

По формулам

 

вычисляем статические моменты всего сечения:

Площадь поперечного сечения всей конструкции А находим как разность площадей А₁ и А₂: А = А₁ – А₂ = 7h²/32. Подставляя полученные значения в формулы , находим координаты центра тяжести С всего сечения:

y_c = S_x/A = h/2;  x_c = S_y/A = 19h/112.

 

Пример 11.

Определить полярный момент инерции круглого поперечного сечения (см. рис.) относительно точки С.

      

Решение.

За элементарную площадку выберем кольцевую область вокруг центра С с внутренним радиусом ρ и шириной dρ. Определим площадь элементарной площадки . Затем результат подставляем в формулу :

 

Пример 12.

Определить осевые моменты инерции круглого сплошного поперечного сечения относительно произвольных центральных осей х, у (см. рис.).

Решение.

В примере 17 найдено, что . Однако для круглого сплошного сечения  I_x = I_y, поэтому формула  для этого сечения принимает вид: 2I_x = I_ρ, откуда находим

                    

 

Пример 13.  

Определить осевые моменты инерции I_x, I_y прямоугольного треугольника относительно случайных осей х, у (см. рис.). Вычислить положение центра тяжести. Найти значения осевых моментов инерции ,и центробежный момент инерции  относительно центральных осей х_с, у_с, проходящих через центр тяжести С. Определить расположение главных осей инерции поперечного сечения в форме сплошного прямоугольного треугольника.

Указания. Для нахождения центробежного момента инерции  можно использовать формулы  и  которые для рассматриваемого случая принимают вид:

Из подобия треугольников находим (см. рис.):  откуда  следовательно, площадь элементарной площадки dA будет

Горизонтальная координата х центра тяжести элементарной площадки dA определяется как x = b_y /2 =b (h – y)/(2h).

Подставим значения х и dA в формулу для определения I_xy:

Переходим к центральным осям х_с и у_с, для которых

Ответ:   

 

Пример 14.  

Определить расстояние а между элементами пакета, состоящего из трех досок размером , при условии равенства главных моментов инерции относительно осей х и у (см. рис.).

Решение.

Момент инерции всего сечения относительно оси х будет

При определении момента инерции сечения относительно оси у для двух крайних прямоугольников следует воспользоваться формулой так как ось у не является для них центральной и, следовательно, для всего пакета из трех досок будем иметь

По условию задачи I_x = I_y, или 17280 = 240a² + 2400a + 6750.

Решив полученное квадратное уравнение, найдем a = 3,3 см.

    

Пример 15.  

Сечение стержня представляющее собой фигуру, обладающую одной осью симметрии, показано на рис. 1. Требуется найти моменты инерции этой фигуры относительно главных центральных осей.

                   Рис.1

 

Решение.

Ось  – ось симметрии фигуры (рис. 1) является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату  по формуле . Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I , III и прямоугольник II (см. рис. 2). Площадь фигуры

Для определения статического момента выберем вспомогательную ось , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе :

Тогда по  

                                                          Рис.2

 

Откладываем эту координату и проводим через центр тяжести (точку С на рис. 2) главную центральную ось .

Найдем моменты инерции всей фигуры относительно осей  и , складывая (или вычитая) моменты инерции составляющих фигур:

;

.

Для определения момента инерции каждой из фигур I, II и Ш используем формулы изменения моментов инерций при параллельном переносе осей ,  . Моменты инерции прямоугольника II находим по формулам ;          ;  и треугольников I и Ш находим по формулам ; ;  относительно собственных центральных осей (см. рис. 2).

Тогда

 

В заключение вычислим радиусы инерции относительно главных центральных осей по формулам ,  и построим эллипс инерции.

             

Эллипс инерции показан на рис. 2.

 

Пример 16.

Для фигуры, показанной на рисунке определить главные моменты инерции и положение главных осей инерции.

 

Решение.

Разбиваем сложное сечение на простейшие геометрические фигуры

S₁ = 2000 мм², S₂ =1200 мм², S = 3200 мм².

Выбираем произвольные оси XOY.

Определяем положение центра тяжести сечения

Определяем статические моменты площади

мм³

мм³

Находим координаты центра тяжести

мм;

мм.

Проводим центральные оси X_cOY_c

мм,

мм,

мм,

мм.

Вычисляем моменты инерции Ix_c, Iy_c

мм⁴

6) Вычисляем центробежный момент инерции Ix_cy_c

Определяем положение главных осей инерции

Если I_x>I_y и , то угол  откладывается от оси Х_с против часовой стрелки.

7) Вычисляем главные моменты инерции I_max, I_min

 

Пример 17.

Определить положение центра тяжести сечения, приведенного на рис.1 (размеры даны в см).

Решение:

Разбиваем сечение на три прямоугольника и выбираем вспомогательные оси  uv (рис. 2).

                        Рис.1

 

Вычисления представим в виде следующей таблицы

Номер вычисления	Координаты, см		Площадь Аi, см2	Статические моменты, см3
	ui	vi		uiAi	viAi
1 2 3	11 9 5	1 8 15	12 24 20	132 216 100	12 192 300
			56	448	504

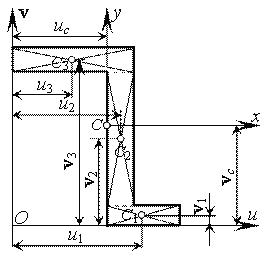
                                 Рис.2

 

Определяем координаты центра тяжести сечения:

 см,

 см.

 

Пример 18.

Для данного сечения определить моменты инерции относительно центральных осей x и y.

Решение:

Моменты инерции прямоугольников относительно собственных центральных осей определяем по формулам ,   . Пользуясь формулами перехода к параллельным осям, вычисляем искомые моменты инерции, представленные в нижеприведенной таблице.

 

Номер элемента	Координаты центра тяжести, см		Площадь Аi, см2	Моменты инерции площадей, см4
	xi	yi				Ixi			Iyi		xiyiAi	Ixiyi
1	3	-8	12	4	768	772	36	108	144	0	-288	-288
2	1	-1	24	288	24	312	8	24	32	0	024	-24
3	-3	6	20	6,7	720	727	167	180	347	0	-360	-360
				299	1512	1811	211	312	523	0	-672	-672

 

 

Задачи для самостоятельного решения

Задача № 1.

Определить осевые и полярный моменты инерции полого сечения рамы картофелеуборочной машины (см. рис.), если D = 96 мм, d = 69,5 мм.

Ответ. Моменты инерции: Jx_С = Jy_С  =108 см⁴; Jp =216 см⁴.

 

Задача № 2.        

Определить момент инерции относительно центральной оси y сечения, изображенного на рисунке. Размеры показаны в мм.

Ответ: J_х =3167 см⁴.

 

Задача № 3.

Найти моменты инерции полукруга относительно главных центральных осей инерции (см. рис.).

Ответ:  

 

Задача № 4.

Определить координату у_С центра тяжести несимметричного двутавра (см. рис.).

Ответ. Координата у_С  = 43,1 мм.

 

Задача № 5.

Определить моменты инерции относительно центральных осей х_С и у_С сечения передней оси автомобиля, которое показано на рис.

Ответ. Моменты инерции: J_xс =198 см⁴; J_yс =183 см⁴.

 

Задача № 6.

Для прямоугольника высотой h и шириной в определить, во сколько раз увеличатся момент инерции и момент сопротивления относительно центральной оси x, если увеличить вдвое:

1) высоту h или

2) ширину в.

Ответ: увеличатся: 1) J _x в восемь раз, W_x – в четыре;   2) J _x и W_x – вдвое.

 

Задача № 7.

Составить выражения для осевых и центробежных моментов инерции прямоугольника со сторонами в и h относительно центральных осей x и y, повернутых на угол 30⁰к главным осям. Какой вид примут полученные выражения для квадратного сечения со стороной а ?

Ответ: ,  ,  ,  для  квадрата ,   .

 

Задача № 8.

Определить статические моменты плоского прямоугольного сечения относительно осей х и у (рис. 1).

Определить координаты центра тяжести плоского сечения в форме половины круга радиусом R (рис. 2).

Ответ к рис. 1: S_x = bh²/2;    S_y = hb²/2.

 

Задача № 9.

Определить координаты центра тяжести плоского сечения, ограниченного осью х, квадратной параболой x = hy²/b² и прямой линией х = h (рис. 1).

Определить координаты центра тяжести плоского сечения, ограниченного осью х, кубической параболой x = hy³/b³ и прямой линией x = h (рис. 2).

Определить координаты центра тяжести плоского сечения, ограниченного осью у, кубической параболой x = hy³/b³ и прямой линией у = в (рис. 2).

Решение к рис.1. Для нахождения центра тяжести воспользуемся формулами  В первую очередь по формуле  определяем площадь поперечного сечения

Затем по формулам  находим статические моменты сечения:

И, окончательно, по формулам  определяем

Ответ к рис 1: x_1c = 0,375b;  y_1c = 0,6h.

Ответ к рис 2: x_1c = 4h/7;  y_1c = 0,4b.

Ответ к рис.3: x_2c = 2h/7;  y_2c = 0,8b.

 

Задача № 10.

Определить центр тяжести поперечного сечения, показанного на рисунке.

Указания. Для определения положения центра тяжести сложного сечения рекомендуется следующий порядок действий:

1. Сложное сечение разбивается на части, имеющие вид простых фигур.

2. Определяются площади и положения центров тяжести каждой простой фигуры.

3. Выбираются случайные (произвольные) координатные оси х и у. Случайные оси желательно выбирать так, чтобы все точки плоского поперечного сечения имели положительные координаты.

4. По формулам   которые можно записать как

        

вычисляются статические моменты S_x и S_y всего плоского сечения как суммы статических моментов S_xi, S_yi каждой фигуры относительно осей x, y.

5. По формулам  вычисляются координаты центра тяжести всего сечения.

Ответ: х_с = 5а/6; у_с = 5а/6 (Центр тяжести С должен лежать на оси симметрии поперечного сечения).

 

Задача № 11.

Определить статические моменты S_x, S_y сложного поперечного сечения (см. рис.) и найти координаты его центра тяжести.

Указание. Рассматриваемое сложное сечение разбить на три прямоугольника.

Ответ: S_x = 7h³/64,  S_y = 19h³/512;  x_c = 19h/112;  y_c = h/2.

 

Задача № 12.

Определить осевые моменты инерции прямоугольника высотой h  и шириной b относительно осей х и у .

Решение. Имеем dA = bdy. Площадь элементарной площадки подставляем в формулу:

Аналогичным путем можно вычислить I_y = hb³/3.

 

Задача № 13.

Определить осевые моменты инерции прямоугольника высотой h  и шириной b относительно осей х и у, являющихся его осями симметрии (см. рис.).

Ответ: I_x = bh³/12;  I_y = hb³/12.

 

Задача № 14.

Определить осевые моменты инерции I_x, I_y для квадратного поперечного сечения (рис. 1).

Определить осевые моменты инерции I_x, I_y для поперечного сечения, показанного на рис. 2.

  

Ответ к рис.1: I_x = I_y= a⁴/12.

Ответ к рис.2: I_x = (bh³ – b₁h₁³)/12; I_y = (hb³ – h₁b₁³)/12.

 

Задача № 15.

Определить величины главных центральных осевых моментов инерции  составного сечения.

      

 

Задача № 16.

Определить осевые моменты инерции ,и центробежный момент инерции относительно центральных осей х_с, у_с для сечения, изображенного на рисунке. Вычислить значения главных моментов инерции и определить расположение главных осей инерции. Центр тяжести поперечного сечения находится в точке С.

Ответ:   .

 

Задача № 17.

Определить главные моменты инерции относительно главных осей х, у для плоского поперечного сечения, показанного на рисунке. Для вычислений принять h = 12 см,b = 8 см, t = 1 см.

Ответ: I_x = 2313,3 см⁴; I_y = 697,3 см⁴.

 

Задача № 18.

Определить статический момент S_x поперечного сечения в виде равнобокой трапеции (см. рис.). Найти положение центра тяжести С. Вычислить главные моменты инерции относительно главных осей х_с, у. Можно ли применить полученные результаты для вычисления соответствующих геометрических характеристик поперечных сечений в виде равнобедренного треугольника и прямоугольника?

Ответ:  

 

Задача № 19.

Определить статические моменты, осевые моменты инерции, центробежные моменты инерции и положение главных осей неравнополочного уголка 1208010 относительно осей х, у и относительно центральных осей х_с, у_с в четырех вариантах (рис. а, б, в, г). Вычислить положение центра тяжести. Для вычислений принять b = 8 см, h = 12 см, t = 1 см.

Ответ: а) S_x = 75,5 см³; y_c = 3,97 см; S_y = 37,5 см³; x_c = 1,97 см;

                I_x = 578,32 см⁴, I_y = 174,32 см⁴;  I_xy = 51,75 см⁴;  = 1,0928;

                   = 23,8^o.

Лекция 5. Кручение, сдвиг, срез

Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

 

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна  (рад/сек), а передаваемая мощность .

Скручивающий момент равен .

Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле

.            

 

Построение эпюр крутящих моментов

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент М_к в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 5.2).

                                           Рис.5.2

 

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

                              (5.1)

из которой вытекает следующая формула:

                          (5.2)

где  – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение  (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюреМ_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

                                Рис. 5.3

 

Пример 1.

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4, а).

                                                  Рис.5.4

 

Решение.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру (рис.5.4, б).

 

Напряжения в поперечном сечении

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.

Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где М_к=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила , момент который относительно оси вала равен . Крутящий момент М_к, в сечении равен

.                                     (5.3)

                                                  Рис.5.5

 

Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной  (рис.5.6).

Правый торец элемента повернется относительно левого на угол , образующая СВ повернется на угол  и займет положение СВ₁. Угол  - относительный сдвиг. Из треугольника ОВВ₁ найдем:

                                Рис.5.6                                                           Рис.5.7

 

.

 Из треугольника СВВ₁: . Откуда, приравнивая правые части, получим

.

На основании закона Гука при сдвиге:

.                                     (5.4)

Подставим выражение (5.2) в (5.1):

.

Откуда

.                                                  (5.5)

Подставим значение   в выражение (5.4) получим:

.

Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.7). При  получим . Наибольшие напряжения возникают в точках контура сечения при :

.

Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

.

Для сплошного круглого сечения

.

Для кольцевого сечения

,

где .

 

Тогда максимальные касательные напряжения равны

.

 

Условие прочности при кручении вала круглого и кольцевого сечения

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

,                            (5.6)

где  берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

- из второй теории прочности

;                                (5.7)

-  из теории Мора

,                                 (5.8)

где .

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

- по третьей теории прочности

,                                              (5.9)

- по четвертой теории прочности

.                                           (5.10)

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , , , то при повороте граней элемента на 45⁰ в новых площадках обнаруживаются только нормальные напряжения, равные по величине   (рис.5.8).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).

 

           

                        Рис.5.8                                                            Рис.5.9

 

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным  - для хрупких материалов и   - для пластичных материалов.

 

Рациональная форма сечения вала

Анализируя эпюру касательных напряжений (рис.5.7) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

 

Деформации при кручении и условие жесткости вала

Из выражения (5.5) следует, что

,

интегрируя которое по длине вала, получим:

.

Если М_к = const и = const по всей длине вала, то

,

где  - жесткость вала при кручении.

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания

.

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

.         

Эта формула выражает условие жесткости вала при кручении. Обычно принимается  на 1 м длины вала.

 

Расчеты на прочность и жесткость валов круглого и кольцевого сечений

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9), ;

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

                                      

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

                                                           

Для сплошного круглого сечения , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

                                                   

Для кольцевого сечения

Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

 .                               (5.11)

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

 но W_ρ = 0,2d³, поэтому

                                                       (5.12)

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

В этой формуле допускаемый относительный угол закручивания  должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p  будет выглядеть следующим образом:

но I_p = 0,1d ⁴ , поэтому

                                   (5.13)

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметреk = d_вн /d, формулы  (5.12) и (5.13) принимают вид:

                                        (5.14)

                       (5.15)

 

Пример 2.

Подобрать диаметр сплошного вала, передающего мощность N=450 л.с. при частоте вращения n=300 об/мин. Угол закручивания не должен превышать одного градуса на 2 метра длины вала;  =40 МПа, G =8 МПа.

Решение.

Крутящий момент определяем из уравнения

Диаметр вала по условию прочности определяется из уравнения

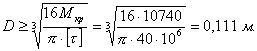
Диаметр вала по условию жесткости определяется из уравнения

Выбираем больший размер 0,112 м.

 

Пример 3.

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающих одинаковый крутящий момент; один из них сплошной, а другой полый с коэффициентом полости . Во сколько раз сплошной вал тяжелее полого?

Решение.

Равнопрочными валами из одинакового материала считаются такие валы, у которых при одинаковых крутящих моментах, возникают одинаковые максимальные касательные напряжения, то есть

.

Условие равной прочности переходит в условие равенства моментов сопротивления:

.

Откуда получаем:

.

Отношение весов двух валов равно отношению площадей их поперечных сечений:

.

Подставляя в это уравнение отношение диаметров из условия равной прочности, получим

.

Как показывает этот результат, полый вал, будучи одинаковым по прочности, вдвое легче сплошного. Это объясняется тем, что в силу линейного закона распределения касательных напряжений по радиусу вала, внутренние слои относительно мало нагружены.

 

Пример 4.

Найти мощность в квт, передаваемую валом, если диаметр сплошного вала , число оборотов вала в минуту , модуль сдвига  и угол закручивания участка вала длиной 7,5 м равен 1/15 ра­диан.

Решение.

Из формулы 

Определим передаваемую мощность

 

Пример 5.

Определить, на сколько процентов увеличится на­ибольшее напряжение вала при кручении, если в валу сделано центральное отверстие  (С=0,4).

Решение.

Полагая , полу­чим следующие выражения для напряжений сплошного и полого валов:

             

Искомая разница в напряжениях

 

Пример 6.

Заменить сплошной вал диаметра = 300 мм по­лым равнопрочным валом с наружным диаметром  =350 мм. Найти внутренний диаметр полого вала  и сравнить веса этих валов.

Решение.

Наибольшие касательные напряжения в обоих валах должны быть равными между собой:                

Отсюда определим коэффициент  С        

Внутренний диаметр полого вала                      

 

Отношение весов равно отношению площадей поперечных сечений:

Из приведенных примеров 5 и 6 видно, что изготовление пусто­телых валов, т.е. валов, у которых малонагруженная внутренняя часть удаляется, является весьма эффективным средством сниже­ния затраты материала, а следовательно, и облегчения веса валов. При этом наибольшие напряжения, возникающие в пустотелом валу, мало отличаются от максимальных напряжений в валу сплошного сечения при том же наружном диаметре.

Так в примере 5 за счет сверления при , да­ющем облегчение вала на 16%, максимальные напряжения в наруж­ных волокнах полого вала возросли всего на 2,6%. В примере 6 равнопрочный пустотелый вал, но с несколько большим наружным диаметром по сравнению со сплошным валом, оказался легче сплошного на 53,4%. Эти примеры наглядно свидетельствуют о рацио­нальности применения пустотелых валов, что широко используется в некоторых областях современного машиностроения, в частности, в моторостроении.

 

Пример 7.

К стальному валу (см.рис.5.10) приложены скручивающие моменты: М₁, M₂, M₃, M₄. Требуется:

1) построить эпюру крутящих моментов;

2) при  заданном значении  определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;

3) построить эпюру углов закручивания;

4) найти наибольший относительный угол закручивания.

Дано: М₁ = М₃ = 2 кНм,  М₂ = М₄ = 1,6 кНм,  а = b = с = 1,2 м,    = 80 МПа.

                                            Рис.5.10

 

Решение.

1. Построить эпюру крутящих моментов.

При построений эпюр М_кр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.

Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты всех поперечных сечений удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Для построения эпюры крутящих моментов необходимо найти величины крутящих моментов на каждом участке вала.

I участок (КД):

 кНм,

II участок (СД):

 кНм,

III участок (СВ):

 кНм,

IV участок (ВА):

 кНм.

По значению этих моментов строим эпюру М_кр в выбранном масштабе. Положительные значения М_кр откладываем вверх, отрицательные - вниз от нулевой линии эпюры (см. рис.5.11).

                                     Рис.5.11

 

2. При заданном значении  определим диаметр вала из расчета на прочность.

Условие прочности при кручении имеет вид

.

- максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры М_кр (рис.5.11).

 кНм;

 - полярный момент сопротивления для сплошного круглого вала.

Диаметр вала определяется по формуле

. 

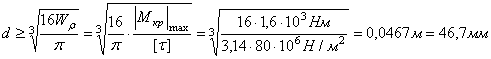Принимаем d = 50 мм = 0,05 м.

3. Построим эпюру углов закручивания.

Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле

.

где  - жесткость сечения вала при кручении.

Н/м²;

 - полярный момент инерции круглого вала

м⁴.

Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А)

 рад,

 рад,

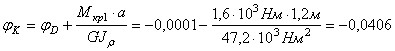рад,

рад.

Строим эпюру углов закручивания (рис.5.11).

4. Найдем наибольший относительный угол закручивания

рад/м.

 

Пример 8.

Определить напряжения и погонный угол закручивания стальной разрезной трубы (рис.5.12), имеющей диаметр средней линии d=97,5 мм и толщину  мм. Крутящий момент – 40 Нм. Модуль сдвига материала трубы G = 8·10⁴ МПа. Сравнить полученные напряжения и угол закручивания с напряжением и углом закручивания для сплошной трубы.

                                     Рис.5.12

 

Решение.

Касательные напряжения в разрезной трубе, представляющей собой тонкостенный стержень, определим по формуле

где - развернутая длина осевой линии трубы.

Напряжение в сплошной трубе определяется по формуле

Угол закручивания на метр длины для разрезной трубы определяется по формуле

Погонный угол закручивания для сплошной трубы определяется по формуле

Таким образом, в сплошной трубе по сравнению с разрезанной вдоль образующей при кручении напряжения меньше в 58,3 раза, а угол закручивания – в 1136 раз.

 

 

Потенциальная энергия деформации при кручении.

Элементарная работа статически приложенного внешнего момента Т на перемещении   равна:

.

При чистом кручении М_к = Т и .

Потенциальная энергия деформации

;

интегрируя выражение для элементарной работы по всей длине l стержня, получим

.

При М_к = const и = const, получим

.

 

Статически неопределимые задачи на кручение

Как известно, статически неопределимыми называют задачи, в которых число неизвестных опорных реакций или число внутренних усилий превышает число возможных уравнений статики. Один из методов решения статически неопределимых задач сводится к следующему:

а) составляются все возможные в данной задаче уравнения статики;

б) представляется картина деформации, происходящей в данной конструкции, и записываются деформационные уравнения, число которых должно быть равно степени статической неопределимости задачи;

в) решается совместная система уравнений статики и деформационных уравнений.

 

 

Кручение бруса с некруглым поперечным сечением

Определение напряжений в брусе с некруглым поперечным се­чением представляет собой сложную задачу, которая не может быть решена методами сопротивления материалов. Причина заключается в том, что для некруглого поперечного сечения упрощающая гипо­теза плоских сечений, оказывается неприемлемой. В данном случае поперечные сечения существенно искривляются, в результате чего заметно меняется картина распределения напряжений.

Таким образом, при определении углов сдвига, в данном слу­чае, необходимо учитывать не только взаимный поворот сечений, но и деформации сечений в своей плоскости, связанная с искрив­лением сечений.

Задача резко усложняется тем, что для некруглого сечения, на­пряжения должны определяться как функции уже не одного неза­висимого переменного , а двух  x и y.         

Отметим некоторые особенности законов распределения напря­жений в поперечных сече­ниях некруглой формы. Ес­ли поперечное сечение име­ет внешние углы, то в них касательные напряжения должны обращаться в нуль. Если наружная поверхность бруса при кручении свобод­на, то касательные напряже­ния в поперечном сечении, направленные по нормали к контуру также будут равны нулю.

На рис. 4.3 показана, по­лученная методом теории упругости, эпюра касатель­ных напряжений для бруса прямоугольного сечения. В углах, как видно, напряже­ния равны нулю, а наиболь­шие их значения возникают по серединам больших сторон:

в точке А 

,                                                             (5.16)

где   момент сопротивления при кручении, аналог полярного момента сопротивления попереч­ного сечения прямоугольного бруса;

                                   Рис. 5.13

 

в точке В              

,                                                                                  (5.17)

здесь необходимо учесть, что b  малая сторона прямоугольника.

Значения угла закручивания определяется по формуле:

,                                                                               (5.18)

где   момент инерции при кручении, аналог полярного момента инерции поперечного сечения бруса.

Коэффициенты ,  и  зависят от отношения сторон , и их значения приведены в табл. 4.1.

                                                                                            

Таблица 4.1. Значения коэффициентов для прямоугольных сечений

1,0	0,208	0,140	1,0
1,2	0,219	0,166	-
1,4	0,228	0,187	0,865
1,6	0,234	0,204	0,845
1,8	0,240	0,217	-
2,0	0,246	0,229	0,796
2,5	0,258	0,249	-
3,0	0,267	0,263	0,753
4,0	0,282	0,281	0,745
6,0	0,299	0,299	0,743
8,0	0,307	0,307	0,743
10,0	0,313	0,313	0,743
Более 10	0,333	0,333	0,743

               

Значения ,  и  для различных сечений приведены в табл.4.2.

                                                                                                                                                     

Таблица 4.2. Геометрические характеристики жесткости и прочности для

некоторых сечений при кручении прямого бруса

Форма поперечного сечения	Момент инерции при кручении	Момент сопротивления при кручении	Наибольшие касательные напряжения
Квадрат			В серединах сторон В углах
Круг с лыской			В середине плоского среза
Эллипс			В конце малой полуоси большой
Равносторонний треугольник			В серединах сторон в углах
Правильный шести- или восьмиугольник	(для шестиугольника , для восьмиугольника)	(для шестиугольника , для восьмиугольника)	В серединах сторон в углах
Форма клина			В точках длинных сторон ближе к широкому основанию
Полое эллиптическое сечение	; (); ()		В конце малой полуоси , большой , при малой толщине  (равномерно по сечению)
Незамкнутое кольцевое сечение			В точках внутреннего и наружного сечения

 

Пример 9.

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающие одинаковый крутящий момент; один из них круглого поперечного сечения, а другой - квадратного. Во сколько раз квадратный вал тяжелее круглого?

Решение.

Условие равной прочности имеет следующий вид:

,

где ; значение коэффициента  определяется по таблице 4.1 и составляет для квадратного сечения ()  .

Из условия равной прочности получаем:

.

Отношение весов двух валов равно отношению площадей их поперечных сечений:

.

Подставляя в это уравнение отношение  из условия равной прочности, получим

.

 

Сдвиг

Сдвигом называют деформацию, представляющую собой искажение первоначально прямого угла малого элемента бруса (рис.5.14) под действием касательных напряжений . Развитие этой деформации приводит к разрушению, называемому срезом или, применительно к древесине, скалыванием. Примером сдвига является резка полосы ножницами. На сдвиг работают жесткие соединения конструкций – сварные, заклепочные и так далее.

 

Деформация сдвига оценивается взаимным смещением  граней 1 – 1 и 2 – 2 малого элемента (рис. 5.15), называемым абсолютным сдвигом и более полно –относительным сдвигом (углом сдвига) 

,                                      (5.19)

являющимся безразмерной величиной.

      

В предположении равномерного распределения касательных напряжений по сечению площадью А, они определяются по формуле

,                                                 (5.20)

где Q – поперечная сила в данном сечении.

Условие прочности записывается по минимальной площади среза S_min, отражающей минимальное число соединяющих элементов (заклепок, болтов, штифтов и т.д.) или минимальную длину сварного шва.

Величина допускаемых напряжений  зависит от свойств материала, характера нагрузки и может быть определена по 3-ей теории прочности: , а так как при чистом сдвиге  , то

,                     (5.21)

При расчете болтовых или заклепочных соединений учитывается смятие контактирующих поверхностей, то есть пластическую деформацию, возникающую на поверхности контакта.

,

где A_см – площадь проекции поверхности контакта на диаметральную плоскость.

При выполнении проектного расчета, то есть при определении необходимого диаметра заклепки, болта или при определении их количества необходимо учитывать условие прочности на срез и на смятие, из двух значений следует взять большее число, округлив его до ближайшего целого в меньшую сторону.

Примечания: 1. Так как болты и заклепки ослабляют соединяемые листы, последние проверяют на разрыв в ослабленных сечениях

.

При расчетах сварных швов наплывы не учитывают, а считают, что в разрезе угловой шов имеет форму прямоугольного равнобедренного треугольника и разрушение шва происходит по его минимальному сечению, высота которого

,

где – минимальная толщина соединяемых листов.

В пределах упругости касательное напряжение прямо пропорционально относительному сдвигу

                                               (5.22)

– это закон Гука при сдвиге; G – модуль сдвига, Н/м², характеризующий жесткость материала при сдвиге.

Закон Гука при сдвиге через абсолютные деформации:

,                                    (5.23)

где а – расстояние между сдвигаемыми гранями; А – площадь грани.

Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона  материала связаны зависимостью

Удельная потенциальная энергия деформации сдвига равна

На практике чаще всего теория сдвига применяется к расчету болтов, заклепок, шпонок, сварных швов и других элементов соединений.

 

Расчет заклепок на срез

Мы изучали, что при простом растяжении или простом сжатии две части стержня, разделенные наклонным сечением, стремятся не только оторваться друг от друга, но и сдвинуться одна относительно другой. Растяжению сопротивляются нормальные, а сдвигу — касательные напряжения.

На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига.

В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).

   Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (рис.5.16). Шесть заклепок, расположенных в два ряда, соединяют два листавнахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил P).

 

                                                     Рис.5.16.

 

Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов.

На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при заклепках в соединении, изображенном на рис.5.16, на каждую из них действуют по две равные и противоположные силы  (рис.5.17); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы  стремятся перерезать заклепку по плоскости mk раздела обоих листов.

                          Рис.5.17.

 

Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (рис.5.17). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу  т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную . Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательныенапряжения . Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение:

Величина допускаемого касательного напряжения , или, как говорят, допускаемого напряжения на срез, принято определять в виде: .  Зная , мы напишем условие прочности заклепки на перерезывание в таком виде:

т. е. действительное касательное напряжение  в материале заклепки должно быть равно допускаемому , или меньше его.

Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно ) и определяют необходимое число заклепок :

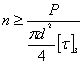
Знаменатель этой формулы представляет собой ту силу, которую безопасно может взять на себя каждая заклепка.

Пусть ; тогда

                                                  Рис.5.18

 

При выводе формулы расчета заклепки на перерезывание, помимо оговоренных, допущена еще одна неточность. Дело в том, что силы  действующие на заклепку, не направлены по одной прямой, а образуют пару. Эта пара уравновешивается другой парой, образующейся из реакций соединенных листов на головку заклепки (рис.5.18) и ведет к появлению нормальных напряжений, действующих по сечению mk.

Кроме этих нормальных напряжений, по сечению mk действуют еще нормальные напряжения, вызванные тем, что при охлаждении заклепочный стержень стремится сократить свою длину, чему мешает упор головок заклепки в листы. Это обстоятельство, с одной стороны, обеспечивает стягивание заклепками листов и возникновение между ними сил трения, с другой — вызывает значительные нормальные напряжения по сечениям стержня заклепки. Особых неприятностей эти напряжения принести не могут. На заклепки идет сталь, обладающая значительной пластичностью; поэтому даже если бы нормальные напряжения достигли предела текучести, можно ожидать некоторого пластического удлинения стержня заклепки, что вызовет лишь уменьшение сил трения между листами и осуществление в действительности той схемы работы заклепки на перерезывание, на которую она и рассчитывается. Поэтому эти нормальные напряжения расчетом не учитываются.

При проектировании строительных конструкций применяется следующее условие прочности на срез для заклепок и болтовых соединений

                                           (5.24)

где Q – поперечная сила, равная внешней силе F, действующей на соединение; R_bs – расчетное сопротивление на срез;  – расчетная площадь сечения болта или заклепки; d – диаметр заклепки или наружный диаметр болта; n_s – число срезов одного болта или заклепки;  – коэффициент условий работы соединения, имеющий значения в интервале ; n – число болтов или заклепок.

Если величины F, R_bs, , n_s известны, то задаваясь числом заклепок или болтов n, можно найти необходимый для обеспечения прочности на срез диаметр

.                                             (5.25)

А зная d, F, R_bs, , n_s, можно определить потребное число заклепок или болтов

                                              (5.26)

 

 

Расчет заклепок на смятие и листов на разрыв

Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.

Так как передача сил на заклепочный стержень происходит путем нажатия стенок заклепочного отверстия на заклепку, то необходимо установить, не произойдет ли наружное обмятие этого стержня или стенок отверстия, — произвести проверку на смятие.

Под смятием понимают пластическую деформацию, возникающую в соединениях на поверхностях контакта. Возникающие при этом напряжения являются нормальными, закон распределения которых по поверхности контакта достаточно сложен.

На рис.5.20 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению  в точке А поверхности заклепки.

                                                           Рис.5.20

 

Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки.

Так как давление на одну заклепку равно , то

условие прочности на смятие будет иметь вид:

где  — допускаемое напряжение на смятие. Отсюда необходимое число заклепок

Допускаемое напряжение на смятие принимают обычно в 2 - 2,5 раза больше основного допускаемого напряжения на растяжение и сжатие , так как расчет на смятие по существу является упрощенной проверкой прочности по контактным напряжениям.

Таким образом, определяется число заклепок, необходимое для прочного соединения листов. Из двух полученных значений , конечно, надо взять большее.

Если мы вернемся к рассмотренному ранее примеру и примем , ,то получим:

Таким образом, условие прочности заклепок на перерезывание требует постановки двадцати четырех заклепок; условие же прочности на смятие — пятнадцати заклепок. Очевидно, необходимо поставить двадцать четыре заклепки. В этом примере работа заклепок на срез оказывается опаснее работы их на смятие. Это обычно бывает в соединениях с так называемыми односрезными заклепками, в которых каждая заклепка перерезывается в одной плоскости.

                                  а) расчетная схема,                         б) действующие усилия

                                                        Рис.5.21

 

В несколько других условиях будут работать заклепки соединения, показанного на рис.5.21,а. Здесь стык двух листов осуществлен при помощи двух накладок. Сила Рпри помощи первой группы заклепок передается от левого листа обеим накладкам, а от последних при помощи второй группы заклепок передается правому листу.

Называя через  число заклепок, необходимое для передачи усилия Р от листа на накладки и от накладок на другой лист, получаем, что на каждую заклепку передается усилие от основного листа . Оно уравновешивается усилиями , передающимися на заклепку от накладок (рис.5.21, б).

Стержень заклепки теперь подвергается перерезыванию уже в двух плоскостях; средняя часть заклепки сдвигается влево. Допускают, что срезывающая сила  равномерно распределяется по двум сечениям, mk и gf. Напряжение  и условие прочности для двухсрезной заклепки принимает вид:

и 

Таким образом, при двойном перерезывании число заклепок по срезыванию оказывается в два раза меньше, чем при одиночном перерезывании.

Переходим к проверке на смятие. Толщина склепываемых листов ; толщина накладок  не должна быть меньше 0,5t, так как две накладки должны взять от основного листа всю силу Р. Поэтому:

Сила сминает и среднюю часть заклепки и верхнюю с нижней. Опаснее будет смятие той части, где площадь смятия меньше.

Так как толщина среднего листа не больше суммы толщин обеих накладок, то в худших условиях по смятию будет средняя часть заклепки. Условие прочности на смятие останется таким же, как и при односрезных заклепках:

Таким образом, для рассматриваемой конструкции число заклепок в первой и во второй группах определится из полученных условий.

Пусть 

Тогда:

.

В этом случае при двухсрезных заклепках условия их работы на смятие тяжелее, чем на срезывание; следует принять .

На двух рассмотренных примерах мы установили общие методы проверки прочности заклепочных соединений. В металлических конструкциях иногда приходится склепывать целые пакеты соединяемых элементов. В таких пакетах заклепки могут работать и на большее число срезов. Однако методы расчета многосрезных заклепок не отличаются от изложенных. Для вычисления касательных напряжений следует разделить силу, относящуюся к одной заклепке, на суммарную площадь среза, воспринимающую эту силу. Для вычисления же напряжений смятия следует найти ту часть заклепки, которая находится в наиболее опасных условиях, т. е. воспринимает наибольшую силу на наименьшем протяжении. Напряжения смятия получаются делением этой силы на площадь диаметрального сечения наиболее напряженной части заклепки. Затем останется написать два условия прочности и получить .

Наличие заклепок вносит некоторые изменения и в проверку прочности на растяжение или сжатие самих склепанных листов. Опасным сечением каждого листа (рис.5.22) будет теперь сечение, проходящее через заклепочные отверстия; здесь рабочая ширина листа будет наименьшей; принято говорить, что это сечение ослаблено заклепочным отверстием. Называя полную ширину листа b, получаем для него такое условие прочности:

где — число отверстий, попадающих в сечение (в нашем случае — два).

 

                                                                Рис.5.22

 

Отсюда можно найти величину , задавшись толщиной листа t. Площадь  ослабленного сечения называется площадью нетто, площадь же полного сечения листа называется площадью брутто.

Этот учет влияния заклепочных отверстий на прочность склепываемых листов общепринят, но является весьма условным. На самом деле, влияние отверстия в листе вызывает у его краев, на концах диаметра, перпендикулярного к направлению растяжения, значительные местные напряжения, которые могут достичь предела текучести материала и вызвать остаточные деформации, захватывающие, однако, весьма небольшой объем материала листа.

Некоторую опасность в отношении образования трещин эти местные напряжения могут представить лишь при действии переменных нагрузок в материале, имеющем низкий предел усталости. Однако в обычных условиях работы заклепочных соединений эта опасность может считаться исключенной. Во избежание возможности разрушения листов заклепками заклепки размещаются на определенных расстояниях друг от друга и от края листа.

Расположение заклепок в плане производится как по условиям обеспечения прочности и плотности соединения, так и по чисто производственным соображениям. Расстояния между центрами заклепок принимаются не менее 3d и не более 7d. Расстояния до края листов должны быть не менее (рис.5.23). Чтобы длина стыка былавозможно меньше, берут , а в целях меньшего ослабления сечения расстояние е берут возможно большим (до 7d), что позволяет уменьшить число рядов, а следовательно, и ослабление.

              Рис.5.23. Практические рекомендации по расположению заклепок в соединении.

 

При проектировании заклепочных соединений для котлов и резервуаров, где добиваются плотных швов, помимо расчета на срез производят проверку сопротивления скольжению за счет трения. Однако допускаемое напряжение по скольжению дается в МПа поперечного сечения заклепки; таким образом, проверка на трение при односрезных заклепках сводится к проверке на срез лишь с другим допускаемым напряжением. При двухсрезных заклепках в расчет на трение вводится, конечно, одна площадь сечения заклепки, но зато повышается почти вдвое допускаемое напряжение на трение за счет двух накладок.

Поэтому так называемый расчет заклепок на трение является, по существу, проверкой прочности на срез с другими лишь допускаемыми напряжениями на квадратный сантиметр площади поперечного сечения заклепки.

Правильнее было бы сохранить лишь один метод проверки заклепочных соединений на смятие и срез, учитывая влияние сил трения при назначении допускаемых напряжений в зависимости от способа клепки, качества отверстий и требований, предъявляемых ко шву в отношении плотности.

В заклепочных соединениях для котлов принимают обычно допускаемое напряжение на скольжение (на 1 см² площади заклепки):

- от 50 до 70 МПа при швах внахлестку,

- от 90 до 120 с двумя накладками.

При проверке по этим данным, очевидно, надо вести расчет, как при заклепках одиночного перерезывания, с допускаемым напряжением от 50 до 70 или от 90 до 120МПа.

При проектировании строительных конструкций применяется следующий алгоритм расчета болтовых и заклепочных соединений на смятие.

 

Упрощая расчет, площадь, подвергающуюся смятию, принимают равной

где d – диаметр заклепки (болта); n – их число;  – наименьшая суммарная толщина элементов, сминаемых в одном направлении. Сминающей будет та же сила F, которая производит и срез. Таким образом, условие прочности на смятие имеет вид:

                                     (5.27)

где R_bp – расчетное сопротивление на смятие.

Из условия (5.27) можно найти либо необходимый диаметр d по известным величинам F, t, n, R_bp,:

,                                               (5.28)

либо определить потребное число заклепок n

.                                               (5.29)

Из двух значений диаметров, рассчитанных по формулам (5.25) и (5.28), берут больший, округляя его до стандартного значения. Точно так же из двух значений n, рассчитанных по формулам (5.26) и (5.29), выбирают большее число, естественно, округленное до большего целого.

У к а з а н и я

1. В заклепочных и болтовых соединениях при действии поперечной силы Q , проходящей через центр тяжести соединения, распределение этой силы между заклепками или болтами принимают равномерным.

2. При действии на соединение момента, вызывающего сдвиг соединяемых элементов, распределение усилий на болты или заклепки следует принимать пропорционально расстояниям от центра тяжести соединения до рассматриваемого болта или заклепки.

3. Болты или заклепки, работающие одновременно на срез и растяжение, следует проверять отдельно на срез и на растяжение.

 

Дополнительные задачи на сдвиг

Задачи на сдвиг встречаются не только при расчете заклепочных и болтовых соединений. Имеются и другие элементы конструкций, испытывающие деформацию сдвига, и поэтому при их расчете необходимо всякий раз удовлетворять условию прочности на срез

                                       (5.30)

и условию прочности на смятие

                                   (5.31)

Например, при расчете соединения деревянных элементов в качестве условия (5.30) применяется условие прочности на скалывание вдоль волокон

                                       (5.32)

где  R_ск – расчетное сопротивление скалыванию.

Условие прочности на смятие в деревянных конструкциях вдоль волокон имеет вид соотношения (5.31).

 

Пример 10.

Определить из условия прочности размеры стержня (рис.5.25) при допускаемых напряжениях при растяжении = 160 МПа, срезе = 80 МПа и смятии  = 170 МПа.

                 Рис.5.25

 

Решение.

Диаметр  стержня определим из условия прочности при растяжении

 или ,

откуда

.

Принимаем =20 мм.

Высоту головки стержня определяем из условия ее прочности при срезе

,

где .

Если прочность головки стержня окажется недостаточной, она срежется по поверхности цилиндра диаметром и высотой . Образующие поверхности среза Ппоказаны на рисунке 5.25 волнистыми линиями. Подставив в условие прочности выражение для площади среза, получим

,

откуда

Принимаем =10 мм.

Действующую силу  воспринимает опорная кольцевая поверхность головки стержня. Диаметр  головки стержня определяем из условия прочности опорной поверхности головки при смятии

 или ,

откуда

Принимаем =28 мм.

 

Пример 11.

Обосновать соотношение между диаметром d и высотой головки h болта (рис. 5.26), если .

                      Рис. 5.26

 

Решение.

Срез головки болта происходит по цилиндрической поверхности .

Условие прочности на срез имеет вид:

.

Условие прочности на растяжение стержня болта имеет вид:

.

Предельное отношение касательных и нормальных напряжений определяет искомое соотношение между высотой головки болта и его диаметром:

;     .

 

Расчет сварных соединений

При изготовлении металлических конструкций часто применяется сварка с помощью электрической дуги.

Впервые электрическая дуга была открыта русским ученым проф. В. В. Петровым в 1802 г. Обнаружив плавление металла в пламени полученной им электрической дуги, проф. Петров указал на возможность использования этого явления в технике. Однако электрическая дуговая сварка была изобретена лишь в конце XIX века русскими инженерами Н. Н. Бенардосом (1882 г.) нашим земляком и Н. Г. Славяновым (1888 г.) и получила впоследствии широкое распространение во всем мире.

Сущность электросварки по методу Славянова заключается в том, что, расплавляя электрической дугой материал электрода (сталь), заполняют им стык соединяемых элементов, также прогреваемых дугой до температуры плавления. В результате, после остывания расплавленного металла, образуется шов, прочно соединяющий стыкуемые элементы. Схема сварки показана на рис.5.27. Электрическая дуга горит между металлическим электродом и свариваемым металлом, расплавляя электрод и кромки соединяемых элементов металла, между которыми образуется так называемая сварочная ванна.

                  Рис.5.27. Технологическая схема сварки

 

Для защиты плавящегося металла от попадания вредных включений из окружающего воздуха на поверхность электрода наносится толстая защитная обмазка, выделяющая при плавлении электрода большое количество шлака и газов, благодаря чему плавящийся металл изолируется от окружающего воздуха.

Этим обеспечивается высокое качество металла сварного шва, механические свойства которого могут резко ухудшиться под влиянием кислорода и азота воздуха (при отсутствии обмазки или при тонкой обмазке). С той же целью автоматическая сварка производится под слоем флюса, защищающим плавящийся металл от попадания кислорода и азота воздуха.

При правильном выборе конструкции соединений, материалов и технологии сварки сварные соединения по надежности не уступают заклепочным при действии как статических, так и динамических нагрузок (в том числе ударных и знакопеременных). В то же время электросварка имеет ряд преимуществ перед клепкой, из которых важнейшими являются меньшая трудоемкость сварочных работ и отсутствие ослабления сечений соединяемых элементов отверстиями. Это дает значительную экономию средств и металла, помимо экономии, получаемой за счет большей компактности соединений. Большие экономические выгоды, приносимые электросваркой, и даваемое ею упрощение конструкций привели в последнее время к постепенному вытеснению заклепочных соединений сварными.

Значительное развитие электросварка получила в СССР благодаря трудам советских ученых Патона, Вологдина, Никитина, Хренова и др., разработавших новые методы сварки, обеспечивающие высокую прочность соединений.

Методы расчета сварных соединений тесно связаны с технологией сварки, причем для многих видов соединений расчет носит весьма условный характер. Вообще методику расчета сварных соединений нельзя еще считать установившейся.

Что касается норм допускаемых напряжений для материала швов, то они принимаются различными в зависимости от способа сварки (ручная и автоматическая), а также от состава и толщины защитной обмазки электродов.

В таблице 4.3. приведены допускаемые напряжения для сварных швов в конструкциях из стали марки ст. 3 по существующим нормам.

 

Таблица 4.3. Допускаемые напряжения при сварке.

Вид напряжения	Обозначение	Ручная сварка		Автоматическая сварка
		Электроды с тонкой обмазкой	Электроды с толстой обмазкой
Растяжение   Сжатие   Срез		1000 кг/см2   1100 кг/см2   800 кг/см2	1800 кг/см2   1450 кг/см2   1100 кг/см2	1300 кг/см2   1450 кг/см2   1100 кг/см2

 

При проверке прочности сварных швов учитывается возможный непровар в начале шва и образование кратера в конце. Поэтому расчетная длина шва принимается меньшей, чем действительная или проектная на 10 мм.

Существует несколько типов сварных соединений. При соединении встык зазор между соединяемыми элементами заполняется наплавленным металлом. Типы сечений стыковых швов в зависимости от толщины соединяемых элементов показаны на рис. 5.28. В зависимости от направления действующего усилия F по отношению к шву их подразделяют на прямые и косые (рис. 5.29).

      

Необходимо отметить, что наиболее простым и надежным видом соединения является соединение встык, образуемое путем заполнения зазора между торцами соединяемых элементов наплавленным металлом. Соединение встык осуществляется, в зависимости от толщины соединяемых элементов, по одному из типов, показанных на рис.5.30. Проверка прочности производится на растяжение или сжатие по формуле:

                  Рис.5.30. Расчетная схема сварного соединения.

 

Здесь — условная рабочая площадь сечения шва, где расчетная длина шва , а высота шва h принимается равной толщине свариваемых элементов t.

Поскольку допускаемое напряжение для сварного шва ниже, чем для основного металла, стремятся к увеличению длины стыкового шва. С этой целью применяют соединение встык с косым швом (рис.5.31). Исследования таких соединений, произведенные Институтом электросварки Академии наук УССР, показали, что равнопрочность их с основным металлом всегда обеспечивается.

Проверка прочности косых швов производится и по нормальным и по касательным напряжениям, возникающим по сечению шва mn:

        Рис.5.31. Расчетная схема косого сварного соединения.

 

Имея в виду, что  получим:

                                                                       

Здесь расчетная длина шва по техническим условиям принимается равной .

Как установлено опытом, наиболее рациональным углом наклона шва к линии действия сил является. Недостатком соединения косым швом является неудобство центрировки стыкуемых элементов при сварке, поэтому его применяют редко.

Иногда соединение листов производится внахлестку или встык с перекрытием накладками. Это вызывает необходимость сваривать листы, не лежащие в одной плоскости, что осуществляется при помощи так называемых валиковых (или угловых) швов — лобовых или торцевых (перпендикулярных к направлению действующей силы) и боковых или фланговых (параллельных ей).

Валиковый шов в сечении имеет довольно неопределенную форму (рис.5.32). В теоретических расчетах на прочность сечение шва принимается в виде равнобедренного треугольника (очерченного пунктиром) с расчетной высотой ).

                           а) технология.            б) расчетная схема

       Рис.5.32. Сварное соединение внахлестку:

 

Соединения торцевыми (лобовыми) швами показаны на рис.5.33. Разрушение таких швов происходит по наиболее слабому сечению AB, как это установлено опытами.

              Рис.5.33. Сварное соединение торцевыми швами

 

Как это видно из рис.5.32, б, полное напряжение, возникающее в сечении АВ, может быть разложено на нормальную и касательную составляющие. Поскольку сопротивление стали сдвигу ниже, чем при растяжении, расчет лобовых швов производится условно на срез в предположении равномерного распределения касательных напряжений по площади сечения АВ. Имея в виду, что на восприятие силы Р в этих соединениях (рис.5.33) работают два лобовых шва, верхний и нижний, получим:

Так как площадь сечения шва, а расчетная длина , то условие прочности примет вид:

В действительности, материал шва испытывает сложное напряженное состояние, причем напряжения по сечению АВ распределяются неравномерно. Исследования, произведенные методами теории упругости и подтвержденные экспериментально, показали, что в углах шва имеет место высокая концентрация напряжений.

Если учесть, что, вследствие укорочения швов при остывании, в зоне сварки возникают дополнительные напряжения и в основном металле, ведущие к переходу его в хрупкое состояние, то следует иметь в виду, что концентрация напряжений может явиться причиной появления трещин в основном металле соединения.

Поэтому такое соединение не может быть рекомендовано, особенно при переменной или ударной нагрузке. Значительно надежнее работа соединения встык без накладок.

Соединение фланговыми (или боковыми) швами показано на рис.5.34, а. Разрушение шва, показанное на рис.5.34, б, происходит на значительном его протяжении путем срезывания наплавленного металла в направлении, параллельном шву по наиболее слабой плоскости АВ.

               Рис.5.34. Соединение фланговыми швами а) и его разрушение б)

 

Условие прочности для двух симметрично расположенных швов имеет вид:

Если стык перекрыт двухсторонними накладками, число швов удвоится и условие прочности примет вид:

Отсюда обычно определяют необходимую расчетную длину  фланговых швов. Проектная же длина каждого шва принимается равной .

Как показали опыты, разрушение фланговых швов происходит по типу разрушений пластичных материалов со значительными остаточными деформациями. Это делает работу фланговых швов более благоприятной, чем работу лобовых швов. Однако следует иметь в виду, что у концов фланговых швов также имеет место высокая концентрация напряжений.

При проектировании часто стремятся обеспечить большую надежность соединения, применяя вместо сварки встык, или в дополнение к ней, перекрытие стыка накладками, которые привариваются фланговыми или торцевыми швами, а иногда и теми и другими вместе. Как уже указывалось, при переменных и ударных нагрузках такое «усиление» стыка может принести больше вреда, чем пользы.

Что касается расчета такого комбинированного стыка, то при одновременном применении лобовых и фланговых швов считают, что сопротивление соединения равно сумме сопротивлений всех швов, т. е., где сопротивление торцевого шва при расчетной длине  равно, а сопротивление двух фланговых швов, причем , где b — ширина накладки. В результате подстановки получаем:

.

Зная длину торцевого шва, определяют длину фланговых швов .При двухсторонних накладках число швов удваивается, т. е. правую часть полученного соотношения следует удвоить.

Так как торцевые швы более жестки, то при совместной работе с фланговыми они перегружаются, что ведет к неравномерной работе соединения. Если учесть, что в таком соединении и термические напряжения достигают больших значений, то устройства такого стыка следует избегать.

Иногда при соединении внахлестку, в дополнение к фланговым швам, применяют прорезные швы, осуществляемые путем наплавки металла в узкую прорезь, сделанную в одном из соединяемых элементов параллельно действующему на соединение усилию.

                Рис.5.35. Комбинация фланговых и прорезных швов

 

При длине прорезного шва  и ширине прорези d сопротивление такого шва срезу равно:

где — усилие, приходящееся на прорезной шов.

В комбинированном соединении с фланговыми швами для записи расчетного условия принимают, что или

Задавшись размерами одного из швов (обычно флангового), находят необходимую длину другого. При этом ширина прорези d принимается равной двойной толщине прорезанного металла, длина — не более двадцати толщин.

Недостатками соединения с прорезными швами являются: 1) ослабление сечения прорезями вследствие неизбежного непровара и 2) высокая концентрация напряжений в основном металле в зоне сварки, ведущая к появлению трещин около углов прорезного шва; поэтому такое соединение может применяться лишь в крайних случаях, при условии хорошо продуманной технологии сварочных работ.

В заключение заметим, что в том случае, когда приходится прибегать к соединению внахлестку, лучше всего ограничиться одними фланговыми швами, избегая комбинированных соединений.

 

Расчет сварных соединений при проектировании строительных конструкций

Прочность сварных швов характеризуется их расчетным сопротивлением. В основе расчета прямых стыковых швов лежит условие прочности на растяжение или сжатие:

              (5.33)

где – расчетная длина сварного шва; t – наименьшая толщина соединяемых элементов; – расчетное сопротивление сварного соединения на растяжение или сжатие по пределу текучести  (иногда берут  – то же – по пределу прочности);  – коэффициент условий работы ().

Необходимо иметь в виду, что вследствие дефектов сварного шва на его концах, окончательную длину назначают, прибавляя к рассчитанной по формуле (5.33) длине по 1 см на каждом конце.

В основе расчета косых стыковых швов лежат:

–  условие прочности на растяжение (сжатие) в направлении, перпендикулярном шву:

;        (5.34)

– условие прочности на срез в направлении вдоль шва:

,         (5.35)

где – расчетное сопротивление сварного соединения на срез.

Соединение внахлестку выполняется при помощи угловых швов, которые могут быть лобовыми (рис. 5.36, а) и фланговыми (рис. 5.36, б).

При соединении внахлестку расчет угловых швов производится  на срез (условный) по двум сечениям (рис. 5.37): по металлу шва (сечение 1) и по металлу границы сплавления (сечение 2). При рассмотрении сечения 1 условие прочности записывается в виде

                                (5.36)

а для сечения 2 в виде

                                  (5.37)

В этих формулах:  – расчетная длина шва, принимаемая меньше его полной длины на 1 см;  и  – коэффициенты, зависящие от прочности материала свариваемых элементов, вида сварки и принимаемые от 0,7 до 1,15;  и – коэффициенты условий работы шва, принимающие значения от 0,85 до 1,0 в зависимости от районов эксплуатации конструкции;  и  – расчетные сопротивления сварных соединений при срезе соответственно по металлу шва и металлу границы сплавления;  – коэффициент условий работы шва и назначения конструкции (); k_f – длина катета сварного шва.

Из двух длин , рассчитанных по формулам (5.36) и (5.37), выбирается наибольшая. Расчетная длина может быть разделена на несколько частей в зависимости от конструктивных особенностей соединения. В таких случаях с учетом непровара к длине каждой части добавляется по 1 см на каждый конец.

 

Расчет винтовых пружин с малым шагом витков

Винтовая пружина представляет собой тонкий стержень, чаще всего круглого сечения, ось которого является винтовой линией. Винтовые пружины применяются в вагонных рессорах и различных деталях машин и механизмов. Для пружин с малым шагом витков (рис.5.38, а) соблюдается условие

                                                                          (5.38)

                                               Рис. 5.38

 

Здесь  - средний диаметр пружины, т.е. диаметр цилиндра, на котором лежит винтовая ось пружины. Таким образом, в этом случае, можно приближенно считать, что плоскость витка горизонтальна. Несмотря на сравнительную сложность формы оси, нетрудно вывести формулы для приближенного расчета пружин с малым шагом. При действии сил, направленных по оси пружины и растягивающих или сжимающих ее, стержень пружины в основном испытывает кручение.

Проведем в каком-либо месте разрез стержня пружины вертикальной плоскостью, проходящей через ось пружины (рис.5.38, б) и отбросим нижнюю часть. При условии (5.38) сечение приближенно можно считать не эллипсом, а кругом.

Действие отброшенной части на верхнюю сводится к силе Р, направленной вверх по оси пружины. При параллельном переносе силы Р в центр сечения стержня (рис.5.38, б) присоединится крутящая пара  Таким образом, в сечении пружины возникают два внутренних силовых фактора: поперечная сила Q=Р и крутящий момент  Оба эти фактора вызывают в сечении касательные напряжения. Наибольшие напряжения от кручения (у контура сечения) будут равны (рис.5.38, г)

                                                 (5.39)

где d – диаметр стержня пружины.

Напряжения от поперечной силы имеют наибольшую величину  вдоль горизонтального диаметра АВ сечения, где они направлены вертикально. По формуле Журавского (рис.5.38, в)

.                                    (5.40)

Внутренняя точка А диаметра является опасной точкой сечения, так как здесь напряжения  и  совпадают по направлению и складываются. Расчетное напряжение будет

             (5.41)

При малом отношении  можно вторым членом в скобках пренебречь по сравнению с единицей, т.е. рассчитывать пружину на одно кручение.

Если же отношение  не мало (например, в вагонных рессорах и других тяжелых пружинах), то влияние поперечной силы на напряжения значительно и должно учитываться. Кроме того, в этом случае существенно сказывается влияние кривизны стержня пружины, вследствие которой напряжение от кручения у внутренней точки А сечения оказывается больше, чем у наружной точки В. Ввиду этого в правую часть формулы (5.41) вместо выражения, стоящего в скобках, лучше ввести коэффициент К, учитывающий одновременно влияние поперечной силы и кривизны стержня:

                                                          (5.42)

Этот коэффициент можно вычислять по формуле

                                                                 (5.43)

где - геометрический параметр пружины.

На практике нужно уметь вычислять удлинение или осадку пружины от растягивающих или сжимающих ее сил. Влияние поперечной силы на удлинение невелико, поэтому обычно принимается в расчет влияние кручения витков.

На рис.5.39 показан бесконечно малый элемент проволоки пружины , находящейся в условиях кручения. Правое сечение поворачивается на угол

а все точки на оси перемещаются на величину

.                                                    (5.44)

Суммируя эти перемещения за счет закручивания длины проволоки, получим полное сокращение расстояния между торцами пружины

     (5.45)

                             Рис. 5.39

 

Условие прочности пружины

                                                  (5.46)

 Так как пружины должны давать достаточно большие упругие удлинения, то они изготовляются из  закаленной стали с очень высоким пределом пропорциональности. Допускаемое касательное напряжение  колеблется при статической нагрузке от 350 МПа до 500 МПа, а для особо прочных специальных сталей – и выше. При переменной нагрузке допускаемое напряжение значительно снижается (на 30-65%).