Лекция 1. Введение

 

Задачи и методы сопротивления материалов

Сопротивление материалов   наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и деталей машин.

Прочность - это способность конструкции сопротивляться разрушению при действии на нее внешних сил (нагрузок).

Жесткость - способность элемента конструкции сопротивляться деформации.

Устойчивость - свойство системы сохранять свое начальное равновесие при внешних воздействиях.

Методами со­противления материалов выполняются расчеты, на основании кото­рых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.

Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Ее экономичность в значительной мере определяется расходом материала, применением менее дефицитных конструкционных материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям. Надежность и экономичность - противоречивые требования.

В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.

В отличие от теоретической механики сопротивление материа­лов рассматривает задачи, в которых наиболее существенными яв­ляются свойства твердых деформируемых тел, а законами движения тела как жесткого целого здесь пренебрегают. В теоретической механике рассматривают равновесие абсолютно твердого (недеформированного) тела, при составлении уравнений равновесия допустимы замена системы сил статически эквивалентной системой, перенос сил вдоль линии их действия, замена ряда сил их равнодействующей. При решении задач сопротивления материалов, подобные замены или перенос сил недопустимы.   

В то же время, вслед­ствие общности основных положений, сопротивление материалов рассматривается как раздел механики твердых деформируемых тел. В состав механики деформируемых тел входят также такие дис­циплины, как: теория упругости, теория пластичности, теория пол­зучести, теория разрушения и др., рассматривающие, по существу, те же вопросы, что и сопротивление материалов. Различие между сопротивлением материалов и другими теориями механики твердо­го деформируемого тела заключается в подходах к решению задач.

Строгие теории механики деформируемого тела базируются на более точной постановке проблем, в связи с чем, для решения задач приходится применять более сложный математический аппарат и проводить громоздкие вычислительные операции. Вследствие этого возможности применения таких методов в практических задачах ограничены.

В свою очередь, методы сопротивления материалов базируются на упрощенных гипотезах, которые, с одной стороны, позволяют решать широкий круг инженерных задач, а с другой, получать при­емлемые по точности результаты расчетов.

При этом главной задачей курса является формирование зна­ний для применения математического аппарата при решении при­кладных задач, осмысления полученных численных результатов и поиска выбора наиболее оптимальных конструктивных решений. То есть данный предмет является базовым для формирования ин­женерного мышления и подготовки кадров высшей квалификации по техническим специализациям.

Сопротивление материалов является основой для изучения курса «Детали машин» и различных специальных дисциплин, таких, как «Конструкция и прочность двигателей», «Конструкция и прочность летательных аппаратов» и т.п. 

Зарождение науки о сопротивлении материалов относится к XVII в. и связано с работами знаменитого ученого того времени Галилео Галилея. Значительный вклад в ее развитие был сделан выдающимися учеными: Гуком, Бернулли, Сен-Венаном, Коши, Ламе, Эйлером и др. В России в конце XIX-начале XX века важные исследования в области сопротивления материалов провели русские ученые Д.И.Журавский, Ф.С.Ясинский, И.Г.Бубнов, С.П.Тимошенко и др.

 

Реальный объект и расчетная схема

В сопротивлении материалов, как и во всякой отрасли естест­вознания, исследование вопроса о прочности или жесткости ре­ального объекта начинается с выбора расчетной схемы. Расчетная схема конструкции  его упрощенная схема, освобожденная от не­существенных в данной задаче особенностей. Например, при расчете на прочность троса, поднимающего груз, можно не учитывать форму груза, сопротивление воздуха, изменение давления и температуры воздуха с высотой, силу тяжести троса и многие другие факторы, учет которых усложняет расчет троса, но практически не влияет на конечный результат. Трос, свитый из большого числа тонких проволочек, в данном примере можно рассматривать как однородный стержень круглого поперечного сечения, нагруженный растягивающей силой, сосредоточенной в месте крепления груза.      

При выборе расчетной схемы вводятся упрощения в геомет­рию реального объекта. Основным упрощающим приемом в сопро­тивлении материалов является приведение геометрической формы тела к схемам бруса, оболочки или пластины. Как известно, любое тело в пространстве характеризуется тремя измерениями. Брусомназывается геометрический объект, одно из измерений которого (длина) много больше двух других. Геометрически брус может быть образован путем перемеще­ния плоской фигуры вдоль некоторой кривой, как это показано на рис. 1.1.

Эта кривая называется осью бруса, а плоская замкнутая фигура, распола­гающая свой центр тяжести на оси бруса и нормальная к ней, называется егопоперечным сечением. Брус может иметь как постоянное, так и переменное поперечное сечение. Многие сложные конструкции на практике рассматриваются как комбинации элементов, имеющих форму бру­са, поэтому в настоящей книге преимущественно рассматриваются методы расчета бруса как основного геометрического объекта изучения науки со­противления материалов. Брус, работающий при растяжении, называется стержнем, при изгибе – балкой, при кручении – валом. Стержневые элементы, воспринимающие вертикальные сжимающие силы, называют стойками, а наклонные элементы - раскосами. Конструкцию, состоящую из соединенных изгибаемых стержней, называют рамой. Если же благодаря шарнирному соединению стержней все они работают только на растяжение или сжатие (от нагрузки, приложенной в узлах), то конструкцию называют фермой.

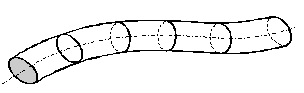
                                           Рис. 1.1

 

Второй основной геометрической фор­мой, рассматриваемой в сопротивлении материалов, является обо­лочка, под которой подразумевается тело, у которого одно из измерений (толщина) намного меньше, чем два других. К оболочкам относятся различного рода резервуары, котлы, купола зданий, корпуса подводных лодок, обшивка фюзеляжа самолета и т.п.

Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной. Примером могут служить крыши и днища резервуаров, перекрытия зданий, различные диски и т.п.

Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга, называется массивом. К ним относятся фундаменты сооружений, подпорные стенки и т.п.

 

Связи и опорные устройства

Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи, ограничивающие перемещения тех точек сооружения, к ко­торым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и дру­гое.

Основным видом связей в расчетной схеме является шарнирная связь.

Простой шарнир (рис. 1.2) накладывает две связи.

 

              Рис. 1.2

 

В расчетную схему входит основание, т.е. тело, на ко­тоpое опирается cистема в целом, считающееся неподвижной.

Неподвижность расчетной схемы относительно основания обеспечивается опорными связями (опорами).

Все опорные связи условно делятся на три основных типа:

- Подвижная шарнирная опора (рис.1.3, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).

- Неподвижная шарнирная опора (рис.1.3, б). Такая опора допускает вращение конца бруса, но устраняет поступательное движение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие, одна из которых направлена вдоль оси бруса (Н), другая - перпендикулярно к оси бруса (R).

- Жесткая заделка или защемление (рис.1.3, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).

При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.

 

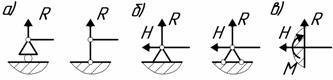
                                             Рис. 1.3

 

 

Внешние и внутренние силы. Метод сечений

Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые на­зываются внешними. Внешние силы, действующие на тело, мож­но разделить на активные (независимые) и реактивные. Реак­тивные усилия возникают в связях, наложенных на тело, и опреде­ляются действующими на тело активными усилиями.

По способу приложения внешние силы делятся на объемные и поверхностные.

Объемные силы распределены по всему объему рассматривае­мого тела и приложены к каждой его частице. В частности, к объ­емным силам относятся собственный вес сооружения, магнитное притяжение  или  силы  инерции.  Единицей  измерения объемных сил является сила, отнесенная к единице объема  кН/м³.

Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рас­сматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки под­разделяются на сосредоточенные и распределенные. К первым от­носятся нагрузки, реальная площадь приложения которых несоиз­меримо меньше полной площади поверхности тела (например, воз­действие колонн на фундаментную плиту достаточно больших раз­меров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Примером может служить собственный вес балки, действие снеговой или ветровой нагрузки на сооружение, давление жидкости в резервуаре. Распределенная нагрузка может действовать и по линии как, например, при соприкасании двух цилиндров при параллельном расположении их осей. Сосредоточенные усилия измеряются в кН, а распределенные  кН/м² или кН/м.

По времени действия внешние нагрузки (силы) разделяются на постоянные и временные. Собственный вес зданий – это постоянно действующая нагрузка; поезд, идущий через мост, - это нагрузка временная. 

По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь.Динамические нагрузки - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию. Динамические нагрузки подразделяются на внезапно приложенные, повторно-переменные и ударные. Примером внезапно приложенной нагрузки может служить действие веса железнодорожного состава, проходящего через мост; повторно-переменной – нагрузка на шатун в двигателе внутреннего сгорания; ударной – действие силы удара молота на его фундамент или гидравлический удар в гидросистеме. Ударные нагрузки возникают также в случае плохой пригонки или износа сопряженных деталей, когда зазоры превышают величину, допустимую по конструктивным и технологическим условиям. Например, при износе зубьев шестерен или деталей шариковых подшипников в машине возникают характерные стуки, свидетельствующие о возникновении ударных нагрузок, быстро приводящих к выходу конструкции из строя. 

Скорость роста усилий при динамическом нагружении не обеспечивает равновесности процессов, протекающих в материале, в результате чего возникают многочисленные нарушения внутренней структуры материала. При систематическом чередовании нагружения и разгрузки накопление дефектов структуры ведет к возникновению микроскопических трещин, слияние которых приводит к усталостному разрушению. 

Взаимодействие между частями рассматриваемого тела характе­ризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмоле­кулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой.

В брусе сечение проводят перпендикулярно его оси. Такое сечение называют поперечным.

Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.

Рассмотрим тело, имеющее форму бруса (рис. 1.4, а).

Пусть к нему приложена некоторая система внешних сил Р₁, Р₂, Р₃,..., Р_n , удовлетворяющая условиям равновесия, т.е. при дейст­вии указанных внешних сил тело находится в состоянии равнове­сия.

Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (P_А ), действующей в сечении А (рис. 1.4, б).

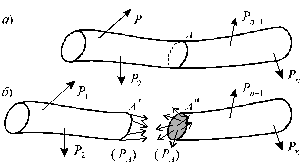
                                           Рис. 1.4

 

Обозначая через  и  суммы внешних сил, приложен­ных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что

                                                                                                                         (1.1)

для отсеченных частей бруса получим следующие очевидные соот­ношения:

; .                                                                                          (1.2)

Последние соотношения показывают, что равнодействующая внутренних сил Р_А в сечении А может определяться с равным успе­хом из условий равновесия либо левой, либо правой частей рассе­ченного тела. В этом суть метода сечений.

Внутренние усилия должны быть так распределены по сече­нию, чтобы деформированные поверхности сечения А при совме­щении правой и левой частей тела в точности совпадали. Это тре­бование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

Воспользуемся правилами статики и приведем систему внут­ренних сил  к центру тяжести сечения А в соответствии с прави­лами теоретической механики. В результате получим главный век­тор сил  и главный вектор момента  (рис. 1.5). Далее выбира­ем декартову систему координат xyz с началом координат, совпада­ющим с центром тяжести сечения А. Ось  направим по нормали к сечению, а оси  и  расположим в плоскости сечения. Спроекти­ровав главный вектор сил  и главный момент  на координат­ные оси x, y, z, получаем шесть составляющих: три силы N_z , Q_x , Q_y и три момента M_z , M_x , M_y , называемых внутренними силовы­ми факторами в сечении бруса.

Составляющая N_z называется нормальной, или продольной си­лой в сечении. Силы Q_x и Q_y называются поперечными усилиями. Момент M_z называетсякрутящим моментом, а моменты M_x и M_y  изгибающими моментами относительно осей x и y, соответственно.

При известных внешних силах все шесть внутренних силовых факторов в сечении определяются из шести уравнений равновесия, которые могут быть составлены для отсеченной части.

Пусть R^*, M^* - результирующая сила и результирующий момент, действующие на отсеченной части тела. Если тело при действии полной системы внешних сил находится в равновесном состоянии, то условия равновесия отсеченной части тела имеет вид:

                                                                                                                             (1.3)

Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:

                                                                                               (1.4)

которые, в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: , , , , , .

                                    Рис. 1.5

 

Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.

В общем случае в сечении могут иметь место все шесть силовых факторов. Однако достаточно часто на практике встречаются случаи, когда некоторые внутренние усилия отсутствуют  такие виды нагружения бруса получили специальные названия (табл.1.1).

                                                                                                                             

Таблица 1.1. Простейшие случаи сопротивления

Вид напряженного состояния	Nz	Qx	Qy	Mz	Mx	My
Растяжение/сжатие	+	0	0	0	0	0
Кручение	0	0	0	+	0	0
Чистый изгиб относительно оси х	0	0	0	0	+	0
Чистый изгиб относительно оси у	0	0	0	0	0	+
Поперечный изгиб относительно оси х	0	0	+	0	+	0
Поперечный изгиб относительно оси у	0	+	0	0	0	+

                                    Примечание: + означает наличие усилия, 0  его отсутствие.

 

Сопротивления, при которых в поперечном сечении бруса дей­ствует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий (например, изгиб с кручением) сопротивление бруса называется сложным.

В заключение заметим, что при выполнении практических рас­четов, для наглядности, как правило, определяются графики функ­ций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изме­нения внутренних усилий вдоль продольной оси стержня называ­ются эпюрами.

 

Напряжения

При определении внутренних силовых факторов их считают приложенными в центре тяжести сечения. В действительности внутренние силы, являясь результатом взаимодействия частиц тела, непрерывно распределены по сечению. Интенсивность этих сил в разных точках сечения может быть различной. При увеличении нагрузки на элемент конструкции увеличиваются внутренние силы и соответственно увеличивается их интенсивность во всех точках сечения. Если в некоторой точке интенсивность внутренних сил достигнет определенного для данного материала значения, в этой точке возникает трещина, развитие которой приведет к разрушению элемента, или возникнут недопустимые пластические деформации. Следовательно, о прочности элементов конструкций следует судить не по значению внутренних силовых факторов, а по их интенсивности. Меру интенсивности внутренних сил называют напряжением.

В окрестности произвольной точки, принадлежащей сечению некоторого нагруженного тела, выделим элементарную площадку , в пределах которой действует внутреннее усилие  (рис. 1.6, а).

Среднее значение интенсивности внутренних усилий на площадке, называемое средним напряжением, определяют по формуле

                                                                                                                      (1.5)

Уменьшая площадь , в пределе получаем истинное напряжение в данной точке сечения

                                                                                                            (1.6)

Векторная величина называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па).

Разложим вектор полного напряжения на две составляющие (рис.1.6, б).

Проекция вектора полного напряжения  на нормаль к данной площадке обознача­ется через  и называется нормальным напряжением.

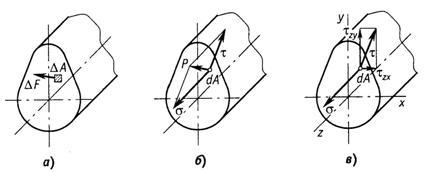
                                                           Рис. 1.6

 

Составляющую, лежащую в сечении в данной площадке обознача­ется через  и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и (рис.1.6, в). Первый индекс при  показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов. 

Между полным напряжением и его составляющими существует зависимость

                                                                                      (1.7)

Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.  

Совокуп­ность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью . По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 1.7)

;  ;  .

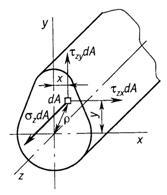
               Рис.1.7

 

Соответствующие элементарные моменты относительно координатных осей , ,  имеют вид:

;   ;    .

Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями:

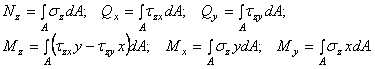                                          (1.8)

В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениями ,  и , выражение для  можно записать в виде

,

где

.

Интегральные зависимости (1.8) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению.

 

Перемещения и деформации

Под действием внешних сил твердые тела изменяют свою гео­метрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор, имеющий свое начало в точке А недефор­мированного состояния, а конец в т. деформированного состоя­ния, называется вектором полного перемещения т. А (рис. 1.8, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, vи w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформиро­ванного состояния, расположенные на расстоянии  друг от друга (рис. 1.8, б).                

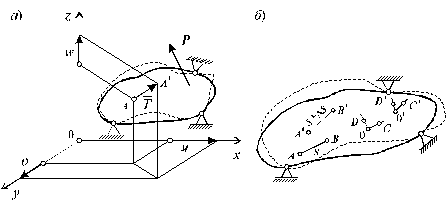
                                                              Рис. 1.8

 

Пусть в результате изменения формы тела эти точки перемес­тились в положение  и , соответственно, а расстояние между ними увеличилось на величину S и составило S + S. Величина

                                                                                                                            (1.9)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей , то в обозначения соответствующих проекций линейной деформации вводятся индексы , , .

Линейные деформации , ,  характеризуют изменения объема тела в процессе деформирования, а формоизменения тела  угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрез­ками ОD и ОС (рис. 1.8, б). При действии внешних сил указанный угол DOCизменится и примет новое значение . Величина

                                                                                         (1.10)

называется угловой деформацией, или сдвигом в точке О в плос­кости СОD. Относительно координатных осей деформации сдвига обозначаются , , .

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформиро­ванное состояние в точке.

 

Закон Гука и принцип независимости действия сил

Многочисленные экспериментальные наблюдения за поведени­ем деформируемых тел показывают, что в определенных диапазо­нах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Р.Гуком и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взя­той точки А (рис. 1.8, а) нагруженного тела по некоторому направ­лению, например, по оси x, а может быть выражено следующим образом:

,                                                                                                                           (1.11)

где Р - сила, под действием которой происходит перемещение u; - коэффициент пропорциональности между силой и перемеще­нием.

Очевидно, что коэффициент  зависит от физико-механиче­ских свойств материала, взаимного расположения точки А и точки  приложения и направления силы Р, а также от геометрических особенностей си­стемы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную за­висимость между напряжениями и деформациями, а не между си­лой и перемещением.

,                                                                                                                                (1.12)

.                                                                                                                                (1.13)

Параметры и , входящие в эти формулы, называют модулями упругости материала соответственно первого и второго рода. Они характеризуют его сопротивляемость деформированию, или жесткость в упругой стадии деформации. Численные значения и  для каждого конструктивного материала определяются экспериментально. Они имеют размерности напряжений. На практике удобно использовать единицы, кратные паскалю: мегапаскаль (1 МПа=10⁶ Па) и гигапаскаль (1 ГПа=10⁹Па). 

Системы, для которых соблюдается условие пропорционально­сти между напряжениями и деформациями, подчиняются принципу суперпозиции, илипринципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе прило­жено несколько сил, то можно определить внутренние силы, на­пряжения, перемещения и деформации от каждой силы в отдель­ности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.

 

Допущения, применяемые в сопротивлении материалов

Для построения теории сопротивления материалов принимают некоторые допущения относительно структуры и свойств материалов, а также о характере деформаций.Приведем основные из них.

1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых суще­ственно превышают не только межатомные расстояния, но и раз­меры кристаллических зерен.

С понятием однородности тесно связано понятие сплошнос­ти среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит в теле конструкции нет пустот. Это допущение позволяет использовать в сопротивлении материалов методы математического анализа (дифференциальное и интегральное исчисления).

2. Обычно сплошная среда принимается изотропной, т.е. пред­полагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево). Отдельно взятый кристалл материалаанизотропен, но т.к. в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристал­лов, принимается, что материал изотропен.

Металлы и сплавы, как правило, изотропны. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе. 

3. Принимается, что до определенной величины деформации материалов подчиняются закону Гука и весьма малы относительно размеров тела, поэтому все расчеты выполняются по исходной, т.е. недеформированной, схеме, к которой применим принцип независимости действия сил.

4. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструк­ций абсолютно упругий. Это допущение справедливо, пока нагрузки не превышают определенного значения. При больших нагрузках в элементах конструкций появляются пластические деформации.

5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции. 

6. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способанагружения.  Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напря­женного состояния и формулируемый следующим образом: осо­бенности приложения внешних нагрузок проявля­ются, как правило, на расстояниях, не превыша­ющих характерных размеров поперечного сечения стержня. Принцип Сен-Венана подробно рассмотрен в части 2.  

7. Принимается гипотеза плоских сечений (гипотеза Бернулли), введенной швейцарским ученым Д. Бернулли, гласящей, что плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.

8. Считается, что ненагруженное тело свободно от каких бы то ни было внутренних сил любой природы.

 

Общие принципы расчета конструкции

В результате расчета нужно получить ответ на вопрос, удовлет­воряет или нет конструкция тем требованиям прочности и жест­кости, которые к ней предъявляются. Для этого необходимо прежде всего сформулировать те принципы, которые должны быть положе­ны в основу оценки условий достаточной прочности и жесткости.

Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъ­являются. Так, наиболее распространенным методом расчета деталей машин на прочность является расчет по допускаемым на­пряжениям. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Расчет выполняется в следующем порядке.

На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие расчетные (рабочие) на­пряжения . Расчетная величина напряжений сопоставляется с пре­дельно допустимой величиной напряжений  для данного материала, полученной на основе предварительных лабораторных испытаний. Чтобы не нарушилась прочность элемента, рабочие напряжения в любой его точке должны быть меньше предельных. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину  принимается . В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается . Для хрупких материалов, а в неко­торых случаях и умеренно пластических материалов, принимается .

 Для надежной работы элемента нельзя допустить, чтобы рабочие (расчетные) напряжения в наиболее напряженной точке были близки к предельным, нужно обеспечить запас прочности.

Отношение предельного напряжения для материала, из которого изготовлен элемент конструкции, к максимальному рабочему напряжению называюткоэффициентом запаса прочности 

.                                                                                                                      (1.14)

Выбор коэффициента запаса прочности – один из основных и наиболее ответственных этапов расчета на прочность. При заниженном коэффициенте запаса прочности снижается надежность работы детали, повышается опасность ее разрушения при эксплуатации. При завышении запаса прочности увеличивается масса и стоимость детали.

Коэффициент  запаса учитывает  следующие  основные факторы.

1. Погрешности в создании рабочей модели.

2. Возможные превышения, нагрузки в процессе эксплуатации.

3. Степень ответственности изделия.

4. Несовершенства в определении свойств материала.

5. Вероятность возможных экстремальных ситуаций  (землетрясение, случайный удар и т.п.).

При назначении коэффициента запаса прочности учитывают, насколько точно можно для проектируемой детали определить рабочее и предельное напряжения. Рабочие напряжения нельзя определить абсолютно точно, так как фактические, действующие на элемент конструкции нагрузки могут существенно отличаться от используемыхв расчете. В процессе эксплуатации конструкции возможно кратковременное увеличение нагрузок (перегрузки), часто нагрузки непрерывно изменяются или носят случайный характер (например, нагрузки на крыло летящего самолета). Формулы сопротивления материалов основаны на определенных допущениях, упрощающих расчеты, и, следовательно, не обеспечивают высокой точности. В деталях сложной формы напряжения, как правило, можно определить только приближенно. Предельные напряжения, характеризующие прочность материала, также нельзя определить абсолютно точно вследствие непостоянства химического состава сплавов в различных плавках, отклонений в режимах технологического процесса изготовления материалов, погрешностей при испытании образцов. При расчете элемента конструкции необходимо учитывать возможные последствия его разрушения.

Так как все факторы, влияющие на прочность элемента конструкции, учесть точно в расчете невозможно, в расчет вводят требуемый (допускаемый) коэффициент запаса прочности , гарантирующий надежную работу элемента конструкции в течение требуемого срока службы (табл.1.2)

 

Таблица 1.2. Ориентировочные значения допускаемого коэффициента

запаса прочности

Вид материала	Характер нагрузки	Коэффициент запаса прочности
Пластичный	Статическая	2,4-2,6
	Ударная	2,8-5,0
	Повторно-переменная	5,0-15,0
Хрупкий	Статическая	3,0-9,0

 

Часто этот коэффициент представляют в виде произведения частных коэффициентов запаса , каждый из которых учитывает влияние на прочность элемента конструкции какого-либо одного ил нескольких факторов.

В каждой отрасли машиностроения существуют нормы на допускаемые запасы прочности, основанные на большом опыте расчета деталей и их эксплуатации. Определяемые по нормам коэффициенты запасы прочности называют нормативными.

Прочность элемента конструкции считают обеспеченной, если расчетный коэффициент запаса не меньше допускаемого

.                                                                                                             (1.15)

Это равенство называют условием прочности.   

Если установлен допускаемый коэффициент запаса прочности и для выбранного материала известно предельное напряжение, определяют максимальное напряжение, которое можно допустить для надежной работы элемента конструкции. Такое напряжение называют допускаемым 

.                                                                                                                     (1.16)

Часто величина допускаемого напряжения берется из таблиц, составленных на основе действующих норм (см. «Справочные данные»).

В практических расчетах  считают, что прочность элемента конструкции обеспечена, если возникающие в нем максимальные напряжения не превышают допускаемых. Условие прочности имеет вид

.                                                                                                                        (1.17)

Если материал имеет различные предельные напряжения при растяжении и сжатии, то допускаемое напряжение обозначают соответственно  и .

Чтобы уточнить, какое напряжение принято в качестве предельного (предел текучести или прочности ), иногда в обозначения расчетных и допускаемых коэффициентов запаса прочности вводят соответствующие индексы: ; ; ; .  

Указанный метод является не единственным. Например, на практике в некоторых случаях используется метод расчета конст­рукций по разрушающим нагрузкам. В этом методе путем расчета определяется предельная нагрузка, которую может выдержать кон­струкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способ­ности конструкции в эксплуатационных условиях.

Условие прочности можно представить в виде

,                                                                                                         (1.18)

где - коэффициент запаса прочности, принимаемый таким же, как и в методе допускаемых напряжений.

При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений  диаграмма Прандтля (рис.1.9). Схематиза­ция диаграммы заключается в предположении, что материал на на­чальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упругопластическим. Такая схема­тизированная диаграмма деформирования в большей степени соот­ветствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам.

Следует заметить, что определение разрушающей нагрузки возможно только для несложных расчетных схем.

                          Рис.1.9

 

Если необходимо добиться наименьших изменений фор­мы конструкции, то производится расчет по допускаемым пе­ремещениям. Это не исключает и одновременной проверки сис­темы на прочность по напряжениям.

В случае расчета конструкции по допускаемым перемещениям необходимо удов­летворять условию

,                                                                                                                                   (1.19)

где  и   максимальное и допускаемое значения переме­щения.

Для расчета строительных конструкций применяется метод расчета по предельным состояниям.

Данный метод предполагает обеспечить такие условия работы конструкции, при которых исключалась бы возможность наступления расчетного предельного состояния, под которым понимают потерю способности сопротивляться внешним силовым воздействиям или отвечать заданным эксплуатационным требованиям.

 

Лекция 2. Осевое растяжение - сжатие

Продольные силы в поперечных сечениях

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы , а прочие силовые факторы равны нулю.

Рассмотрим однородный прямолинейный стержень длиной  и площадью поперечного сечения А, на двух концах которого прило­жены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).

Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).

                      Рис.2.1

 

Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось направим вдоль продольной оси стержня.

Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z () от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:

,

откуда следует, что

.

Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения

                                                                                                                  (2.1)

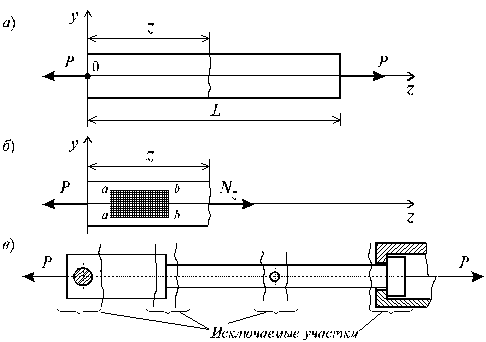
                                                                Рис. 2.2

 

Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Рассмотрим несколько примеров определения внутренних сил.

Пример 1.

Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня, показанный на рис.2.3. Определить величину внутренних сил.

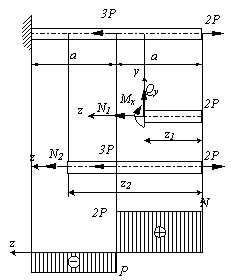
                            Рис.2.3

 

Решение.

Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть,заменяя ее действие внутренними усилиями N, Q_y, M_x и уравновешивая оставшуюся часть, получим:

 участок: 

,  ;

,   ;

, 

Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

 участок: 

,     .

Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось .

Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня (рис.2.3). Построим на первом участке линию параллельную оси z на высоте 2Р, на втором участке – линию со значением -Р. Области ограниченные графиком и осью zпринято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.

 

Пример 2.

Построить эпюру продольных сил для жестко защемленной балки (рис.2.4).

Решение:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.

2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

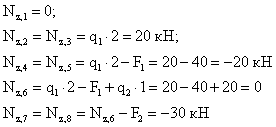
3. По найденным значениям строим эпюру .

Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.

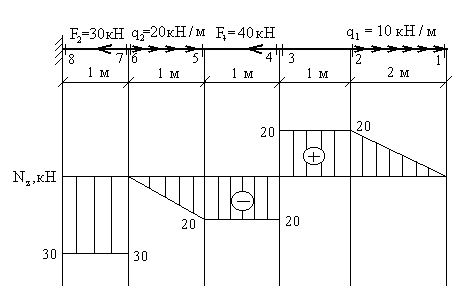
                                                                                    Рис.2.4

 

Пример 3.

Два стержня, соединенные в т. А, находятся под действием силы Р (рис.2.5, а). Определить усилия, действующие в стержнях.

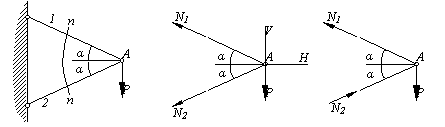
                   а)                                                  б)                                               в)

                                                                   Рис.2.5 

 

Решение.

Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n-n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N₁ и N₂ в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис.2.5, б).

Уравновесим отсеченную часть, запишем уравнения ; .

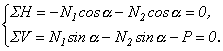
Решая, из первого уравнения получим

,

из второго уравнения окончательно имеем

;     .

Так как величина силы N₂  0, то её направление следует изменить на противоположное (рис.2.5, в). Согласно рисунку нормальная сила N₁ растягивает отсеченную часть стержня 1 - она положительна, сила N₂ сжимает отсеченную часть стержня 2 - она отрицательна.

 

Пример 4.

Абсолютно жесткий брус подвешен на двух стержнях и находится под действием силы Р (рис.2.6, а). Определить усилия в стержнях.

Решение.

Используя метод сечений, получим отсеченную часть, показанную на рис.2.6, б.

Запишем уравнения равновесия  и :

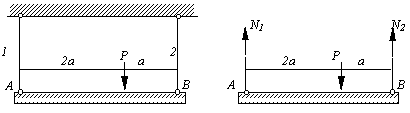
                                                           Рис.2.6

 

Решая систему уравнений, получим

;     .

 

Напряжение в поперечных сечениях стержня

Нормальная сила  приложена в центре тяжести сечения, яв­ляется равнодействующей внутренних сил в сечении и, в соответст­вии с этим, определяется следующим образом:

.

Но из этой формулы нельзя найти закон распределения нор­мальных  напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямо­угольную сетку (рис. 2.2, б), то после нагружения поперечные ли­нии аа, bb и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что по­перечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).

Значит, все продольные волокна стержня находятся в одина­ковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и рав­ны

,                                                                                                                          (2.2)

где A  площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 2.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения , одинаковы:  (рис. 2.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 2.7, в).          

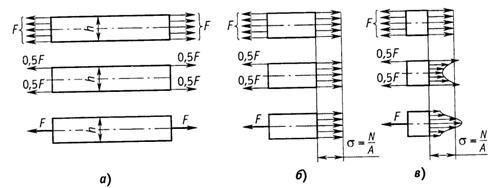
Рис.2.7

 

Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения пло­щади поперечного сечения (рис. 2.2, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.

Нормальные напряжения при сжатии определяют также, как и при растяжении, но считают отрицательными.

Следует помнить, что длинные (тонкие) стержни, нагруженные сжимающими силами, могут потерять устойчивость. Расчет стержней на устойчивость рассмотрен в разделе «Устойчивость». 

В инженерных сооружениях встречаются растянутые или сжатые элементы, имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные напряжения по формуле

,                                                                                                                        (2.3)

где   площадь поперечного сечения нетто; - площадь поперечного сечения брутто; - площадь его ослабления.

 

Деформации и перемещения. Закон Гука

Рассмотрим однородный стержень с одним концом, жестко за­деланным, и другим - свободным, к которому приложена централь­ная продольная сила Р (рис. 2.8). До нагружения стержня его длина равнялась  - после нагружения она стала равной  (рис. 2.8). Величину  называют абсолютным удлинением стержня.

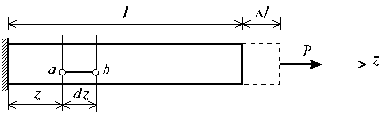
                                                    Рис. 2.8

 

Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых ус­ловиях, деформация  остается одной и той же по длине стержня и равной

.                                                                                                                                            (2.4)

Если же по длине стержня возникает неоднородное напряжен­ное состояние, то для определения его абсолютного удлинения не­обходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.8). При растяжении он увеличит свою длину на величину  и его деформация составит:

.                                                                                                                                        (2.5)

В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации ):

.                                                                                                                                           (2.6)

Величина Е представляет собой коэффициент пропорциональ­ности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.

Из совместного рассмотрения уравнений (2.5) и (2.6) получим:

,

откуда с учетом того, что

 и ,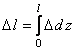

окончательно получим:

.                                                                                                                                (2.7)

Если стержень изготовлен из однородного изотропного мате­риала с Е = const, имеет постоянное поперечное сечение A = const и нагружен по концам силой Р, то из (2.7) получим

.                                                                                                                                       (2.8)

Зависимость (2.8) также выражает закон Гука. Знаменатель EA называется жесткостью при растяжении - сжатии или продольной жесткостью.

При решении многих практических задач возникает необходи­мость, наряду с удлинениями, обусловленными действием механи­ческих нагрузок, учитывать также удлинения, вызванные темпера­турным воздействием. В этом случае пользуются принципом неза­висимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:

,                                                                                                                                   (2.9)

где   коэффициент температурного расширения материала; t пе­репад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:

.                                                                                                                           (2.10)

 

Потенциальная энергия деформации

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу W на соответству­ющих перемещениях. Одновременно с этим в упругом теле накап­ливается потенциальная энергия его деформирования U. При дей­ствии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

W = U + K.                                                                                                                                         (2.11)

При действии статических нагрузок К = 0, следовательно,

W = U.                                                                                                                                                 (2.12)

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформа­ции. При разгрузке тела производится работа за счет потенциаль­ной энергии деформации, накопленной телом. Таким образом, уп­ругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружи­нах часовых механизмов, в амортизирующих рессорах и др. В слу­чае простого растяжения (сжатия) для вывода необходимых расчет­ных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.

На рис. 2.9, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку , ниже показан график изменения величины удлинения стержня  в зависимости от силы Р (рис. 2.9, б). В соответствии с законом Гука этот график носит линейный характер.

Пусть некоторому значению силы Р соответствует удлинение стержня . Дадим некоторое приращение силе Р  соответству­ющее приращение удлинения составит . Тогда элементарная работа на этом приращении удлинения составит:

,                                                             (2.13)

                                                                         Рис.2.9

               

вторым слагаемым, в силу его малости, можно пренебречь, и тогда

.                                                                                                                              (2.14)

Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка  перемещение”, работа внешней силы Р на перемещении  будет равна площади треугольника ОСВ (рис. 2.9), т.е.

.                                                                                                                                 (2.15)

В свою очередь, когда напряжения  и деформации  распреде­лены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:

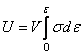.                                                                                                                                    (2.16)

Поскольку, в данном случае имеем, что ,  и , то

,                                              (2.17)

т.е. подтверждена справедливость (2.12).

С учетом (2.8) для однородного стержня с постоянным попе­речным сечением и при Р = const из (2.17) получим:

.                                                                                                                                         (2.18)

Единицей измерения потенциальной энергии деформации является 1Hм = 1Дж.

 

Напряженное и деформированное состояние при растяжении и сжатии

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол  с плоскостью нормального сечения (рис. 2.10, а).

Из условия , записанного для отсеченной части стержня (рис. 2.10, б), получим:

,                                                                                                                                             (2.19)

где A  площадь поперечного сечения стержня,   пло­щадь наклонного сечения. Из (2.19) легко установить:

.                                                                                                                                           (2.20)

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 2.10, в), с учетом (2.20) получим:

;     .                                                 (2.21)

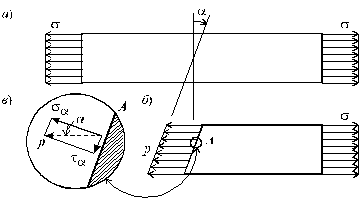
                                                        Рис. 2.10

 

Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла . При  из (2.21) следует, что , . При , т.е. на продольных площадках, . Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения  принимают наибольшие зна­чения при , и их величина составляет . Важно отме­тить, что . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит назва­ние закона парности касательных напряжений.

Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направ­лении сопровождается пропорциональным уменьшением попереч­ных размеров стержня (рис. 2.11).

Если обозначить:

;     ;     ,

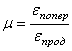то, как показывают эксперименты,  = const для данного материала и является безразмерным коэффициентом Пуассона. Вели­чина  является важной характеристикой материала и определяется экспериментально. Для реальных материалов  принимает значе­ния 0,1...0,45.

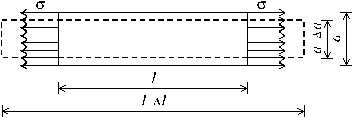
                                                           Рис. 2.11

 

При растяжении стержня возникают не только линейные, но и угловые деформации.

Рассмотрим прямой угол АВС (рис. 2.12, а), образованный отрез­ками АВ и АС, в недеформированном состоянии.

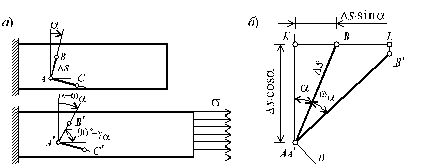
                                                         Рис. 2.12

 

При растяжении стержня точки А, В и С займут положение А, B, C соответственно. Величина

называется угловой деформацией или угловым сдвигом в точке А.

Совместим точки А и А и рассмотрим взаимное расположение отрезков АВ и АB (рис. 2.12, б). На этом рисунке отметим вспомо­гательные точки K и L и прямую n, перпендикулярную отрезку АB. Из рис. 2.12, б имеем:

;     ,

откуда с учетом  получим:

  .                                                                           (2.22)

Для определения  спроектируем ломаную  на ось n

 ,

откуда, учитывая ма­лость угла , т.е. , , получим:

.                                                                                                      (2.23)

В результате совместного рассмотрения (2.22) и (2.23) получим:

.

Откуда .

Следовательно, .                                                  (2.24)

Сопоставляя выражение  с выражением  из (2.21) окон­чательно получим закон Гука для сдвига:

                                                                                                                                               (2.25)

где величина  называется модулем сдвига или модулем упругости материала второго рода.

 

Расчеты на прочность и жесткость при растяжении (сжатии)

Основной задачей расчета конструкции является обеспечение ее безопасной эксплуатации. Важнейшим условием, обеспечивающим безопасную эксплуатацию конструкции, является условие прочности. Существуют различные методы обеспечения прочности конструкций. Мы чаще всего будем пользоваться одним из этих методов – расчетом по допускаемым напряжениям. Согласно этому методу для конструкций, работающих на растяжение-сжатие, условие прочности, составленное для опасного сечения,  можно записать в таком виде:

                                                                                                        (2.26)

где  – максимальное напряжение в конструкции; – характеристика материала, называемая допускаемым напряжением.

Допускаемое напряжение находится по формуле

.                                                                                                                                   (2.27)

где  – предельное напряжение, при достижении которого в стержне наступает предельное состояние материала: появляются пластические деформации, если материал стержня – пластичный, или происходит разрушение, если стержень выполнен из хрупкого материала; n – нормируемый коэффициент запаса прочности.

Кроме формулы (2.26), возможен второй вариант условия прочности

,                                                                                                                                            (2.28)

где                                                                                                                 (2.29)

называется действительным коэффициентом запаса прочности, показывающим во сколько раз надо увеличить максимальное напряжение в стержне, чтобы материал стержня оказался в опасном (предельном) состоянии.

Условие прочности в зависимости от цели поставленной задачи позволяет выполнять расчеты на прочность двух видов: проектный и проверочный. Для спроектированного стержня можно также определять допускаемую нагрузку.

Проектный расчет выполняют с целью определения размеров поперечных сечений элемента конструкции при известных рабочих нагрузках и материале (допускаемых напряжений). Площадь поперечного сечения определяют из выражения

.                                                                                                                                            (2.30)

Форма сечения стержня не влияет на его прочность при растяжении (сжатии). Форму сечения стержня необходимо знать только для определения размеров сечения при известном значении площади.

Зная площадь сечения и его форму, находят размеры сечения.

Проверочный расчет выполняют для спроектированной конструкции с целью проверки ее прочности. При проверочном расчете должны быть известны площадь опасного сечения, нагрузка и материал (допускаемое напряжение). Проверочный расчет выполняют по формуле (2.26).

Определение допускаемой нагрузки для спроектированного элемента конструкции, размеры поперечного сечения которого и материал (допускаемые напряжения) известны. Условие прочности в этом случае записывают в виде

.                                                                                                                                          (2.31)

Зная значение , определяют допускаемую нагрузку .

Так как допускаемые напряжения не имеют точного значения, а выбираются приближенно, то при проверочном расчете максимальные рабочие напряжения могут превышать допускаемые на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки так, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки та, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%.

При проектировании элементов конструкций стремятся сделать их во всех сечениях равнопрочными.

Рассмотренные три вида расчетов на прочность можно выполнять не только при растяжении или сжатии, а при любом виде деформации (сдвиге, кручении, изгибе).

При проектировании строительных конструкций расчет на прочность стальных элементов, подверженных центральному растяжению или сжатию, следует выполнять по формуле

                                                                                                                                      (2.32)

где – коэффициент условий работы, принимаемый по СНИП (см. табл.2.1) или другим нормам.

                                                                                                                                                    Таблица 2.1

Элементы конструкции

Колонны общественных зданий и опор водонапорных башен Элементы стержневых конструкций покрытий и перекрытий: а) сжатых при расчетах на устойчивость б) растянутых в сварных конструкциях Сплошные составные балки, колонны, несущие статическую нагрузку и выполненные с помощью болтовых соединений, при расчетах на прочность Сечения прокатных и сварных элементов, несущих статическую нагрузку, при расчетах на прочность Сжатые элементы из одиночных уголков, прикрепляемые одной полкой

0,95     0,95 0,95     1,1   1,1   0,75

                                              Примечание: В случаях, не оговоренных в настоящих нормах, в формулах следует

                                                               принимать  .

 

Для хрупких строительных материалов условия прочности принимают вид:

при растяжении: , ;

при сжатии: ,                                                                                    (2.33)

где  и  – допускаемые напряжения при растяжении и сжатии; n_t и n_c – нормативные коэффициенты запаса прочности по отношению к пределу прочности (n_t, n_c>1).

Для центрально сжатых бетонных элементов формула (2.33) записывается в виде:

                                                                                                                                         (2.34)

где  – коэффициент, принимаемый для бетона тяжелого, мелкозернистого и легкого равным 1,00; для ячеистого автоклавного – 0,85; для ячеистого неавтоклавного – 0,75.

В некоторых случаях работоспособность элемента конструкции определяется не только его прочностью, но и жесткостью, т.е. способностью элемента воспринимать нагрузки без недопустимых упругих деформаций. При расчетах на жесткость определяют максимальные перемещения сечений и сопоставляют их с допускаемыми перемещениями.

Условие жесткости, ограничивающее изменение длины элемента, имеет сле­дующий общий вид:

,

где  - изменение размеров детали;

 - допускаемая величина этого изме­нения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин   по участкам

,                                                                                                                                        (2.35)

условие жесткости при растяжении (сжатии) запишем следующим образом:

.                                                                                                                         (2.36)

Так как перемещение, согласно закону Гука, зависит от нагрузки и размеров поперечного сечения, условие жесткости позволяет решать те же три вида задач, что и условие прочности.  

 

Расчеты статически определимых стержней

Статически определимый стержень – это стержень, который можно рассчитать, используя только уравнения равновесия (уравнения статики).

В любой науке, которая называется «точной» и в которой используются аналитические методы описания состояний и явлений, не обойтись без моделей. В нашем случае при решении различных задач мы каждый раз будем выбирать для рассматриваемого объекта расчетную схему.

Расчетная схема – это упрощенная схема конструкции или ее элементов, освобожденная от несущественных в данной задаче особенностей. При этом расчетная схема должна отражать все наиболее существенное для характера работы данной конструкции и не содержать второстепенных факторов, мало влияющих на результаты ее расчета. Построение и обоснование расчетной схемы – ответственный этап проектирования и расчета конструкции.

Перейдем к рассмотрению конкретных примеров.

 

Пример 5.

Чугунная труба-стойка высотой  с наружным диаметром  и внутренним диаметром  нагружена сжимающей силой , модуль упругости чугуна . Найти напряжение  в поперечном сечении колонны, абсолютное  и относительное укорочения .

Решение.

Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной , жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 2.13, а.

Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая продольная сила .

                                                                      Рис. 2.13.

 

Максимальное нормальное напряжение  определяется по формуле:

                                                                              

где  – площадь трубы:

.

тогда:

Абсолютное и относительное укорочения стойки определяем по формулам:

Знак "минус" обозначает уменьшение размера (укорочение).

 

Пример 6.

Стальной стержень круглого сечения растягивается усилием . Относительное удлинение не должно превышать , а напряжение –. Найти наименьший диаметр, удовлетворяющий этим условиям, если модуль упругости стали .

Решение.

Как и ранее, решение задачи начинается с изображения расчетной схемы и построения эпюра продольных сил (рис. 2.14).

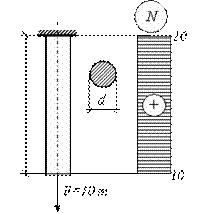
                           Рис.2.14

 

По условию задачи напряжение не должно превышать , в связи с чем данная величина может быть принята за расчетное сопротивление материала стойки на растяжение, то есть . По аналогии заданное относительное удлинение можно принять за предельно допустимое для данной стойки, то есть . В результате необходимо подобрать диаметр стойки, удовлетворяющий условию прочности и условию жесткости.

Продольное растягивающее усилие  равно по величине внешней нагрузке, действующей на стержень 

Требуемая площадь поперечного сечения колонны из условия прочности будет определяться выражением:

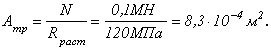
Зная требуемую площадь, выразим необходимый из условия прочности диаметр:

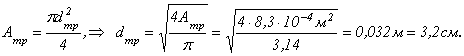
Условие жесткости при центральном растяжении-сжатии:

            

                                                  

Выражаем из предельного неравенства требуемую из условия жесткости площадь поперечного сечения:

Диаметр стойки из условия жесткости определим по формуле:

Окончательно принимаем из двух диаметров больший, 

 

Пример 7.

Определить грузоподъемность и удлинение балки, если .

Расчетная схема бруса и эпюра продольных сил изображены на рис. 2.15.

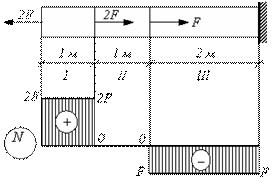
                                       Рис.2.15

 

Решение.

Грузоподъемность бруса – это максимальная нагрузка, которую он может выдержать, не разрушаясь. Таким образом, необходимо определить требуемую нагрузку из условия прочности:

                                                   

Согласно эпюре , тогда условие прочности примет вид:

                                                                           

Отсюда грузоподъемность бруса будет равна:

                                                                                       

Для определения удлинения стержня  разбиваем его на участки. Каждый участок, должен иметь постоянную жесткость  и величину продольной силы. Таким образом, для данного бруса получаем три участка (на рис. 2.15 они обозначены римскими цифрами), тогда абсолютная деформация в общем виде будет определяться выражением:

,  

в котором каждое слагаемое определяется отдельно:

                

где  - значения продольных сил соответственно на первом, втором и третьем участках;  - длины соответственно первого, второго и третьего участков;  - значения модулей упругости материалов бруса для каждого участка;  - площади поперечных сечений стержня на первом, втором и третьем участках.

Поскольку жесткости всех трех участков одинаковые (балка изготовлена из одного материала и имеет постоянное по всей длине поперечное сечение), можно обозначить  и вынести этот множитель за скобки. В результате получим выражение в виде:

где , , , , .

 

Пример 8.

Проверить прочность чугунного бруса (рис.2.16, а). Принять =150 МПа; =650 МПа, допускаемый коэффициент запаса прочности = 4.  

Решение.

Строим эпюры продольных сил и нормальных напряжений  (рис.2.16, б и в).

                                     Рис.2.16

 

Напряжения на участках бруса

Так как материал бруса имеет различную прочность при растяжении и сжатии, проверку прочности следует выполнять для сжатого и растянутого участков, несмотря на то, что на участке напряжение значительно больше по абсолютному значению.

Коэффициенты запаса прочности

 

- прочность обеспечена;

 

- прочность обеспечена.

Из решения задачи можно сделать следующие выводы:

1) прочность стержня не обеспечена, так как на одном его участке коэффициент запаса прочности меньше требуемого;

2) на участках и  коэффициент запаса прочности завышен, следовательно, эти участки бруса можно сделать меньшего диаметра. При проектировании элементов конструкций следует стремиться к тому, чтобы во всех сечениях коэффициент запаса прочности был равен или близок к требуемому.

Проверку прочности бруса можно было выполнить, используя условие прочности в виде , определив предварительно допускаемые напряжения по формулам

;     .

 

Учет собственного веса при растяжении и сжатии

Подбор сечений с учетом собственного веса (при растяжении и сжатии)

При установлении внешних сил, растягивающих или сжимающих элементы конструкций, мы до сих пор игнорировали собственный вес этих элементов. Возникает вопрос, не вносится ли этим упрощением расчета слишком большая погрешность? В связи с этим подсчитаем величины напряжений и деформаций при учете влияния собственного веса растянутых или сжатых стержней.

Пусть вертикальный стержень (рис.2.17, а) закреплен своим верхним концом; к нижнему его концу подвешен груз Р. Длина стержня l, площадь поперечного сечения F, удельный вес материала  и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии  от свободного конца стержня.

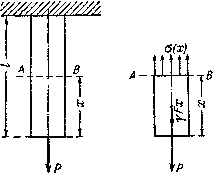
               а)                                       б)

                            Рис.2.17.

 

Рассечем стержень сечением АВ и выделим нижнюю часть длиной с приложенными к ней внешними силами (рис.2.17, б) — грузом Р и ее собственным весом . Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределенными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна:

Таким образом, при учете собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряженным, опасным, будет верхнее сечение, для которого  достигает наибольшего значения l; напряжение в нем равно:

Условие прочности должно быть выполнено именно для этого сечения:

Отсюда необходимая площадь стержня равна:

От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина .

Чтобы оценить значение этой поправки, подсчитаем ее для двух случаев. Возьмем стержень из мягкой стали длиной 10 м; для него, а величина. Таким образом, для стержня из мягкой стали поправка составит  т. е. около 0,6%. Теперь возьмем кирпичный столб высотой тоже 10 м; для него, а величина  Таким образом, для кирпичного столба поправка составит 18/1,2, т.е. уже 15%.

Вполне понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчете длинных канатов подъемников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчет и собственный вес конструкции.

В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберем сечение стержня так, что дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нем дойдет до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так запроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны,

Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.

Возьмем длинный стержень, подверженный сжатию силой Р и собственным весом (рис.2.18). Чем ближе к основанию стержня мы будем брать сечение, тем больше будет сила, вызывающая напряжения в этом сечении, тем большими придется брать размеры площади сечения. Стержень получит форму, расширяющуюся книзу. Площадь сечения F будет изменяться по высоте в зависимости от  , т. е. .

Установим этот закон изменения площади в зависимости от расстояния сечения  от верха стержня.

 

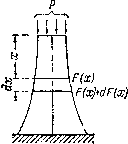                         Рис.2.18.

 

Площадь верхнего сечения стержня  определится из условия прочности:

и 

где — допускаемое напряжение на сжатие; напряжения во всех прочих сечениях стержня также должны равняться величине

Чтобы выяснить закон изменения площадей по высоте стержня, возьмем два смежных бесконечно близких сечения на расстоянии  от верха стержня; расстояние между сечениями ; площадь верхнего назовем , площадь же смежного .

Приращение площади  при переходе от одного сечения к другому должно воспринять вес элемента стержня между сечениями. Так как на площади он должен вызвать напряжение, равное допускаемому , то определится из условия:

Отсюда:

После интегрирования получаем:

При  площадь ; подставляя эти значения, имеем:

и 

Отсюда

, 

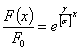
Если менять сечения точно по этому закону, то боковые грани стержня получат криволинейное очертание (рис.2.18), что усложняет и удорожает работу. Поэтому обычно такому сооружению придают лишь приближенную форму стержня равного сопротивления, например в виде усеченной пирамиды с плоскими гранями. Приведенный расчет является приближенным. Мы предполагали, что по всему сечению стержня равного сопротивления передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности.

В случае длинных канатов или растянутых штанг форму стержня равного сопротивления осуществляют тоже приближенно, разделяя стержень по длине на ряд участков; на протяжении каждого участка сечение остается постоянным (рис.2.19) — получается так называемый эквивалентный ступенчатый стержень.

 

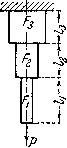                                     Рис.2.19.

 

Определение площадей , ... при выбранных длинах производится следующим образом. Площадь поперечного сечения первого нижнего участка будет по формуле равна:

Чтобы получить площадь поперечного сечения второго участка, надо нагрузить его внешней силой Р и весом первого участка :

Для третьего участка к внешней силе добавляются веса первого и второго участков. Подобным же образом поступают и для других участков.

 

Деформации при действии собственного веса

При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной , находящегося на расстоянии  от конца стержня (рис.2.20).

 

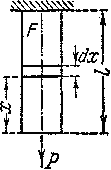                         Рис.2.20.

 

Абсолютное удлинение этого участка равно

Полное удлинение стержня  равно:

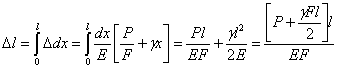
Величина представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:

подразумевая под S внешнюю силу и половину собственного веса стержня.

Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым , относительное удлинение по всей длине стержня одинаково и равно

Абсолютное же удлинение при длине стержня l равно:

Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.

 

Пример 9.

Определить объем кладки мостовой опоры высотой 42 м, нагруженной сжимающей силой F=400 т, для двух вариантов:

1 вариант - опора постоянного сечения;

2 вариант - опора ступенчатая из трех частей одинаковой высоты.

Объемный вес материала кладки , расчетное сопротивление материала кладки на сжатие .

Решение.

Объем кирпичной кладки вычисляется по формуле:

,                                                                                       

где  - площадь поперечного сечения столба;  - высота столба.

Таким образом, для решения задачи необходимо знать площади поперечных сечений мостовой опоры.

1.ВАРИАНТ. Расчетная схема и эпюра внутренних усилий  для данного варианта изображена на рис. 2.21.

                                      Рис.2.21

 

Максимальная сжимающая продольная сила возникает у основания опоры и определяется выражением (для удобства будем подставлять значения внутренних усилий по абсолютной величине):

                                                                   

                                                    

Записываем условие прочности:

                                                                                 

Подставляя в это выражение значение  получим:

                                                                   

Отсюда требуемая площадь из условия прочности кладки на сжатие равна:

Объем кладки для первого варианта будет равен:

2 ВАРИАНТ. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.22.

Мостовая опора состоит из трех ступеней, высота каждой . Площади поперечных сечений ступеней соответственно , , , в связи с чем в пределах каждой ступени от действия собственного веса будут возникать различные по величине продольные силы и напряжения.

Таким образом, для решения задачи необходимо рассмотреть условие прочности для каждой ступени отдельно.

                                                           Рис.2.22

 

1-я ступень. Максимальная сжимающая продольная сила для первой ступени (рис. 2.22):

.

По аналогии с вариантом 1, записываем для первой ступени условие прочности и подставляем в него исходные данные:

.

Отсюда требуемая площадь первой ступени равна:

2-я ступень. Максимальная сжимающая продольная сила для второй ступени (рис. 2.22):

.

Записываем для второй ступени условие прочности и подставляем в него исходные данные:

.

Отсюда требуемая площадь второй ступени равна:

3-я ступень. Максимальная сжимающая продольная сила для третьей ступени (рис. 2.22):

.

Записываем для третьей ступени условие прочности, из которого по аналогии с предыдущими записями определяем требуемую площадь поперечного сечения:

Объем кладки мостовой опоры для второго варианта определяется выражением:

.

Таким образом, мостовая опора, состоящая из ступеней различной площади, выгоднее по расходу материала, чем опора постоянного по всей высоте сечения.

 

Пример 10.

Определить полное удлинение стержня, с учетом собственного веса, а также перемещение сечения m-n. Площадь поперечного сечения – А, модуль упругости – Е, объемный вес материала -  Расчетная схема стержня изображена на рис. 2.23.

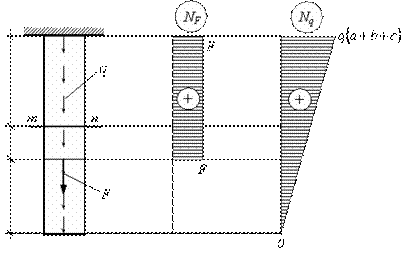
                                               Рис.2.23

 

Решение.

Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы  и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки . Расчетная схема и эпюры продольных сил  и  изображены на рис. 2.23.

Полное удлинение стержня  будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы  и от действия собственного веса:

.

Или в другом виде:

.    

Для того, чтобы определить перемещение сечения m-n отбрасываем часть стержня ниже сечения m-n, а ее действие заменяем сосредоточенной силой , равной продольной силе в сечении m-n:

.

В результате получаем новую расчетную схему, которая приведена на рис. 2.24.

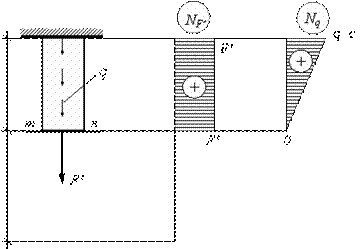
                                          Рис.2.24.

 

А теперь решаем новую задачу о нахождении полного удлинения  уже для данного стержня (рис. 2.23):

,

.

 

Расчет статически определимых стержневых систем

Статически определимая стержневая система – это система, в которой все неизвестные реакции опор и внутренние усилия можно определить из уравнений равновесия (статики).

Для «решения» любой стержневой системы необходимо выделить в ней объект равновесия. В связи с этим, все системы можно разделить на два типа:

1 тип – системы, состоящие из абсолютно жестких (недеформируемых) стержней и одиночных невесомых (деформируемых) стержней. Для стержневых систем этого типа объектами равновесия являются недеформируемые стержни.

2 тип – системы, состоящие из нескольких деформируемых стержней, соединенных в одной точке. Точки соединения двух и более стержней называются узлами, которые и являются объектами равновесия для систем 2-го типа.

Все соединения в элементах систем шарнирные, однако существуют определенные правила, по которым вводятся реакции и усилия в стержнях:

- в шарнире, соединяющем абсолютно жесткий элемент системы с «землей» или с другой конструкцией, всегда возникают две реакции – горизонтальная  и вертикальная ;

- в шарнире, соединяющем деформируемый стержень с абсолютно жестким стержнем или с другой конструкцией, всегда возникает одна реакция, направленная вдоль этого стержня и равная по величине усилию, возникающему в нем.

В абсолютно жестких стержнях никогда не возникает внутренних усилий, они не деформируются!

- в шарнире, соединяющем несколько деформируемых стержней (узловой шарнире), возникают усилия, направленные вдоль этих стержней и сходящиеся в этом узле.

Порядок решения большинства задач о проверке прочности статически определимых стержневых систем при расчете по допускаемым напряжениям сводится к следующим этапам:

1) находим внутренние усилия (продольную силу при растяжении-сжатии) и выявляем опасные сечения;

2) определяем напряжения;

3) после выявления максимальных напряжений используем условие прочности (формулы (2.26), (2.28), (2.32)) при растяжении-сжатии).

 

Пример 11.

Абсолютно жесткий брус  поддерживается стальным стержнем , имеющим площадь поперечного сечения 100 мм² (рис.2.25, а). Определить из условия прочности стержня допускаемую нагрузку  и проверить, обеспечена ли жесткость системы, если допускается перемещение сечения  бруса под действием силы  не более 2 мм. Допускаемое напряжение принять равным =150 МПа, модуль упругости Па.  

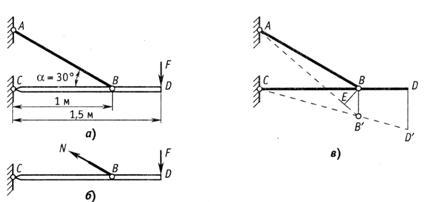
                                                                    Рис.2.25

 

Решение.

Используя метод сечений, определим соотношение между продольной силой  в стержне  и нагрузкой . Из условия равновесия сил (рис.2.25, б) находим

;  ;   .

Допускаемая продольная сила  для стержня  из условия его прочности

Допускаемая нагрузка на систему

При нагружении системы стержень  удлиняется на , а абсолютно жесткий брус поворачивается, оставаясь прямолинейным. Система после деформации стержня  показана штриховой линией на рисунке 2.25, в. Из треугольника  определяем длину  стержня : м.

На основании принципа начальных размеров принимаем, что значение угла  не изменяется, а точки и  перемещаются по вертикали.

Из прямоугольного треугольника находим

; так как ,  , то

Перемещение точки  определяем из подобия треугольников  и  

;    

Жесткость системы не обеспечена.

Следует заметить, что нельзя повысить жесткость системы, применив для стержня  более прочную сталь, так как характеристикой свойств материала, влияющей на жесткость, является модуль упругости, значение которого для всех марок сталей примерно одинаково. Повысить жесткость системы можно, либо увеличив площадь поперечного сечения стержня , либо уменьшив его длину.

 

Пример 12.

Определить допускаемую нагрузку  для системы из двух стержней, изготовленных из дюралюминиевых труб одинакового поперечного сечения (рис.2.26, а). Допускаемое напряжение принять = 100 МПа.  

                                                                            Рис.2.26

 

Решение.

Используя метод сечений, вырезаем узел  и из уравнений равновесия сил

;   ;

;   

находим неизвестные продольные силы, возникающие в стержнях, через нагрузку (рис.2.26, б)

;    .

Допускаемую нагрузку  определяем из условия прочности наиболее нагруженного стержня 1: 

Следует отметить, что стержень 2 недогружен. Напряжение в нем

что примерно на 30% ниже допускаемого. Для стержня 2 можно использовать трубу меньшего поперечного стержня.

 

Пример 13.

Рассмотрим стержневую систему, состоящую из абсолютно жесткого (недеформируемого) стержня , шарнирно закрепленного в точке  и невесомого (деформируемого) стержня , шарнирно закрепленного по концам, загруженную в точке  сосредоточенной силой  (рис. 2.27).

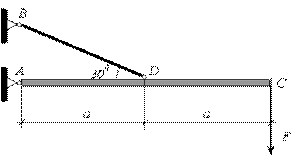
                                    Рис.2.27

 

Решение.

Объектом равновесия в данном случае будет являться стержень , для которого и будем составлять уравнения равновесия.

Под действием внешней нагрузки, на основании введенных выше правил, в точке будут возникать две реакции  и , а в стержне  возникает усилие , направленное по стержню (рис. 2.28).

Определим несущую способность (грузоподъемность) заданной системы, то есть допустимую нагрузку , если площадь сечения стержня , расчетное сопротивление материала стержня .

Для этого можно составить следующие уравнения равновесия:

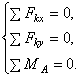
                                              Рис.2.28

 

Поскольку в конечном итоге решение задачи будет сводиться  к определению усилия в стержне , то оставляем в рассмотрении уравнение равновесия, содержащее только , то есть уравнение моментов относительно точки . Распишем данное уравнение:

отсюда неизвестное усилие

.

Записываем условие прочности для стержня и выражаем нагрузку :

,

.

 

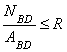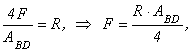
Пример 14.

Определить необходимые размеры поперечных сечений металлических тяг в стержневой системе из условия прочности, если тяга № 1 – из стали, расчетное сопротивление , поперечное сечение - швеллер; тяга № 2 – из алюминия, расчетное сопротивление , круглого поперечного сечения. Стержневая система изображена на рис. 2.29.

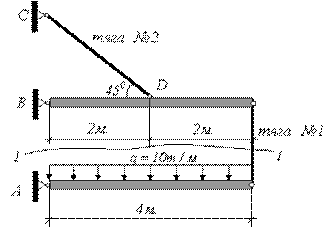
                                     Рис.2.29

 

Решение.

Под действием внешней нагрузки в точках опор системы ,  и  возникают реакции , , , , , . Кроме того, в тягах возникают усилия соответственно  и .

Для решения данной задачи необходимо по очереди рассмотреть равновесие двух абсолютно жестких стержней. Сначала рассекаем систему сечением 1-1 по тяге № 1 и рассматриваем равновесие нижнего бруса (рис. 2.30, б), а затем - равновесие верхнего бруса (рис. 2.30, а). Из условий равновесия для нижней части будем находить усилие в первой тяге , а из условия равновесия для верхней -  (при этом усилие  считается уже известным).

Для определения усилия  необходимо записать уравнение моментов относительно точки  (рис. 2.30, б):

отсюда  - усилие растяжения.

Теперь, считая усилие  известным, необходимо рассмотреть равновесие средней части, для чего записать уравнение моментов относительно точки  (рис. 2.30, а):

.

отсюда  - усилие растяжения.

а)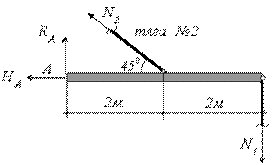

б)

                                          Рис.2.30

 

Далее, для каждой тяги записываем условие прочности и выражаем площади поперечных сечений  - площадь тяги № 1,  - площадь тяги № 2.

ТЯГА № 1:

,

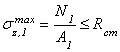По сортаменту принимаем швеллер  [ №10,  

Фактическая площадь сечения должна быть не меньше требуемой!

ТЯГА № 2:

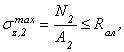
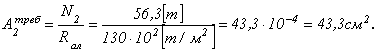
Алюминиевая тяга имеет круглое сечение, тогда требуемый диаметр:

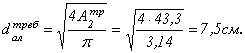
Фактическая площадь круглого сечения:

 

Пример 15.

Определить усилия, возникающие в стержнях системы (рис. 2.31) под действием внешней нагрузки.

                                    Рис.2.31

 

Решение.

Под действием внешней нагрузки в точке опоры системы А возникают реакции , , а также усилия в стержнях , , .

В качестве объектов равновесия в этой задаче выступают абсолютно жесткий брус AB и узел C. Поэтому, для определения неизвестных усилий сначала рассекаем систему сечением 1-1 по стержню BC и рассматриваем равновесие нижней части (рис. 2.32, б), а затем рассматриваем равновесие узла C (рис. 2.32, а).

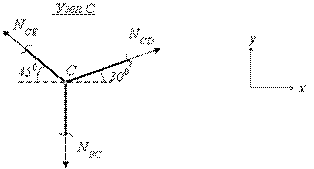
                                     Рис.2.32

 

Для определения усилия   необходимо записать уравнение моментов относительно точки  (рис. 2.32, б):

,

отсюда кН  - усилие растяжения.

Теперь, считая усилие   известным, необходимо рассмотреть равновесие узла С, для чего записать уравнения сумм проекций всех сил на вертикальную и горизонтальную оси (рис. 2.32, а):

,

.

В результате получаем систему двух уравнений с двумя неизвестными:

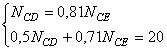
Решая систему определяем усилия в стержнях  и :

.

 

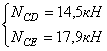Пример 16.

Два стальных (Е = 2·10⁵ МПа) стержня, шарнирно соединенные в точке А, находятся под действием силы Р (рис. 2.33). Первый стержень имеет длину с и площадь поперечного сечения F, второй длину а и площадь - 2F.

1) Найти величины нормальных напряжений, действующих в стержнях.

2) Найти абсолютную и относительную деформации стержней.

Дано: Р = 130 кН, с = 1,5 м, а = 2 м, F = 12 см.

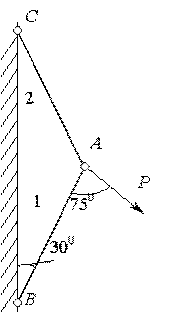
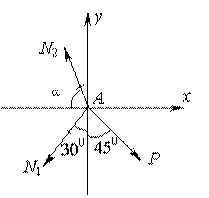
        Рис.2.33                                                       Рис.2.34

 

Решение.

Стержни прикреплены к стене и соединены между собой шарнирами (точках В, С и А). Шарниры предполагаются идеальными, т. е. такими, трение в которых отсутствует. Нагрузка Р приложена в узле А. Поэтому стержни будут испытывать только продольные (растягивающие или сжимающие) усилия, т.е. в поперечных сеченияхстержней возникает только один внутренний силовой фактор - продольная сила N.

1. Для определения усилий рассмотрим равновесие узла А (рис. 2.34), к которому приложены нагрузка Р и два неизвестных усилия N₁, и N₂, действующие со стороны стержней АВ и АС и направленные вдоль их осей.

При определении неизвестных усилий в стержнях обычно принято считать их растянутыми и соответственно этому направлять векторы сил от узла. Знак плюс в решении для усилия будет подтверждать правильность сделанного предположения о направлении усилия, а знак минус укажет на то, что в действительности усилие направлено противоположно и соответствующий стержень сжат.

Полагая оба стержня растянутыми, направим усилия N₁, и N₂ так, как показано на рис.2.34. Для плоской системы сил, пересекающихся в одной точке, как известно из курса теоретической механики, можно составить только два независимых уравнения равновесия - в виде сумм проекции всех сил на две оси, не параллельные друг другу.

В качестве таких осей выберем оси Х и Y (рис. 2.34). Тогда уравнения равновесия представятся в виде:

;

.                          (1)

Из этой системы (1) можно было бы определить неизвестные усилия N₁, и N₂,  если бы были известны значения  и . Определим эти величины. Для этого рассмотрим данную стержневую систему (рис. 2.34). Из точки А опустим перпендикуляр АD на прямую ВС, получим два прямоугольных треугольника  и .

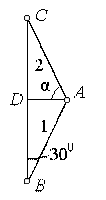
   Рис.2.35

 

Из треугольника ABD определим AD:

 м.

Из треугольника ADG получим:

.

Теперь определим неизвестные усилия N₁, и N₂ из системы двух линейных уравнений (1). Перепишем уравнения в следующем виде:

;

.                          

Решим эту систему используя метод Крамера

.

.

.

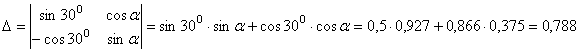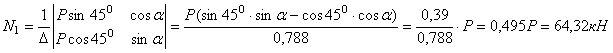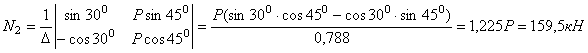2. Определим нормальные напряжения, действующие в стержнях.

Напряжения в стержнях определяются по формуле

.

Для первого стержня

,

для второго стержня

.

3. Найдем абсолютную и относительную деформации стержней.

Абсолютная деформация стержня длиной l равна:

.

Абсолютная деформация первого стержня

.

Абсолютная деформация второго стержня

.

Относительную деформацию определим из закона Гука

.

Относительная деформация первого стержня

,

Относительная деформация второго стержня

.

 

Понятие о статически неопределимых системах

Основные положения. Связи необходимые и дополнительные.

Для решения задач сопротивления материалов необходимо знать все внешние силы, действующие на конструкцию, включая реакции наложенных на нее связей. Из теоретической механики известно, что для равновесия твердого тела, нагруженного плоской системой сил, достаточно наложить на тело три связи, а нагруженного пространственной системой сил – шесть связей. Соответственно для таких систем можно составить три и шесть независимых уравнений равновесия. Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления можно определить с помощью уравнений равновесия, без использо­вания дополнительных условий, то такая система называется ста­тически определимой.

В реальной практике встречаются такие конструкции, при рас­чете которых одних лишь уравнений равновесия оказывается не­достаточно, в связи с чем требуется формулирование дополнитель­ных уравнений, связанных с условиями деформирования конструк­ции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

В машиностроении и строительных конструкциях такие системы на­ходят широкое применение. В одних случаях статическая неопределимость является сущностью самой конструкции.

                   

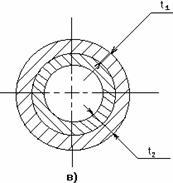
                                                                   Рис. 2.36

 

Примерами таких конструкций могут быть: армированные уголками стойки (рис.2.36, а); панель крыла самолета, состоящая из обшивки 1 с продольными ребрами 2 (рис. 2.36, б); составной цилиндр, полученный пу­тем напряженной посадки двух труб из различных материалов (рис. 2.36, в). В других случаях, с целью повышения жесткости и надежности сис­темы, вводятся дополнительные связи сверх тех минимально необходи­мых, которые обеспечивают ее кинематическую неизменяемость. Нало­жение на систему дополнительных связей превращает ее в статически неопределимую. Напомним, что кинематическая неизменяемость пло­ской системы обеспечивается тремя, а пространственной – шестью свя­зями.

Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. Лишними такие связи называются только потому, что они не являются необходимыми для обеспечения равновесия конст­рукции и ее геометрической неизменяемости, хотя постановка их дикту­ется условиями эксплуатации. По условиям прочности и жесткости кон­струкции лишние связи могут оказаться необходимыми.

В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.

                                                               

                                     а)                                                                    б)                                                    в) 

                                                                                            Рис. 2.37

 

На рис.2.37 приведены схемы 3-х плоских систем с «лишними» связями: а – стержневой подвески; б – стержня, закрепленного обоими концами; в – стержневого кронштейна. В схеме, показанной на рис. 2.37, в, вся система состоит из упругих звеньев. Подсчет числа наложенных связей произво­дится в этом случае следующим образом. Каждый стержень связан с опорной поверхностью двумя связями. Всего таких связей 8. Шарнир, соединяющий концы стержней, снимает связи, ограничивающие относи­тельный или взаимный их поворот. При соединении двух стержней од­ним шарниром снимается одна связь, трех стержней – две связи, четырех – три и т.д. В данном случае снимаются три связи. Следовательно, всех связей, наложенных на эту систему оказывается пять, две из которых мо­гут считаться «лишними».

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. За­ключаются они в том, что в элементах статически неопределимых систем напряжения возникают не только от действия внешних сил, но и в ре­зультате изменения температуры, неточности изготовления деталей, не­точностей их сборки, смещения мест опорных креплений и ряда других причин. Объясняется это тем, что деформация одного из элементов в статически неопределимой системе приводит к деформа­ции и других ее элементов.

Например, если один из стержней системы (рис. 2.37, в) изготовлен по длине неточно, то соединение концов стержней одним шарниром возможно только путем деформации всех стержней.

Сила, возникающая при деформации одного из стержней, вызывает усилия в других стержнях, находящихся с ним в шарнирном соединении. Смонтированная система приходит в равновесие, следовательно, сово­купность сил системы обеспечивает ее равновесие. Эти силы вызывают соответствующие, называемые начальными, напряжения в стержнях.

В статически неопределимых конструкциях при изменении темпера­туры ее элементов по сравнению с температурой, при которой осуществ­лялась сборка, возникают дополнительные усилия и напряжения, кото­рые принято называть температурными.

Распределение усилий между элементами системы зависит от их же­сткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живуче­стью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис. 2.37, в не приводит к потере способности восприни­мать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

 

Степень статической неопределимости. Методика ее определения.

Статически неопределимые системы характеризуются степенью ста­тической неопределимости, которая равна числу «лишних» связей и мо­жет быть вычислена как разность между числом неизвестных сил и чис­лом независимых уравнений равновесия. По числу единиц этой разности системы бывают 1,2,3….n раз статически неопределимыми.

Для расчетов составляется силовая схема заданной системы, на которой указываются все известные и неизвестные силовые факторы.

При составлении силовой схемы в случае определения внутренних силовых факторов применяется метод сечений, согласно которому каждое звено системы разделяется на две части в произвольном сечении, затем отбрасываются части, примыкающие к опорным элементам, а их действие на оставшиеся части заменяется продольными силами. После этого на схеме показываются все заданные внешние силы и реакции опор.

Затем по этой схеме устанавливается возможное число независимых уравнений равновесия. Степень статической неопределимости подсчитывается, как разность между числом неизвестных сил и числом независимых уравнений равновесия.

На рис.2.38, а изображен кронштейн, состоящий из двух стерж­ней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система яв­ляется плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла , т.е.

,     .                                                                                                                   (2.37)

Раскрывая эти уравнения, получаем замкнутую систему линей­ных уравнений относительно неизвестных усилий N₁ и N₂  в кото­рой количество уравнений равно количеству неизвестных:

;     .

Если конструкцию крон­штейна усложнить, добавив еще один стержень (рис.2.38, б), то усилия в стержнях N₁, N₂ и N₃ прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.37) имеются уже три неиз­вестных усилия в стержнях. В таких случаях говорят, что сис­тема один раз статически неопределима.

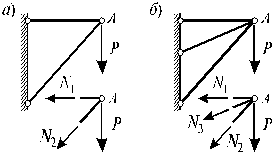
                                                     Рис.2.38

 

На рис.2.39 приведены примеры статически неопределимых систем. В стержне с жестко заделанными концами (рис.4.2, а) возникают две реакции, а уравнение равновесия можно составить только одно, следовательно, конструкция один раз статически неопределима. Не нарушая равновесия стержня, можно отбросить одну из опор. 

                                                                              Рис.2.39

 

Для системы из трех стержней (рис.2.39, б) можно составить два уравнения равновесия, а неизвестных сил в системе три, следовательно, система один раз статически неопределима. Один из стержней не нужен для равновесия системы, и его можно отбросить. Рассуждая аналогично, можно установить, что система из четырех стержней (рис.2.39, в) дважды статически неопределима.

Для определения внутренних сил в системе из пяти стержней (рис.2.39, г) необходимо вырезать и рассмотреть раздельно равновесие узлов  и . К каждому узлу примыкают три стержня (всего пять стержней и, следовательно, пять неизвестных сил), а уравнений равновесия для каждого узла можно составить два, т.е. всего четыре уравнения. Система один раз статически неопределима.

Напомним, что для пространственной системы сил можно составить шесть независимых уравнений равновесия: три уравнения, выражающие сумму проекций всех сил на три взаимно перпендикулярные оси (,, ), и три - сумму моментов всех сил относительно этих же осей (,,). Для общего случая сил, лежащих в одной плоскости- три независимых уравнения (например: ,,  ). В частных случаях плоской системы можно составить два независимых уравнения равновесия: для системы параллельных сил (например: ,) и для системы сил, линии действия которых пересекаются в одной точке (,). Для сил, линии действия которых лежат на одной прямой, можно записать только одно независимое уравнение (например: ).

На рис. 2.40 показаны примеры составления силовых схем и определения степени статической неопределимости по формуле

,

где n - общее число неизвестных сил, включая реакции опор; m - число возможных для данной системы независимых уравнений статики.

 

                  

           

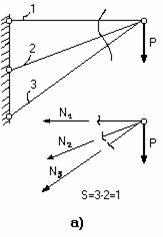
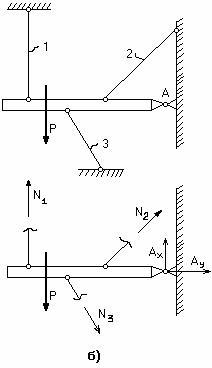
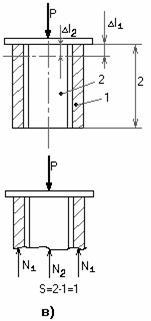
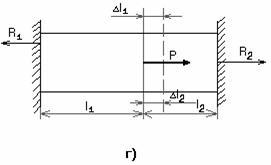
                                                      Рис.2.40

 

Раскрытие статической неопределимости

Операции по определению неизвестных силовых факторов в статически неопределимых системах принято называть раскрытием статической неопределимости. Производятся они следующим образом. В начале исходя из силовой схемы составляются уравнения равновесия. 

При решении любых задач число уравнений должно быть равно числу неизвестных. Для определения сил в стержнях статически неопределимых систем следует составлять уравнения, дополняющие уравнения равновесия до числа неизвестных сил. Дополнительные уравнения, называемые уравнениями совместности перемещений или деформаций, составляют, определяя перемещения отдельных стержней системы и устанавливая между ними связь.    

Принцип совместности деформирования выражает условие, заключающееся в том, что конструкция должна деформироваться без разъединения и непредусмотренного взаимного перемещения отдельных ее звеньев.

Для облегчения записей уравнений перемещений строят схему деформаций всех упругих элементов или схему деформированной системы. Для любой статистически неопределимой системы всегда можно составить столько дополнительных уравнений, сколько раз система статически неопределима.

В силу различной взаимозависимости элементов, различия накладываемых связей и условий деформирования, уравнения совместности деформаций систем записываются по разному. Но все они выражают соотношения деформаций (перемещений) отдельных упругих элементов системы. Например, на схеме,

на рис. 2.40, в     

а на рис. 2.40, г.    

т. к. весь стержень не может не удлиниться, ни укоротиться. На схеме (рис. 2.40, а) можно установить геометрическое соотношение деформаций стержней 1, 2 и 3.

После получения указанных геометрических соотношений величины абсолютных изменений, длины стержней  заменяют по закону Гука их выражениями через усилия :

Полученные таким образом уравнения, содержащие в качестве неизвестных продольные силы, и являются дополнительными уравнениями. Они включают также показатели жесткости отдельных звеньев конструкции, вводя тем самым зависимость распределения сил внутри системы от жесткости ее элементов. Вместе с уравнениями статистики общее число уравнений равно числу неизвестных сил. Решая их, определяют неизвестные внутренние (продольные) силы.

В заключение может быть выполнена энергетическая проверка решения задачи. Она заключается в составлении и удовлетворении равенства работы внешних сил А и суммы потенциальной энергии деформации элементов системы U.

Сложные статически неопределимые системы, в том числе статически неопределимые фермы (элементы ферм работают на растяжение, сжатие) и статически неопределимые рамы, рассматриваются в курсе строительной механики стержневых систем. В курсе сопротивления материалов рассматриваются обычно простейшие статически неопределимые системы, к которым относятся:

а) прямые стержни постоянного, кусочно-постоянного и переменного сечений, закрепленные с двух сторон, от нагрузки действующей вдоль оси стержня;

б) системы шарнирно соединяемых стержней с возможным включением жестких недеформируемых элементов.

При решении статически неопределимых систем, в стержнях которых действуют продольные силы, можно отметить основные этапы:

1) анализ работы конструкции с указанием действующих силовых факторов и выяснением деформации ее элементов, определение степени статической неопределимости;

2) статическая сторона задачи – составляют уравнения равновесия для системы или отсеченных ее частей;

3) геометрическая сторона задачи – выясняют, как деформируются стержни системы, изображают систему в деформированном виде, устанавливают связи между перемещениями отдельных элементов системы, составляют уравнения совместности перемещений;

4) физическая сторона задачи – выражает деформации элементов, согласно закону Гука, через действующие в них неизвестные усилия;

5) синтез – определяют неизвестные силы, решая совместно систему уравнений равновесия и перемещений.

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. Так, при эксплуатации конструкции возможно изменение ее температуры, вызванное условиями работы или сменой времен года. С изменением температуры изменяются линейные размеры элементов конструкции: увеличиваются при нагреве, уменьшаются при охлаждении на величину

,                                                                                                                           (2.38)

где - температурный коэффициент линейного расширения (см. раздел «Справочные данные»);  - длина элемента; - изменение температуры, (⁰С).

В статически определимых системах длина стержня может свободно изменяться при их нагреве или охлаждении (рис.2.41, а, б).

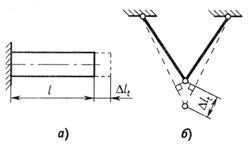
                                             Рис.2.41

 

В статически неопределимых системах при изменении температуры возникают дополнительные силы. Если нагреть стержень, жестко закрепленный по концам (рис.2.42, а), то его длина не может изменяться: этому препятствуют жесткие заделки. В опорах (заделках) возникают реакции, сжимающие стержень.

Так как неизвестных сил две, а уравнение равновесия можно составить только одно: , то система один раз статически неопределима.

Решая геометрическую часть задачи, составляем уравнение перемещений. Отбросим одну из опор и заменим ее действие неизвестной силой . Теперь стержень при нагреве может удлиниться на величину  (рис.2.42, б).

                                        Рис.2.42

 

Так как длина стержня остается неизменной, перемещение сечения  должно быть равно нулю, следовательно, сила должна сжать стержень на величину, равную его удлинению при нагреве:

.

Решая физическую часть задачи, с учетом равенства  получаем

.

Тогда продольная сила в сечениях стержня

;

напряжение в стержне

.

Отметим, что напряжение в стержне не зависит от площади сечения.

Элементы конструкций изготовляют с определенной точностью. При сборке статически неопределимых систем, имеющих неточно изготовленные стержни, стержни приходится деформировать (удлинять или укорачивать), при этом в них возникают напряжения, называемыми начальными или монтажными.

Рассмотрим систему, один из стержней которой изготовлен короче, чем требуется, на величину  (рис.2.43, а). Определим внутренние силы и напряжения, возникающие в стержнях системы при ее сборке. Стержни имеют одинаковые размеры и изготовлены из одного материала.

                                                   Рис.2.43

 

При сборке системы все три стержня необходимо удлинить, приложив к ним растягивающие силы. В собранном виде система показана штриховыми линиями (см. рис.2.43, а). Вырежем узел  (рис.2.43, б), составим уравнения равновесия сил

,

откуда

;

.

Система один раз статически неопределима. Рассмотрим геометрическую часть задач и составим уравнение перемещений. Из схемы, представленной на рис.2.43, а, следует, что

, где .

Уравнение перемещений принимает вид

.

Используя закон Гука, выразим удлинение через неизвестные силы в стержнях

.

Решив уравнение перемещений совместно с уравнениями равновесия, получим

;       .

Начальные напряжения часто специально создают в статически неопределимых системах, таких, например, как соединения с натягом и резьбовые соединения. Создавая в элементах статически неопределимой системы начальные напряжения, знак которых противоположен знаку напряжения от внешних сил, можно повысить прочность конструкции или увеличить допускаемую для нее нагрузку.

Распределение усилий между элементами системы зависит от их же­сткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живуче­стью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис.2.39, в не приводит к потере способности восприни­мать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

В заключение отметим следующие основные свойства статически неопреде­лимых систем.

1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически опре­делимой системой оказывается более жесткой, а при идентичном характере нагружения значения усилий получаются меньшими. Следовательно, и более экономичными.

2. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.

3. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.

4. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.

5. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Решение статически неопределимых систем можно вести, используя три метода:

- расчет по упругой стадии деформации (допускаемым напряжениям);

- расчет по разрушающим нагрузкам;

- расчет по предельному пластическому состоянию.

В машиностроении отдается предпочтение первому методу, а в строительстве – второму и третьему.

Если в качестве физических уравнений используется закон Гука, то такой способ расчета носит название расчета по упругой стадии деформаций. После определения внутренних усилий – продольных сил в стержнях статически неопределимой системы – встает задача обеспечения ее прочности. При расчете по упругой стадии деформаций считается, что предельное состояние конструкции наступает тогда, когда один, наиболее напряженный, стержень переходит в предельное состояние (разрушится или потечет). Поэтому после определения усилий по этому способу находим напряжения в стержнях и выбираем стержень, в котором действует максимальное напряжение. Из условия прочности этого наиболее напряженного стержня либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней. Следует отметить, что в большинстве статически неопределимых конструкций в результате расчета по этому способу только в одном стержне напряжения будут равны допускаемым, остальные же стержни будут недогружены. Достичь равенства напряжений во всех элементах конструкции и, следовательно, добиться выполнения требования, чтобы напряжения во всех стержнях равнялись допускаемым, в общем случае невозможно.

Второй способ расчета статически неопределимых стержневых систем носит название расчета по предельному пластическому состоянию. Благодаря наличию лишних стержней в статически неопределимой системе, наступление состояния текучести в одном (наиболее напряженном) стержне еще не приводит к нарушению геометрической неизменяемости  всей конструкции. Остальные стержни, оставаясь упругими, препятствуют пластическим деформациям этого стержня. Конструкция продолжает выполнять свое назначение, перейдя из упругой стадии работы в упругопластическую. При увеличении  нагрузки в пластическую стадию работы вовлекаются все новые стержни. И только тогда, когда в системе потекут все лишние стержни и хотя бы один необходимый, конструкция превращается в механизм и не может выполнять свои функции. Это состояние и считается предельным при расчете по предельному пластическому состоянию. Таким образом, расчет по предельному пластическому состоянию сводится к следующему:

1) определяем, сколько стержней должно потечь, чтобы конструкция превратилась в механизм. Дальнейший расчет возможен по двум вариантам:

- если в предельном состоянии текут все стержни системы, то, составляя уравнения равновесия конструкции в предельном состоянии, находим из него значение предельной нагрузки ;

- если в предельном состоянии течет только часть стержней, то, не определяя порядка перехода стержней в пластическое состояние, рассматриваем все кинематически возможные варианты предельного состояния конструкции. Находим из уравнений равновесия предельную нагрузку для каждого варианта. Выбираем из всех вариантов минимальное значение предельной нагрузки ;

2) из условия прочности конструкции по предельному состоянию  либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней.

Отметим, что расчет по предельному пластическому состоянию является более экономичным, чем расчет по упругой стадии деформаций. Поэтому при сравнении результатов расчета по двум способам должно получиться, что допускаемая нагрузка, найденная расчетом по предельному пластическому состоянию, всегда не меньше нагрузки, полученной расчетом по упругой стадии деформации. Соответственно площади сечений стержней, найденные расчетом по предельному состоянию, должны быть не больше площадей сечений, полученных расчетом по упругой стадии деформаций.

    

Примеры типовых расчетов статически неопределимых систем

Рассмотрим основные этапы расчета статически неопределимых систем на примере простейших конструкций.

Пример 17.

Определить продольные силы в сечениях ступенчатого стержня, жестко закрепленного по концам (рис.2.44, а).

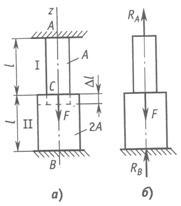
                                    Рис.2.44

 

Решение.

Под действием силы  в заделках возникают опорные реакции  и . Единственное уравнение равновесия имеет вид

,

следовательно, система один раз статически неопределима. Для раскрытия статической неопределимости отбросим одну из опор, например верхнюю (рис.2.44, б), и составим для стержня уравнение совместности перемещений. Так как длина стержня не изменяется (он жестко закреплен по концам), удлинение верхней части стержня должно быть равно укорочению нижней, т.е. перемещение сечения 

.

Уравнение совместности перемещений можно записать в ином виде, определив перемещение верхнего сечения под действием сил  и . Так как это сечение закреплено, его перемещение равно нулю

.

Очевидно, оба уравнения совместности перемещений равнозначны.

На основании закона Гука, уравнение совместности перемещений запишем в виде

.

Решив совместно уравнение равновесия и уравнение перемещений, получим

;      .

Используя метод сечений, находим

;      .

Отметим, что в более жесткой нижней части стержня возникает бóльшая по абсолютному значению продольная сила. 

 

Пример 18.

К стержню, закрепленному обоими концами, приложена осевая сила Р (рис.2.45). Определить опорные реакции R₁ и R₂, если известны l₁, l₂ и Р.

Решение.