2. Геометрическая сторона задачи.

При повороте гайки на угол  стержень 3, состоящий из двух частей, ввинтится в гайку на величину  

             Рис. 2.51

 

За счет ввинчивания стержня 3 точки А и В сблизятся на величину , а за счет растяжения этого стержня и стяжки они разойдутся на величину  (рис. 2.51). Тогда, на основании схемы деформированной системы, ус­ловие совместности деформаций будет иметь вид:

                                 (с) 

3. Физическая сторона задачи.

Согласно закону Гука.

  ;     ;             (d)

Здесь l₁=l₂ по условию, а l₂ и l₃ можно определить из равенства проекций стержней на горизонтальную и вертикальную оси (рис. 2.50, а):

               

Подставляя (d) в (с), получим:

           (е)

4. Определение неизвестных.

Решая систему, составленную из уравнений (а), (в) и (е), получим:

 

Пример 24.

Определить усилия в стержнях системы, возникающие в результате повышения температуры всех стержней на  (рис. 2.52, а)

Дано: F₁=F₂=F;           E₁=0,5E;             E₂=E;       ;       ;          l₁=l 

                            Рис.2.52

 

Решение.

1. Статическая сторона задачи.

С учетом симметрии относительно оси Y имеем:

,

отсюда                                                      (a)

2. Геометрическая сторона задачи.

В результате термического расширения точка А переместится в А₁ (рис. 2.52, б). Исходя из схемы деформированной конструкции можно составить условие совместности деформаций:

                                                                        (b)

3. Физическая сторона задачи.

Крайние стержни 1 длиннее среднего стержня 2; кроме того, у край­них стержней коэффициент линейного расширения больше, чем у сред­него. По этой причине точка А у первых стержней опустилась бы ниже, чем точка А у второго стержня, если бы они деформировались отдельно. Но так как они в точке А связаны шарниром, то возникает силовое взаи­модействие боковых и среднего стержней. Боковые стержни, удлиняясь за счет термического воздействия, будут одновременно укорачиваться в результате действия возникающего усилия, средний же стержень будет удлиняться как за счет термического расширения, так и за счет механи­ческого действия на него крайних стержней.

Следовательно

            (c)

где 

подставляя (с) в (б), получим:

                           (d)

4. Определение неизвестных.

Решая систему уравнений (а) и (d) с учетом, что R₁=N₁ и R₂=N₂, получим:

 

Пример 25.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 2.53). Исходные данные: а = 2,1 м, b= 2,4 м, с = 1,5 м, F = 12см², Е = 2·10⁵ МПа.

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу Q;

2. допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению  = 160 МПа;

3. предельную грузоподъемность системы Q_пр. и допускаемую нагрузку [Q_пр], если предел текучести = 240 МПа и запас прочности n = 1,5;

4. сравнить величины допускаемых нагрузок [Q] и [Q_пр].

                                                     Рис.2.53

 

Решение.

Усилия N₁, и N₂ в стержнях АА₁, и ВВ₁, шарнирно прикрепленных по концам, направлены вдоль осей этих стержней. Реакция опоры К имеет горизонтальную составляющую Н_К, и вертикальную составляющую R_К, т.к. эта опора препятствует горизонтальному и вертикальному перемещению точки К бруса.

Таким образом, всего имеется четыре неизвестные реакции (рис.2.54), а уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима. Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи.

                                              Рис. 2.54

 

1. Найдем усилия и напряжения в стержнях, выразив их через силу Q.

Статическая сторона задачи. По условию задачи необходимо определить усилия N₁, и N₂ стальных стержней АА₁, и ВВ₁, a в определений реакций Н_К, и R_К нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакция Н_К, и R_К . Таким является уравнение в виде суммы моментов всех сил относительно шарнира К:

,

где м.

Подставляя в уравнение значения h, b, с, получим

.                                  (а)

 

                                             Рис.2.55

 

                Геометрическая сторона задачи. Под действием внешней силы Q абсолютно жесткий брус повернется вокруг точки К. Шарниры А и В после деформации переходят в положение А₂ и В₂ соответственно, т.е. перемещаются по вертикали на величины  и  (рис.2.55).

Из подобия треугольников AA₂К и ВВ₂К находим

.                                                           (b)

Выразим укорочение стержня АА₁ и удлинение   стержня ВB₁, через перемещения  и .

,             ,

откуда

или с учетом равенства (b)

                                     (c)

Физическая сторона задачи. Используя закон Гука, записанный для абсолютных деформаций, выразим удлинения стержней через усилия

;

;                                  (d)

Подставим выражения (c) в условие (d)

,

после сокращения получим

                                                         (e)

Решаем совместно уравнения статики (a) и уравнение (e):

.

Определяем напряжения в стержнях 1 и 2:

Па,

Па.

2. Найдем допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению  = 160 МПа.

,

откуда

Н.

3. Найдем предельную грузоподъемность системы Q_пр. и допускаемую нагрузку [Q_пр], если предел текучести = 240 МПа и запас прочности  n = 1,5.

При увеличении нагрузки Q cверх значения [Q] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величины  напряжение  во второй стержне достигают предела текучести , а усилие N₂ - предельного значения N_2пр = c₁·F. При этом напряжение в первом стержне остается меньше . В процессе дальнейшего увеличения нагрузки напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом - возрастают, пока также не становятся равными , усилие N₁ при этом равно . Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. ВеличинуQ, вызываюшую предельное состояние, обозначают Q_пр и называют предельной нагрузкой.

Для определения Q_пр, подставим в уравнение (a) значения сил, соответствующих предельному состоянию, когда Q = Q_пр, N₁ = N_1пр, N₂ =  N_2пр:

,

откуда

Н.

Н.

4. Сравним величины допускаемых нагрузок [Q] и [Q_пр]

.

Следовательно, при расчете на прочность данной системы по предельной нагрузке грузоподъемность ее увеличивается на 38%.

 

Расчет конструкций по допускаемым нагрузкам.

Расчет статически определимых систем по способу допускаемых нагрузок.

   В предыдущем изложении методов расчета мы исходили из основного условия прочности . Это неравенство требует выбора размеров конструкции с таким расчетом, чтобы наибольшее напряжение в самом опасном месте не превосходило допускаемого.

   Но можно стать на другую точку зрения. Можно задать условие, чтобы действительная нагрузка на всю конструкцию не превосходила некоторой допускаемой величины. Условие это можно выразить таким неравенством:

   

За допускаемую нагрузку надо выбрать некоторую  часть той нагрузки, при которой конструкция перестанет функционировать правильно, перестанет выполнять свое назначение. Такая нагрузка обычно называется предельной, иногда—разрушающей в широком смысле слова (под разрушением конструкции подразумевают прекращение ее нормальной работы).

В качестве примера возьмем систему из двух стальных стержней АВ и АС  (рис.2.56), нагруженных силой P.

 

                                 Рис.2.56

 

 Рассчитывая эту систему обычным путем, найдем усилия N₁ = N₂ no формуле:

(из равновесия узла А). Отсюда площадь каждого из стержней равна:

По способу допускаемых нагрузок имеем:

Введя в качестве коэффициента запаса для конструкции в целом ту же величину k, которая была принята в качестве коэффициента запаса для напряжений, мы получим, что величина 

Предельной, опасной величиной P_пр будет та, при которой напряжения в стержнях дойдут до предела текучести:

Таким образом, допускаемая величина Р равна:

Условие прочности принимает вид

а учитывая, что

,

получаем:

Отсюда:

Таким образом, расчет по допускаемым нагрузкам привел в данном случае к тем же результатам, что и расчет по допускаемым напряжениям. Это всегда имеет место для статически определимых конструкций при равномерном распределении напряжений, когда материал по всему сечению используется полностью.

 

Расчет статически неопределимых систем по способу допускаемых нагрузок

Совсем другие результаты мы получим, если будем применять способ допускаемых нагрузок к статически неопределимым системам, стержни которых изготовлены из материала, обладающего способностью к большим пластическим деформациям, например из малоуглеродистой стали.

В качестве примера рассмотрим систему из трех стержней, нагруженных силой Q (рис. 2.57). Пусть все стержни сделаны из малоуглеродистой стали с пределом текучести . Длины крайних стержней, как и выше, обозначим ; длину среднего . Допускаемое напряжение .

 

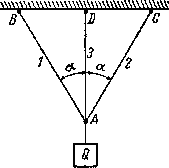                                    Рис.2.57

 

Как и раньше, при расчете этой статически неопределимой системы зададимся отношением площадей стержней; примем, что все три стержня будут иметь одинаковую площадь F. Получим:

1. 

2. 

3. .

Используя закон Гука, получим:

Следовательно:

Так как , средний стержень напряжен больше, чем крайние; поэтому подбор площади сечения F надо произвести по формуле:

Ту же величину площади надо дать и боковым стержням; в них получается некоторый дополнительный запас.

Применим способ допускаемых нагрузок; условием прочности будет:

Что в данном случае следует понимать под предельной нагрузкой конструкции? Так как конструкция выполнена из материала, имеющего площадку текучести, то, по аналогии с простым растяжением стержня из такого материала, за предельную нагрузку следует взять груз, соответствующий достижению состояния текучести для всей конструкции в целом. Назовем эту нагрузку . Пока сила Q не достигла этого значения, для дальнейшей деформации (опускания точки A) требуется возрастание нагрузки. Когда же Q сделается равным , дальнейший рост деформаций будет происходить уже без увеличения нагрузки, — конструкция выйдет из строя.

Для определения величины рассмотрим постепенный ход деформации нашей стержневой системы. Так как средний стержень напряжен сильнее крайних, то в нем раньше, чем в других, напряжение дойдет до предела текучести. Нагрузку, соответствующую этому моменту, обозначим Q_Т; она будет равна:

где — усилие в среднем стержне, соответствующее его пределу текучести.

Напряжения в крайних стержнях, имеющих ту же площадь, в этот момент еще не дойдут до предела текучести, и эти стержни будут упруго сопротивляться дальнейшей деформации. Для того чтобы эта деформация происходила, необходимо дальнейшее увеличение нагрузки до тех пор, пока в крайних стержнях напряжения тоже не дойдут до предела текучести. Лишь тогда будет достигнута предельная грузоподъемность конструкции .

Так как при нагрузке Q_Т напряжения в среднем стержне дойдут уже до предела текучести , то при дальнейшем возрастании груза они, а стало быть и усилие N₃, останутся без увеличения. Наша статически неопределимая система превратится в статически определимую, состоящую из двух стержней АВ и АС и нагруженную в точке Асилой Q, направленной вниз, и известным усилием , равным  (рис.2.58).

 

                                     Рис.2.58

 

Такая схема работы нашей конструкции будет иметь место, пока

Для иллюстрации хода деформации рассматриваемой конструкции изобразим графически зависимость между силой Q и перемещением f точки А (рис. 2.59). Пока опускание точки А равно удлинению среднего стержня и определяется формулой

.

 

                                     Рис.2.59

 

Как только Q будет заключаться в промежутке перемещение точки А должно быть вычислено, как опускание этого узла в системе двух стержней АС иАВ, нагруженных в точке А силой . Так как:

и, в свою очередь:

;

Отсюда

; 

Для f₁₂ (на втором участке) получаем уравнение прямой, но уже не проходящей через начало координат. После достижения нагрузкой Q значения напряжения в крайних стержнях достигнут предела текучести, и система будет деформироваться без увеличения нагрузки. График перемещения идет теперь параллельно оси абсцисс.

Для определения предельной грузоподъемности всей системы мы должны для системы двух стержней, нагруженных силой , найти то значение Q, при котором напряжения и в крайних стержнях дойдут до предела текучести. Такая задача решена в предыдущем параграфе; подставляя в выражение (а) вместо Р величину , получаем:

Отсюда

Допускаемая нагрузка будет равна

а учитывая, что

,

получаем

Окончательно:

и

Эта величина меньше, чем полученная обычным методом расчета, т. е.

При  (сталь) получаем: по обычному способу

по способу допускаемых нагрузок:

Таким образом, метод расчета по допускаемым нагрузкам позволяет спроектировать статически неопределимую систему из материала, обладающего площадкой текучести, экономичнее, чем при расчете по допускаемым, напряжениям. Это понятно: при способе расчета по допускаемым напряжениям мы считали за предельную нагрузку нашей конструкции величину Q_Т, при которой до предела текучести доходил лишь материал среднего стержня, крайние же были недонапряжены. При методе расчета по допускаемым нагрузкам предельная грузоподъемность определяется величиной . При нагрузке полностью используется материал всех трех стержней.

Таким образом, новый метод расчета позволяет реализовать скрытые при старом способе запасы прочности в статически неопределимых системах, добиться повышения их расчетной грузоподъемности и действительной равнопрочности всех частей конструкции. Не представит никаких затруднений распространить этот метод на случай, когда соотношение площадей среднего и крайних стержней не будет равно единице.

Изложенные выше теоретические соображения проверялись неоднократно на опыте, причем всегда наблюдалась достаточно близкая сходимость величин предельной нагрузки — вычисленной и определенной при эксперименте. Это дает уверенность в правильности теоретических предпосылок метода допускаемых нагрузок.

 

Расчет гибких нитей

В технике встречается еще один вид растянутых элементов, при определении прочности которых важное значение имеет собственный вес. Это — так называемые гибкие нити. Таким термином обозначаются гибкие элементы в линиях электропередач, в канатных дорогах, в висячих мостах и других сооружениях.

Пусть (рис.2.60) имеется гибкая нить постоянного сечения, нагруженная собственным весом и подвешенная в двух точках, находящихся на разных уровнях. Под действием собственного веса нить провисает по некоторой кривой АОВ.

Горизонтальная проекция расстояния между опорами (точками ее закрепления), обозначаемая , носит название пролета.

Нить имеет постоянное сечение, следовательно, вес ее распределен равномерно по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, и длина кривой АОВ мало отличается (не более чем на 10%) от длины хорды АВ. В этом случае с достаточной степенью точности можно считать, что вес нити равномерно распределен не по ее длине, а по длине ее проекции на горизонтальную ось, т. е. вдоль пролета l.

 

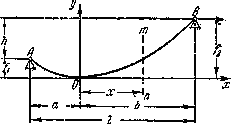                                            Рис.2.60

 

Эту категорию гибких нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равномерно распределенной по пролету нити, равна q. Эта нагрузка, имеющая размерность сила/длина, может быть не только собственным весом нити, приходящимся на единицу длины пролета, но и весом льда или любой другой нагрузкой, также равномерно распределенной. Сделанное допущение о законе распределения нагрузки значительно облегчает расчет, но делает его вместе с тем приближенным; если при точном решении (нагрузка распределена вдоль кривой) кривой провисания будет цепная линия, то в приближенном решении кривая провисания оказывается квадратной параболой.

Начало координат выберем в самой низшей точке провисания нити О, положение которой, нам пока неизвестное, очевидно, зависит от величины нагрузки q, от соотношения между длиной нити по кривой и длиной пролета, а также от относительного положения опорных точек. В точке О касательная к кривой провисания нити, очевидно, горизонтальна. По этой касательной направим вправо ось .

Вырежем двумя сечениями — в начале координат и на расстоянии от начала координат (сечение m — n) — часть длины нити. Так как нить предположена гибкой, т. е. способной сопротивляться лишь растяжению, то действие отброшенной части на оставшуюся возможно только в виде силы, направленной по касательной к кривой провисания нити в месте разреза; иное направление этой силы невозможно.

   На рис.2.61 представлена вырезанная часть нити с действующими на нее силами. Равномерно распределенная нагрузка интенсивностью q направлена вертикально вниз. Воздействие левой отброшенной части (горизонтальная сила Н) направлено, ввиду того, что нить работает на растяжение, влево. Действие правой отброшенной части, сила Т, направлено вправо по касательной к кривой провисания нити в этой точке.

Cоставим уравнение равновесия вырезанного участка нити. Возьмем сумму моментов всех сил относительно точки приложения силы Т и приравняем ее нулю. При этом учтем, опираясь на приведенное в начале допущение, что равнодействующая распределенной нагрузки интенсивностью q будет , и что она приложена посредине отрезка . Тогда

                                         Рис.2.61

 

 ,

откуда

                                                                                           (2.39)

Отсюда следует, что кривая провисания нити является параболой. Когда обе точки подвеса нити находятся на одном уровне, то . Величина в данном случае будет так называемой стрелой провисания. Ее легко определить. Так как в этом случае, ввиду симметрии, низшая точка нити находится посредине пролета, то ; подставляя в уравнение (2.39) значения  и  получаем:

                                                                                                (2.40)

Из этой формулы находим величину силы Н:

                                                                                                (2.41)

Величина Н называется горизонтальным натяжением нити.

Таким образом, если известны нагрузка q и натяжение H, то по формуле (2.40) найдем стрелу провисания . При заданных и натяжение Н определяется формулой (2.41). Связь этих величин с длиной  нити по кривой провисания устанавливается при помощи известной из математики приближенной формулы)

Составим еще одно условие равновесия вырезанной части нити, а именно, приравняем нулю сумму проекций всех сил на ось :

Из этого уравнения найдем силу Т — натяжение в произвольной точке

Откуда следует, что сила Т увеличивается от низшей точки нити к опорам и будет наибольшей в точках подвеса — там, где касательная к кривой провисания нити составляет наибольший угол с горизонталью. При малом провисании нити этот угол не достигает больших значений, поэтому с достаточной для практики степенью точности можно считать, что усилие в нити постоянно и равно ее натяжению Н. На эту величину обычно и ведется расчет прочности нити. Если все же требуется вести расчет на наибольшую силу у точек подвеса, то для симметричной нити ее величину определим следующим путем. Вертикальные составляющие реакций опор равны между собой и равны половине суммарной нагрузки на нить, т. е. . Горизонтальные составляющие равны силе Н, определяемой по формуле (2.41). Полные реакции опор получатся как геометрические суммы этих составляющих:

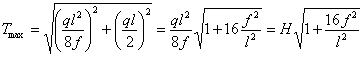
Условие прочности для гибкой нити, если через F обозначена площадь сечения, имеет вид:

Заменив натяжение Н его значением по формуле (2.41), получим:

   Из этой формулы при заданных , , и  можно определить необходимую стрелу провисания . Решение при этом упростится, если в включен лишь собственный вес; тогда , где — вес единицы объема материала нити, и

т. е. величина F не войдет в расчет.

Если точки подвеса нити находятся на разных уровнях, то, подставляя в уравнение (2.39) значения  и , находим  и :

Отсюда из второго выражения определяем натяжение

а деля первое на второе, находим:

или 

Имея в виду, что , получаем:

или  

Подставив это значение  в формулу определенного натяжения Н, окончательно определяем:

                                                                                    (2.42)

Два знака в знаменателе указывают на то, что могут быть две основные формы провисания нити. Первая форма при меньшем значении Н (знак плюс перед вторым корнем) дает нам вершину параболы между опорами нити. При большем натяжении Н (знак минус перед вторым корнем) вершина параболы расположится левее опоры А. Получаем вторую форму кривой. Возможна и третья (промежуточная между двумя основными) форма провисания, соответствующая условию ; тогда начало координат совмещается с точкой А. Та или иная форма будет получена в зависимости от соотношений между длиной нити по кривой провисания АОВ (рис.2.60) и длиной хорды АВ.

Если при подвеске нити на разных уровнях неизвестны стрелы провисания  и , но известно натяжение Н, то легко получить значения расстояний а и b и стрел провисания  и . Разность h уровней подвески равна:

Подставим в это выражение значения  и , и преобразуем его, имея в виду, что :

откуда

а так как  то

и 

 Следует иметь в виду, что при   будет иметь место первая форма провисания нити, при  — вторая форма провисания и при  — третья форма. Подставляя значения  и  в выражения для стрел провисания  и , получаем величины  и :

Теперь выясним, что произойдет с симметричной нитью, перекрывающей пролет , если после подвешивания ее при температуре  и интенсивности нагрузки температура нити повысится до а нагрузка увеличится до интенсивности  (например, из-за ее обледенения). При этом предположим, что в первом состоянии задано или натяжение , или стрела провисания  (Зная одну из этих двух величин, всегда можно определить другую.)

При подсчете деформации нити, являющейся по сравнению с длиной нити малой величиной, сделаем два допущения: длина нити равна ее пролету, а натяжение постоянно и равно Н. При пологих нитях эти допущения дают небольшую погрешность.

В таком случае удлинение нити, вызванное увеличением температуры, будет равно

где — коэффициент линейного температурного расширения материала нити.

При повышении температуры нить удлиняется. В связи с этим увеличится ее стрела провисания и, как следствие, уменьшится ее натяжение. С другой стороны, из-за увеличения нагрузки, как видно из формулы (2.41), натяжение увеличится. Допустим, что окончательно натяжение увеличивается. Тогда удлинение нити, вызванное увеличением натяжения, будет, согласно закону Гука, равно:

Если  окажется меньше, чем то величина будет отрицательной. При понижении температуры будет отрицательной величина.

   Таким образом, длина нити во втором ее состоянии будет равна длине при первом ее состоянии с добавлением тех деформаций, которые произойдут от повышения температуры и натяжения:

Изменение длины нити вызовет изменение и ее стрелы провисания. Вместо , она станет .

Теперь заменим в последнем уравнении и  их известными выражениями, а деформации и — также их полученными ранее значениями. Тогда уравнение для S₂ примет следующий вид:

В этом уравнении заменим  и их значениями по формуле (2.40):

и 

Тогда, после некоторых преобразований, уравнение для расчета натяжения может быть написано в виде:

Определив из этого уравнения натяжение , можно найти по формуле (2.40) и стрелу .

В случае, если при переходе от первого ко второму состоянию нагрузка не изменяется, а изменяется лишь температура, то в последнем уравнении интенсивность заменяется на . В случае, если при переходе от первого ко второму состоянию не изменяется температура, а изменяется лишь нагрузка, то в этом уравнении средний член в квадратной скобке равен нулю. Полученное уравнение пригодно, конечно, и при понижении температуры и уменьшении нагрузки.

В тех случаях, когда стрела провисания не является малой по сравнению с пролетом, выведенные выше формулы, строго говоря, неприменимы, так как действительная кривая провисания нити, цепная линия, будет уже значительно отличаться от параболы, полученной нами благодаря предположению о равномерном распределении нагрузки по пролету нити, а не по ее длине, как то имеет место в действительности.

Точные подсчеты показывают, что значение погрешности в величине натяжения Н, вызванной этим предположением, таково: при отношении   погрешность не превосходит 0,3%, при  ошибка составляет уже 1,3%, а при   погрешность несколько, превосходит 5%.

 

Лекция 2 (продолжение). Примеры решения на осевое растяжение – сжатие и задачи для самостоятельного решения

 

Расчет статически определимых стержней на растяжение-сжатие

Пример 1.

Круглая колонна диаметра d сжимается силой F. Определить увеличение диаметра , зная модуль упругости Е и коэффициент Пуассона  материала колонны.

Р е ш е н и е.

Продольная деформация по закону Гука равна  

.

Используя закон Пуассона, находим поперечную деформацию  

.

С другой стороны, .

Следовательно,  .

 

Пример 2.

Построить эпюры продольной силы, напряжения и перемещения для ступенчатого бруса.

Р е ш е н и е.

1. Определение опорной реакции. Составляем уравнение равновесия в проекции  на ось z: 

,   ,

откуда   R_E = 2qa.

2. Построение эпюр   N_z, , W.

Э п ю р а   N_z. Она строится по формуле  

.

Имеем     

,     

,    

.

Э п ю р а  . Напряжение равно . Как следует из этой формулы, скачки на эпюре  будут обусловлены не только скачками N_z, но также резкими изменениями площади поперечных сечений. Определяем значения  в характерных точках:

и строим эпюру .

Э п ю р а   W. Она строится по формуле

.

Построение ведем от защемления к свободному концу. Находим перемещения в характерных сечениях:

W_o = W_E = 0,

и строим эпюру W.

 

Пример 3.

Для стержня, изображенного на рисунке, построить эпюру нормальной силы и определить удлинение стержня, если F₁ = 100 кН, F₂ = 50 кН, q = 40 кН/м, а = 1 м, b = 2 м, с = 1,5 м, Е = 210⁵ МПа, S = 0,2 м².

Решение.

1. Разбиваем брус на участки АВ, ВС, CD

2. Определяем значение нормальной силы на каждом участке

     

CD         

CB         

при z₂=1,5 м, N₂=-100 кН,

при z₂=3,5 м, N₂=-20 кН,

BА         

кН

1) Строим эпюру нормальной силы

2) Определяем удлинение стержня

 

Пример 4. 

Построить эпюру  для колонны переменного сечения (рис. а). Длины участков 2 м. Нагрузки: сосредоточенные =40 кН, =60 кН, =50 кН; распределенная =20 кН/м.

 

Решение:

Пользуемся методом сечений. Рассматриваем (поочередно) равновесие отсеченной (верхней) части колонны (рис. в).

Из уравнения  для отсеченной части стержня в произвольном сечении участка  продольная сила

(),

при =0                  кН;

при =2 м       кН,

в сечениях участков имеем соответственно:

кН,

кН,

кН,

Итак, в четырех сечениях продольные силы отрицательны, что указывает на деформацию сжатия (укорочения) всех участков колонны. По результатам вычислений строим эпюру продольных сил  (рис. б), соблюдая масштаб. Из анализа эпюры следует, что на участках, свободных от нагрузок, продольная сила постоянна, на нагруженных – переменна, в точках приложения сосредоточенных сил – изменяется скачкообразно.

 

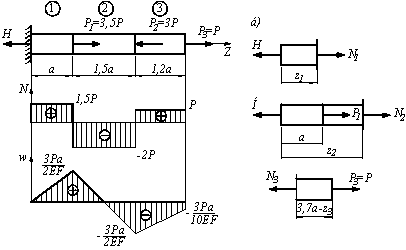
Пример 5. 

Построить эпюру  для стержня переменного сечения (рис. а).

 

Решение.

1. Определяем вид деформации стержня. Все силы лежат на оси стержня, значит, имеем осевое растяжение-сжатие, будем строить эпюру продольных сил N.

2. Проводим ось, параллельную оси стержня.

3. Разбиваем стержень на два участка. В качестве участка загружения будем понимать часть стержня между двумя ближайшими точками приложения сил. Отметим, что изменение площади поперечного сечения не влияет на определение границ участков.

4. Делаем сечения в начале и конце первого участка загружения и определяем N. В сечении 1 (рис. б)  N₁ = F₁ = 6кН;  в сечении 2 (рис. в)  N₂ = F₁ = 6кН. Знак определяем по правилу: N₁, N₂  0, так как сила F₁ растягивает продольные волокна. Откладываем значения N₁, N₂, например, выше оси (строгого правила для продольной силы не существует) и соединяем прямой линией. Внутри ставим в кружочке знак «+» (рис. е). Переходим ко второму участку. В сечении 3 (рис. г) N₃ = F₁ – F₂ = 6 – 10 = - 4кН; в сечении 4 (рис. д)  N₄ = F₁ – F₂ = 6 – 10 = - 4 кН. Поскольку N₃, N₄  0. откладываем полученные значения ниже оси и внутри эпюры ставим в кружочке знак «-». Числовые значения N₁ – N₄ обязательно проставляем на эпюре (рис. е).

5. Эпюру штрихуем и обозначаем.

6. Эпюру проверяем. Так как к стержню не приложены распределенные нагрузки, на эпюре не образуются наклонные прямые. В сечении (1) приложена сила F₁ = 6 кН  на эпюре в этом сечении скачок равный 6; на границе первого и второго участков  приложена сила F₂ =10 кН  на эпюре имеем скачок на величину 6 + 4 =10; скачок, равный 4 в сечении (4) соответствует реакции в заделке, которую мы заранее не определяли. Эпюра построена верно.

 

Пример 6. 

Построить эпюру  для прямого стержня.

Решение.

1. Вид деформации – осевое растяжение-сжатие, строим эпюру N.

2. Проводим вертикальную ось, параллельную оси стержня.

3. Имеем один участок загружения.

4. Делаем сечение в начале и конце участка. В целях упрощения решения задачи оставшиеся после отбрасывания жесткой заделки части стержня, изображать не станем. Будем эту процедуру проделывать мысленно. Для наглядности можно просто закрывать отброшенную часть стержня листом бумаги. Имеем N₁ = 0;  кН.

5. Откладываем N₁, N₂ от оси, например, вправо и соединяем прямой линией (см. рис.).

6. Ставим знак, штрихуем и обозначаем эпюру.

7. Проверка эпюры: так как на стержень действует  равномерно-распределенная нагрузка, на графике должна быть наклонная прямая. Сосредоточенных сил нет, поэтому нет и скачков (скачок в заделке соответствует реакции в заделке).

 

Пример 7. 

Построить эпюру  для стержня переменного сечения.

 

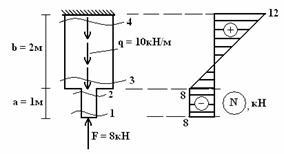
Решение.

1. Вид деформации – осевое растяжение-сжатие.

2. Проводим вертикальную ось.

3. Делим на участки загружения – в данном примере будет два участка.

4. Делаем сечения на первом участке: N₁ = -F= -8 кН; N₂ = -F = -8 кН. Откладываем значения, например, влево от оси, соединяем прямой линией. Делаем сечение на втором участке  кН;   кН. Значение N₃  0, откладываем влево от оси; N₄  0 – вправо и соединяем прямой.

5. Ставим знаки, штрихуем и обозначаем эпюру (см. рис.).

6. Проверка эпюры: на первом участке нет распределенной нагрузки – на эпюре прямая, параллельная оси; на втором участке распределена нагрузка – на эпюре наклонная прямая. В сечении (1) приложена сосредоточенная сила F = 8 кН  на эпюре скачок, равный 8.

 

Пример 8.

Построить эпюру N_z для стержня, приведенного на рисунке.

Р е ш е н и е.

Стержень нагружен только сосредоточенными осевыми силами, поэтому продольная  сила  в пределах каждого участка постоянна. На границе участков N_zпретерпевает разрывы. Примем направление обхода от свободного конца (сеч. Е) к защемлению (сеч. А). На участке DE продольная сила положительна, так как сила   вызывает растяжение, т.е. N_ED = +F. В сечении D продольная  сила  меняется  скачком  от   N_DE = N_ED = F   до  N_DС = N_DЕ –3F = –2F  (находим из условия равновесия бесконечно малого элемента dz, выделенного на границе двух смежных участков CD и DE).

Заметим,  что  скачок  равен  по  величине приложенной силе 3F и направлен  в  сторону отрицательных значений N_z, так как сила 3F  вызывает  сжатие.  На  участке CDимеем  N_СD = N_DС = –2F. В сечении C продольная сила изменяется скачком  от  N_СD = –2F до N_СВ = N_СD + 5F = 3F. Величина скачка равна приложенной силе 5F. В пределах участка CВ продольная сила опять постоянна N_СВ = N_ВС =3F. Наконец, в сечении В на эпюре N_z опять скачок: продольная сила меняется  от N_ВС = 3F  до  N_ВА = N_ВС –2F = F. Направление скачка вниз (в сторону отрицательных значений), так как сила 2F вызывает сжатие стержня. Эпюра N_z приведена на рисунке.

 

Пример 9.

Стержень, нагруженный, как показано на рисунке,  удерживается  в  опоре  силами  трения,  равномерно распределенными по ее толщине. Построить эпюру продольной силы.

 

Р е ш е н и е.

Из условия равновесия стержня в проекции на ось z находим интенсивность сил трения:  

,      ,   откуда   q = 3F/a.

Эпюру N_z строим по формуле . Согласно этой зависимости на участках АВ и CD продольная сила постоянна, так как погонной нагрузки нет (q = 0). На участке  ВС  продольная  сила   изменяется   по   линейному   закону (q = const). В сечениях А и D, где приложены сосредоточенные силы, на эпюре N_z имеют место скачки, равные по величине приложенным силам. Примем направление обхода слева направо. В сечении А сила 2F вызывает сжатие, поэтому    N_AB = 2F. На участке ВС продольная сила изменяется от  N_B = N_A = 2F до . На участке CD продольная сила постоянна и равна  N_СD = 4F.

 

Пример 10.

Стержень, изображенный на рисунке (а), нагружен уравновешенной системой в виде сосредоточенных и распределенных сил. Эпюра продольной силы показана на рисунке (б). Определить значения и направления приложенной к стержню нагрузки.

 

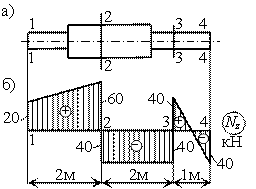
Р е ш е н и е.

В сечениях 1, 2, 3, 4 на эпюре имеются скачки, что связано с приложенными здесь сосредоточенными силами. Скачку вверх соответствует сила, вызывающая растяжение в рассматриваемом сечении; при скачке вниз сила вызывает сжатие. Величина скачка равна приложенной силе. Будем перемещаться по стержню слева направо. В сечении 1 приложена растягивающая сила F₁ = 20 кН, направленная влево. Далее на участке 12 на стержень действует распределенная нагрузка постоянной интенсивности, равной согласно дифференциальной зависимости  тангенсу угла наклона прямой, т.е. q₁₂ =(6020)/2 = 20 кН/м. Погонная нагрузка вызывает растяжение и направлена влево. Приложенная в сечении 2 сила F₂ = 100 кН вызывает сжатие и направлена вправо. На участке 23 распределенной нагрузки нет, так как продольная сила постоянна. В сечении 3 приложена растягивающая сила F₃ = 80 кН (направлена влево). На участке 34 действует  распределенная нагрузка интенсивности  q₃₄ = (40  40)/1 = 80 кН/м, вызывающая сжатие и направленная вправо. Наконец, в сечении 4 приложена сила F₄ = 40 кН, направленная влево.

 

Пример 11.

Стержень переменного сечения с заданным отношением площадей A₁/A₂=2 подвержен действию нагрузок, показанных на рис. а. Цель расчета – подобрать площади поперечного сечения стержня так, чтобы на каждом участке соблюдалось условие прочности. (При этом должно выполняться заданное отношение площадей.)

Решение.

Определяем продольную силу и строим эпюру распределения N вдоль оси стержня. Для этого сначала из уравнения равновесия всего  стержня находим опорную реакцию:

.

Затем, используя метод сечений, определяем продольную силу в произвольном сечении на каждом участке стержня:

на первом участке   ;

на втором участке  ;

на третьем участке  .

Ищем значения N на границах участков. На первом участке продольная сила постоянна и не зависит от x. В начале второго участка

,

в конце второго участка

 .

Аналогично для третьего участка

,      .

По полученным точкам строим эпюру N. На рис. б эпюра N построена для следующих исходных данных:  м,  м; F₁ = 10 кН, F₂ = 40 кН, q₁ = 15 кН/м,q₂ = 20 кН/м.

Зная продольную силу, находим напряжения в стержне и строим эпюру распределения напряжений по длине стержня (рис.  в). Заметим, что на эпюре продольных сил скачки (т.е. резкие изменения усилий при переходе в соседнее сечение) имеют место под сосредоточенными силами на величину этих сил, на эпюре напряжений скачки появляются так же и в местах изменения поперечного сечения.

Для подбора сечения стержня по эпюре напряжений выбираем опасные сечения с максимальными напряжениями. Причем для хрупких материалов важным является не только абсолютное значение напряжения, но и его знак. Более опасным является растягивающее напряжение, так как разрушающее напряжение при растяжении у хрупкого материала много меньше прочности при сжатии. Например, на эпюре , показанной на рис. в, опасным является не только сечение в начале третьего участка , где действуют максимальные сжимающие напряжения, но и сечение в конце третьего участка  с максимальными растягивающими напряжениями. Таким образом, для стержня, показанного на рисунке, должны выполняться условия прочности в трех опасных сечениях:

для чугунной части

,  откуда ,

и  ;

для стальной части

, тогда .

Из трех значений A₁, найденных из условий прочности в опасных сечениях выбираем то, которое удовлетворяет всем условиям. Значение А₂ находим по заданному соотношению: .

Для проверки вычислений находим действительные коэффициенты запаса прочности на каждом участке и сравниваем их с нормируемым коэффициентом запаса. На самом опасном участке (в опасном сечении) действительный коэффициент запаса прочности должен равняться нормируемому, а на остальных участках должен быть больше нормируемого.

 

Пример 12.

Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рисунке. Собственный вес бруса в расчете не учитывать.

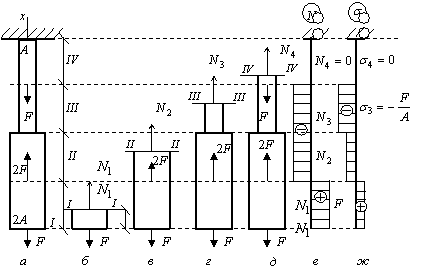
Решение.

Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка.

Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N₁ (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса:

откуда N₁ = F.

Очевидно, что на всем первом участке () нормальная сила N₁ постоянна по величине. Откладываем в масштабе значение нормальной силы N₁ = F в пределах участка I – I (рис. е).

Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N₂  (рис. в). Проектируем все силы на ось бруса:

откуда N₂ = –F.

Аналогично находим нормальные силы в сечении III – III (рис. г):

откуда N₃  = –F

и в сечении IV – IV (рис. д):

откуда N₄ = 0.

Откладывая в масштабе значения нормальных сил N₂, N₃, N₄ в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие.

Для построения эпюры нормальных напряжений  воспользуемся формулой для каждого участка:

Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III).

 

Пример 13.

Определить величину продольной силы  в сечении  I – I бруса, находящегося в равновесии, если  = 20 кН = 2 кг,   = 10 кН = 1 кг,  = 10 кН = 1кг,  = 60º (см. рис.).

                               а)                                                                  б)

 

Решение.

Пользуясь методом сечений:

а) рассекаем брус по заданному сечению;

б) отбрасываем любую, например, правую часть (рис, б);

в) заменяем ее действие на оставшуюся часть неизвестной продольной силой N, направив ее от сечения, т.е. предполагая, что продольная сила – растягивающая;

г) составляем условие  равновесия и вычисляем N:

;  ;

= 1 кг = 10 кН,

т.е. .                                            

Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме проекций на его ось всех внешних сил, приложенных по одну сторону от сечения.

 

Пример 14.

Построить эпюру продольных сил и вычислить диаметр стального короткого бруса, если  = 40 кН = 4 кг,  = 30 кН = 3 кг,  = 80 кН = 8 кг; допускаемое напряжение на растяжение и сжатие принять = 160 МПа = 1600 кг/см² (см. рис.).

Решение.

1. Используя формулу , для каждого из 3-х участков получим (рис. а):

сечение 1 – 1  = – 4000 кг = –40 кН,

сечение 2 – 2 = – 4000 + 3000 = –1000 кг = –10 кН,

сечение 3 – 3 = – 4000 + 3000 + 8000=7000кг = 70 кН.

2. Проводим рядом с брусом ось, параллельную его продольной оси, и, выбрав масштаб, откладываем по длине каждого участка найденные значения продольных сил ,  и , т.е. строим эпюру N (рис. б).

3. Определяем опасное сечение – сечение, в котором нормальные напряжения максимальны (для пластичных материалов берем по абсолютной величине), т.е.

,

где  А – площадь поперечного сечения бруса.

В нашем случае для всех трех участков площадь поперечного сечения А  постоянна и по абсолютной величине N₃>N₂>N₁. Опасное сечение – любое сечение участка 3, где = 7000 кг = 70 кН. Тогда из условия прочности на растяжение и сжатие для расчета площади поперечного сечения применим формулу

;  .

Отсюда

 

Пример 15.

Для стального ступенчатого бруса (), нагруженного осевыми внешними силами F₁ = 150 кН = 15 кг, F₂ = 100  кН = 10 кг, при длине участков = 30 cм, b = 20 см, = 15 см и площади поперечного сечения A = 10 см² требуется:

1. Определить внутренние продольные силы  и построить их эпюру.

2. Вычислить для каждого участка напряжения и построить их эпюру.

3. Выполнить полную абсолютную деформацию бруса и определить перемещение сечения I – I (см. рис.).

                              а)                                        б)                                  в)

 

Решение.

1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, имеем

=  = 15·10³ кг = 150 кН (растяжение);

для второго участка:

=   –  = 15 – 20= –5 кг = –50 кН (сжатие).

Выбираем масштаб и строим эпюру  (рис. б).

2. Вычисляем нормальные напряжения.

На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см². Тогда

на участке с:

Выбираем масштаб и строим эпюру  (рис. в).

2. Полная деформация бруса:

= 0,00973 – 0,00375 = 0,00562 см = 0,0562 м.

3. Поскольку верхнее сечение защемлено, то перемещение заданного сечения I – I численно будет равно абсолютной деформации участков бруса b и c, т.е.

 

 

Пример 16.

Стальной стержень (МПа) находится под действием внешних силы Р₁ и Р₂ (рис. а).

Требуется:

1. построить эпюры продольных сил N, нормальных напряжений σ и перемещений сечений ;

2. определить насколько изменится длина всего стержня если дано: Р₁=2 кН; Р₂=3,2 кН , =160 МПа.

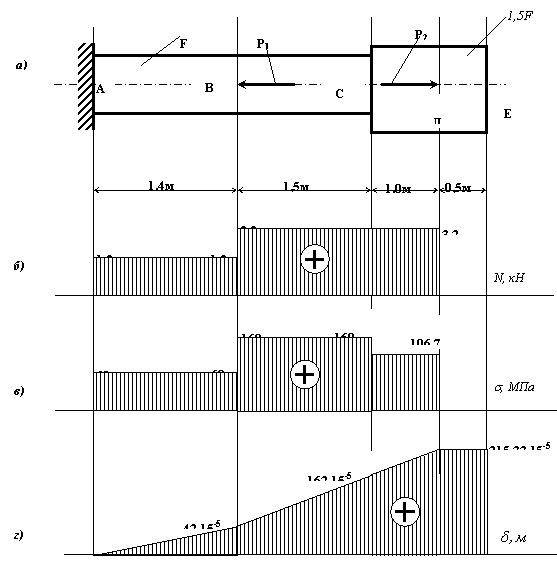
Решение.

Построение эпюры продольных сил

Эпюра продольных сил N приведена на рис. б.

Условие прочности отсюда  

Участок АВ

.

Участок ВС

.

Участок ДС

.

Окончательно принимаем .

Построение эпюры нормальных напряжений 

По данным значениям строим эпюру  рис. в.

Построение эпюры .

Деформация участка 

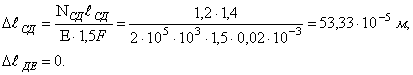
Деформации характерных сечений 

Эпюра  показана на рис. г. Длина всего стержня увеличится на 

 

Пример 17.

Стальной стержень (модуль Юнга  кН/см²) с размерами  см;  см,  см и площадью поперечного сечения нижнего участка  см², а верхнего –  см² нагружен внешними осевыми силами  кН и  кН (см. рис.). Построить эпюры продольных сил  и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести)  кН/см², а допускаемый коэффициент запаса .Найти удлинение стержня .

 

Решение.

1.       Определяем значение опорной реакции , возникающей в заделке.

Учитывая, что , направим опорную реакцию  вниз. Тогда из уравнения равновесия  находим:

кН.

2.        Строим эпюру продольных сил .

Разбиваем длину стержня на три участка (рис. а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.

Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольном месте каждого из трех участков стержня.

Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила  растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила  уравновесит внешнюю силу . Поэтому очевидно, что

кН.

Переходим к сечению 2 – 2 (рис. в). Внешняя сила  растягивает рассматриваемую нами нижнюю часть стержня, а сила  ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна: 

кН.

Делаем сечение 3 – 3 (рис. г). Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила  должна уравновесить внешнюю (реактивную) сжимающую силу R. Поэтому она направлена к сечению и равна:

кН.

Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила  также противодействует сжатию. Она равна:

кН.

При построении эпюры продольных сил  будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.

Это правило знаков вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.

Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна  кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому  кН.

Для построения эпюры продольных сил  проводим тонкой линией ось, параллельную оси стержня z (рис. д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.

Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.

Полученную эпюру обводим жирной линией.

Анализируя полученную эпюру, мы видим, что в местах приложения  внешних сил на эпюре  имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. д, никак не сказывается на характере эпюры .

3.  Строим эпюру нормальных напряжений .

Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле

,

где  и  – продольная сила и площадь k–го поперечного сечения стержня соответственно.

В первом поперечном сечении стержня нормальное напряжение равно

кН/см²,

во втором –

кН/см²,

в третьем –

кН/см².

Строим по вычисленным значениям эпюру  (рис. е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на  эпюре  «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.

4.   Оцениваем прочность стержня.

Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда

кН/см².

Условие прочности имеет вид . В нашем случае

кН/см² >  кН/см²,

следовательно, прочность стержня на втором участке не обеспечена.

Таким образом, площадь поперечного сечения стержня на втором участке, равную  см², нам необходимо увеличить.

Несложный анализ показывает, что на других участках стержня условие прочности выполняется.

Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:

см².

Принимаем на втором участке  см². 

5. Вычисляем удлинение всего стержня .

При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле

,

где E – модуль Юнга, а – длина соответствующего участка стержня.

Тогда

см.

Таким образом, длина стержня уменьшается на 1,7 мм.

 

Пример 18.

Для   стального   ступенчатого   бруса   (см. рис.1) ( МПа), нагруженного силами, кратными F= 30 кН, с длиной участков  l= 0,4 м  при  допускаемом  нормальном   напряжении = 160 МПа требуется:

1. Определить величину продольных сил на каждом участке бруса и построить их эпюру.

2. Подобрать площади поперечных сечений для каждого участка бруса.

3. Вычислить полную деформацию бруса  и построить эпюру перемещений.

4. Определить перемещение заданного сечения А-А.

                                                          N, кН                   , м

                                            а)                                                  б)                                          в)

                                                                                      Рис.1

 

Решение.

1. Определение величины продольных сил. Разбиваем брус на четыре участка и определяем продольные силы N.

Участок KL: рассекаем брус поперечным сечением и отбрасываем ту его часть, на которой расположена заделка. Заменяем ее действие неизвестной, продольной силой N₁, предположительно направив ее  на растяжение, т.е. от сечения (рисунок 2). Составляем уравнение статического равновесия, выбрав положительное направление осиZ, и  определяем величину продольной силы N₁:

;       N₁ = 0;

                          Рис. 2                                                                   Рис. 3

 

Участок DK: аналогично  участку KL делаем сечение в любом месте по длине участка  DK; отбрасываем верхнюю часть с заделкой, заменяем верхнюю отброшенную часть бруса  неизвестной продольной силой N₂ , также направив ее на растяжение (рисунок 3) и составляем условие статического равновесия: 

;        2F + N₂ = 0;

N₂ = - 2F = -230 = - 60 кН.

Отрицательное значение продольной силы N₂ говорит о том, что действительное направление этой силы противоположное, т.е. не на растяжение, а на сжатие. Исправляем свою ошибку, направив силу N₂ в обратную сторону, и отбросив минус в ее значении.

                            Рис. 4                                                                   Рис.5

 

Участок СD:  продольную силу N₃ определяем аналогично определению продольных сил на участках KL и DK (рисунок 4).

;    2F – 5F+ N₃  = 0;  

N₃ = 5F –2F = 3F = 3 30 = 90 кН.

В данном случае получили знак продольной силы N₃ положительный. Это говорит о том, что выбранное направление силы N₃ сделано верно .

Участок ВC: для расчетной схемы (рис. 5) аналогично выше изложенному получаем:     

;      2F – 5F - F+ N₄ = 0;

N₄ = 5F + F – 2F = 4F = 430 = 120 кН.

Знак  у продольной силы N₄ положительный – направление ее выбрано верно.

Далее строим  эпюру  продольных сил. Условимся откладывать положительные значения продольных сил справа от оси, а отрицательные (сжимающие) – слева от оси (рисунок 4,б):

1. Участок KL: продольная сила N₁ = 0;

2. Участок DK: продольная сила N₂ = 60 кН вызывает  сжатие. Следовательно, откладывается в отрицательную сторону.

3. Участок СD: величина продольной силы N₃ = 90 кН, она направлена на растяжение и, соответственно, откладывается в положительную сторону от оси эпюры.

4. Участок ВС: здесь продольная сила N₄ = 120 кН растягивает стержень и откладывается в положительную сторону.

Правило проверки эпюры продольных сил:  в точке приложения к брусу внешней  сосредоточенной нагрузки на эпюре появляется скачок, равный величине внешней нагрузки и  направленный в сторону действия этой нагрузки.

2. Подбор площадей поперечных сечений для каждого участка бруса. Величины площадей поперечных участков находятся из условия прочности при растяжении и сжатии.

;    отсюда .

Участки KL и DK: Площади поперечных сечений участков KL и DK, согласно расчетной схемы, одинаковы и будут равны

Участок СD:

Участок ВС:

3. Вычисление полной деформации бруса  и построение эпюры перемещений.

Полная деформация бруса равна алгебраической сумме деформаций его участков:

.

Для определения полной деформации бруса необходимо определить деформации всех отдельных участков.

Абсолютное линейное удлинение (укорочение) участка бруса длиной l согласно закону Гука равно:

Определяем деформации отдельных участков.

Участок KL:    т.к. N₁ = 0;

Участок DK: 

Участок CD: 

Участок ВC: 

Полная линейная деформация бруса будет равна:

 (0 – 0,32 + 0,32 + 0,32 + 0,32)10^-3 = 0,3210^-3м.

Построение эпюры перемещений начинаем от защемления (сечения В), т.к. по условию задачи это сечение не может перемещаться, т.е. .

Перемещение сечения С численно будет равно деформации участка ВС:   м.

Для остальных участков аналогично получим:

;

;

.

Построение эпюры перемещений (рис.1, в) выполняется аналогично построению эпюры продольных сил; проводим ось эпюры перемещений параллельно оси стержня и откладываем в выбранном масштабе значения величин перемещений сечений бруса с учетом их знаков и соединяем их прямыми линиями.

4. Определение перемещения заданного сечения. Перемещение заданного сечения А-А будет складываться из перемещения точки D и деформации отрезка длиной l₀(рис. 1,а):

;

.

На расчетной схеме рисунок 1 проводим на уровне сечения А-А линию до пересечения ее с эпюрой перемещений . Эта линия должна отсечь на этой эпюре отрезок, равный вычисленному значению   м (см. рис.1,б).

 

Пример 19.

Для изображенного на рис. а стержня простроить эпюру нормальных сил и перемещений поперечных сечений.

а)         в)         г)

Решение.

1. Определение опорной реактивной силы

Уравнение равновесия сил, направленных по оси Z, имеет вид

,

откуда

.

2. Определение внутренних нормальных сил N  методом сечений и построение эпюры N(z)

Стержень имеет три участка, границами которых служат сечения, где приложены внешние силы . Для обнаружения нормальных сил на этих участках используем метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях  и рассматриваем равновесие одной из частей рассеченного стержня, заменяя действие отброшенных частей внутренними нормальными силами  (рисунок 1, б). В результате получаем уравнения равновесия

.

С учетом   находим

.

Нормальные силы на каждом из участков известны, что позволяет легко построить график-эпюру нормальных сил (рис. в).

Из эпюры находим опасное сечение или участок, где нормальные силы максимальны. Таким оказывается второй участок, на котором

.

3. Расчет на прочность

Для опасных сечений второго участка составляем условие прочности

.

Различают три типа расчета на прочность.

 

Проверочный расчет на прочность

Известны все величины в условии прочности. Пусть, например .

Тогда

,

что меньше допускаемого значения . Следовательно, стержень удовлетворяет условию прочности.

 

Проектировочный расчет на прочность

Требуется найти диаметр  круглого поперечного сечения стержня, для которого площадь сечения определяется формулой .

Тогда

,

тогда

.

 Сохраняя значения , получаем

.

Округляя, принимаем .

Расчетное напряжение

, что меньше допускаемого на 5,8 %.

 

Определение допускаемой нагрузки

Имеем

.

Пусть , тогда

.

4. Построение эпюры перемещений

Поскольку в задаче мы имеем три участка с различными значениями нормальных сил, то формулу удобно записать в виде

,

где  – номер участка; – постоянная в начале i-го участка; – текущая координата сечения i-го участка; – жесткость i-го участка, – координаты начального сечения i-го участка.

На первом участке  имеем

.

Следовательно, эпюра − прямая линия.

При  имеем  , т. е.   при жестком защемлении.

При  получаем

.

На втором участке имеем

.

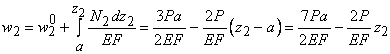Эпюра на втором участке − прямая линия.

При  получаем

.

На третьем участке  имеем

.

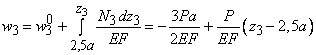При  получаем

.

Используя полученные данные, строим график-эпюру перемещений  поперечных сечений (рисунок 1, г).

5. Расчеты на жесткость

Согласно (5), полное удлинение стержня не должно превышать условия жесткости стержня:

.

Отсюда можно найти другое допускаемое значение силы:

.

Сравнивая два значения, видим что Р_доп  наименьшее.

 

Пример 20.

Построить эпюры  для стержня, изображенного на рисунке, при нагружении силой P и равномерно распределенной нагрузкой q. Составить условие прочности.

а)                     в)             г)

 

Решение.

1. Определение опорной реакции

Уравнение равновесия сил (рис. а)

,

откуда  .

2. Определение внутренних усилий  методом сечений

Стержень содержит два участка с разным характером нагружения. На первом участке делаем сечение на расстоянии  и из условия равновесия левой отсеченной части находим (рисунок 1, б)

.

Следовательно, на первом участке график-эпюра  прямая линия.

Строим эпюру по двум точкам. При  имеем , а при  получаем .

На втором участке отсекаем на расстоянии  правую часть стержня. Действие левой части на правую заменяем усилием  (рис. б). Из уравнения равновесия отсеченной части правой части находим

.

Следовательно, на втором участке  имеем постоянное значение.

Эпюра  приведена на рис. в. На расстоянии  усилие . Найдем это расстояние:

; .

Максимальное значение  возникает в защемлении. Это сечение является опасным по прочности.

Контроль правильности построенной эпюры осуществляется с помощью правил дифференциальной зависимости Д. Журавского

:

1) на незагруженном участке  и ;

2) на равномерно загруженном участке и , т.е. эпюра − прямая линия, возрастающая с ростом , если угловой коэффициент

, и убывающая, если .

Оба правила в нашей задаче соблюдены.

3. Расчет на прочность

Условие прочности стержня

.

Пусть поперечное сечение стержня − прямоугольное с соотношением сторон . Тогда .

Допускаемое напряжение  (дерево), , . Требуется определить размеры поперечного сечения h и b. Тогда:

,

откуда  .

Округляем значение  до значения , тогда  . Проверяем стержень на прочность с подобранными размерами поперечного сечения:

,

что больше допустимого значения .

Перенапряжение составит , т.е. . Отклонение от  допускается в пределах .

4. Построение эпюры перемещений 

На первом участке:

,

или

.

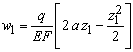Эпюра – парабола. В сечении , где , перемещение достигает максимального значения:

.

Выпуклость параболы определяется знаком второй производной , т.к. . Следовательно, кривая перемещений обращена выпуклостью к верху.

При  имеем

.

На втором участке  получаем

.

Эпюра − прямая линия. При имеем , а при 

.

Строим прямую линию на втором участке (рис. г). Задача решена.

 

Определение напряжений и перемещений в брусе при растяжении-сжатии с учетом собственного веса

Пример 21.

Определить диаметр d, а также удлинение участка CD для круглого стержня, нагруженного силой F, принимая во внимание собственный вес. Удельный вес , допускаемое напряжение  и модуль упругости Е материала стержня заданы.

Решение

Для призматического стержня при действии собственного веса и сосредоточенной  силы   F  на свободном конце имеем:

- продольная  сила  в  произвольном сечении

,

- нормальное напряжение в этом же сечении

.

Из условия прочности находим искомый диаметр

и  ,

oткуда    .

Удлинение участка CD находим по общей формуле

.

Здесь    – это площадь трапеции mnrs, которая равна

.

Следовательно,   .

 

Пример 22.

Стержень переменного сечения с соотношением площадей поперечных сечений A₁/A₂ =2 находится под действием сосредоточенных сил и собственного веса (рис. а). Материал стержня на всех участках одинаков. Требуется построить эпюры распределения продольной силы и напряжений вдоль оси стержня и определить перемещение сечения а–а.

Решение.

Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.

на первом и втором участках

,

на третьем участке

,

где  – объемный вес материала стержня.

Эпюры продольной силы и напряжений строим, используя метод сечений. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A₁ по условию больше, чем A₂ (рис. б). Угол же наклона эпюры напряжений зависит от объемного веса , и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. в).

Находим перемещение (опускание) сечения а–а. Это перемещение можно искать разными способами. По первому способу для определения перемещения используем формулу . Здесь F – сосредоточенная сила, вызывающая перемещение участка длиной l; G  – собственный вес рассматриваемого участка. Эту формулу можно использовать на участках постоянного сечения между сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е. заделки. Например, в рассматриваемой задаче перемещение сечения а–а складывается из удлинения участка длиной l₁, которое мы обозначим , и удлинения участка длиной . При определении удлинения  в формуле сила F равна сумме F₁, F₂ и собственного веса всех расположенных ниже участков. Вес участка стержня длиной l₁: . Таким образом, по формуле

.

Удлинение  происходит под действием сосредоточенной силы, состоящей из силы F₂, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка . То есть

.

Окончательно опускание сечения а–а равно .

Если построена эпюра распределения напряжений, то для определения перемещения заданного сечения удобно использовать второй способ, применяя формулу . В этой формуле , а  – это площадь эпюры напряжений. Таким образом, если найти площадь  двух трапеций на участке между неподвижным сечением (заделкой) и сечением а–а (заштрихованные площади и эпюры  на рис.  в) и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:

.

При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.

 

Пример 23.

Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рис. а. Принять a = 0,4 м; площадь поперечного сечения  бруса на участкахIII и IV А = 20 см²; сосредоточенная сила F = 0,5 кН, собственный вес = 0,0078 кг/см³ = 76,44 кН/м³.

Решение.

Для определения внутренних усилий разбиваем брус с прямолинейной осью на четыре участка. Проводим сечение I – I (рис. а) и отбрасываем верхнюю часть бруса, заменяя действие отброшенной части нормальной силой N₁ (рис. б). Так как сечение I –I может быть проведено в любом месте участка I, то длина оставшейся части участка будет переменной величиной, и поэтому обозначим ее через x (рис. б), причем . Запишем уравнение равновесия, проектируя силы, действующие на оставшуюся часть бруса, на направление оси бруса:  

       а                    б                   в                   г                д                      е                 ж  

 

откуда 

Через  обозначен собственный вес оставшейся части бруса первого участка, в пределах которого площадь поперечного сечения равна 2А, а длина оставшейся части обозначена через x. Подставим численные значения в полученную формулу:

.

Записанное выражение показывает, что эпюра нормальных сил в пределах первого участка представляет собой наклонную прямую линию. Для построения этой прямой определим значение нормальной силы N₁ в начале первого участка (x = 0): N₁(x = 0) = 500 Н и в конце первого участка (x = a= 0,5 м):  N₁ (х = 0,5 м) =

Полученные значения откладываем в масштабе в соответствующих точках эпюры нормальных сил (рис. е). Найденные точки соединяем прямой линией, затем штрихуем первый участок эпюры прямыми линиями, перпендикулярными к оси бруса.

Проводим сечение II – II и повторяем порядок расчета, описанный выше для сечения I – I. Переменная величина х участка II – II будет изменяться в пределах . Составим уравнение равновесия (рис. в)

откуда 

где – собственный вес части бруса, расположенного ниже сечения II – II.

Окончательно имеем

Определяем значение нормальной силы N₂ в начале второго участка (х= 0,5 м):

и в конце этого же участка (х = х_max = 1 м):

Полученные значения N₂ откладываем в масштабе в начале и в конце второго участка (рис. е).

Проводим сечение III – III и для оставшейся части бруса составляем уравнение равновесия (рис. г)

откуда  где  – собственный вес оставшейся части бруса третьего участка; – собственный вес первого и второго участков.

Тогда для участка 

где нормальная сила N₃ в начале третьего участка будет N₃(х=0) = –194,2 Н; а в конце третьего участка получаем N₃ (х = a = 0,5 м) = –117,8 Н. Найденные значения N₃переносим на эпюру нормальных сил.

И наконец, рассматривая равновесие оставшейся части бруса, после проведения сечения IV – IV получаем (рис. д)

откуда  где  Н – собственный вес участков I – I и II – II, – собственный вес третьего и оставшейся части четвертого участков.

В этом случае имеем

т.е. в начале четвертого участка N₄ (х = 0,5 м) = 382,2 Н, а в конце этого же участка N₄ (х = 1 м) = 458,64 Н. Вычисленные значения N₄ откладываем в масштабе на эпюре нормальных сил (рис. е).

Эпюра нормальных сил показывает, что первый и четвертый участок подвержены растяжению, а второй и третий – сжатию.

Для вычисления значений нормальных напряжений  и построения эпюры нормальных напряжений используем формулу:

Эпюра нормальных напряжений показывает, что самое большое нормальное напряжение возникает в сечении, проходящем через точку Л четвертого участка (рис. ж), т.е. на опоре.

 

Пример 24.

Дано: брус постоянной жёсткости (см. рис.) длиной 2l, площадью поперечного сечения A, нагружен сосредоточенной силой F, распределённой нагрузкой интенсивностью q и собственным весом.

Требуется: построить эпюру N.          

                                                                                                                                                                         Эп N

 

Решение.

1. Определение опорной реакции

Составим сумму проекций всех сил на продольную ось бруса Z:

2. Установление силовых участков

Изучив действие внешних нагрузок F, , q на брус, нетрудно установить, что имеется два силовых участка:

- первый участок, , на котором N зависит от F и ;

- второй участок, , на внутреннюю силу N оказывают влияние F, ,q.

3. Составление аналитических выражений для нормальной силы

С учётом метода сечений брус рассекаем на две части, отбрасываем верхние отсечённые части, заменяя их действие силами. Целесообразно силы N₁ и N₂направить по внешней нормали к сечению, то есть предполагать, что они вызывают растяжение бруса.

4.  Вычисление значений N в характерных сечениях бруса

Определим значения N на границах силовых участков:

- при ;

- при .

- при ;

- при .

- при ;

.

По полученным результатам расчёта строим эпюру N с учётом масштаба (см. рис.).

Примечание. В расчётно-проектировочной работе необходимо результаты расчётов доводить до числовых величин. Для проверки правильности построения эпюры Nнужно воспользоваться следующими дифференциальными зависимостями:

.

 

Перемещения поперечных сечений брусьев в статически определимых задачах при растяжении-сжатии

Пример 25.

Определить перемещение нижнего конца стержня, изображенного на рис. а. Задачу решить без учета собственного веса материала бруса. Принять  a= 0,5 м; А = 10 см²; сосредоточенная сила F = 10 кН.

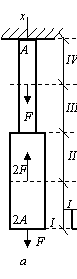
Решение.

Для рассматриваемого случая эпюра нормальных сил представлена на рис. е. Для стержня со ступенчатым изменением площади и нормальных сил перемещения поперечных сечений вычисляются по формуле (1.7). Рассматривая рис. а и рис. е, запишем формулу для определения перемещения нижнего конца стержня в виде:

Знак «минус» в ответе показывает, что общая длина стержня уменьшится, т.е. нижний конец стержня переместится вверх вдоль его оси на величину мм.

 

Пример 26.

Определить перемещение нижнего конца стержня, изображенного на рис. а. Принятьобъемный вес материала стержня = 76440 Н/м³.

 

Решение.

Для рассматриваемого случая эпюра нормальных сил представлена на рис. б.

Эпюра нормальных сил построена с учетом сосредоточенных внешних сил и с учетом собственного веса материала бруса. Выделим на эпюре нормальных сил (рис. б) ее постоянные нормальные составляющие и треугольные участки эпюры, учитывающие собственный вес соответствующего участка. Разделение составляющих эпюры нормальных сил на рис. б произведено пунктирными линиями.

Теперь перемещение поперечного сечения от постоянной составляющей эпюры нормальных сил будет определяться по формуле  а перемещение от действия собственного веса – по формуле  

Для рассматриваемого случая формула для определения перемещения нижнего конца стержня будет иметь вид

 

  Знак «+» показывает, что общая длина стержня увеличится, т.е. нижний конец стержня переместится вниз вдоль его оси на величину м (рис.  а).

  Определим перемещение сечения а – а (рис. а). Для этого мысленно разрежем эпюру нормальных сил в соответствующем сечении а – а и отбросим нижнюю часть эпюры. На основании оставшейся части эпюры нормальных сил (рис. в) определяем перемещение сечения а – а, используя формулы  и 

Полученный ответ показывает, что поперечное сечение а – а переместится вниз вдоль оси стержня.

 

Пример 27.

Для стального бруса квадратного сечения сжатого силой Р с учетом собственного веса при исходных данных приведенных ниже, требу­ется (см. рис. а):

1. Определить количество расчетных участков;

2. Составить аналитические выражения для нормальных сил N_z , нормальных напряжений  и вычислить их значения для каж­дого из участков с учетом их собственных весов;

3. Построить эпюры N_z и ;

4. Вычислить перемещение верхнего конца колонны от дейст­вия силы Р и собственного веса.

Дано: Р = 20 кН; l₁ = l₂ = l₃ = 0,4 м; модуль упругости стали Е =  кН/м²; F₁ =  м²; F₂ =  м²; F₃ =  м²;  = 78 кН/м³ .

Решение.

1. Определение количества участков. Так как нор­мальная сила N_z зависит от величин внешних сил, в данном случае включающих в себя и собственный вес колонны, а последний, в свою очередь, от размеров попе­речного сечения F_i и объемного веса , то границами участков следует назначать те сечения, в которых приложены внешние сосредоточенные силы и где происходит скачкообразное изменение площади попе­речного сечения или объемного веса материалов конструкций.

Исходя из вышесказанного, учитывая const, брус будет иметь три участка:

1 участок  от 0 до сечения В (где приложена сила Р);

2 участок  от сечения В до сечения С;

3 участок  от сечения С до сечения D.

Следует заметить, что при определении нормальных напряже­ний используются те же участки.

 

2. Составить аналитические выражения для нор­мальных сил N_z, нормальных напряжений _z и вычис­лить их значения для каждого из участков, с учетом их собственных весов. Для этого воспользуемся методом сече­ний.                

1 участок (0  В) .

Проведя сечение 1  1 на расстоянии z₁ от начала координат (точка 0), рассмотрим равновесие верхней части. При этом, к рас­сматриваемой части прикладываются в центре ее тяжести собствен­ный вес и нормальная сила , заменяющую действие отброшен­ной нижней части бруса на верхнюю рассматриваемую (рис. б). Составив уравнение равновесия рассматриваемой верхней части ко­лонны по оси z , получим:

.

В свою очередь, собственный вес верхней части колонны оп­ределяется следующим образом:

кН.

Тогда выражение для нормальной силы будет иметь вид:

кН,

а для нормальных напряжений :

кН/м2.

Так как,  и линейно зависят от z₁ , то для построения их графиков (эпюр) достаточно определить значения этих величин на границах участка, т.е.

при z₁ = 0              

при z₁ = 0,4 м       кН;

                                кН/м².

Знаки минус при  и указывают на то, что принятое на­правление для этих величин не совпадает с действительным, т. к. в принятой схеме продольная сила не растягивает, а сжимает первый участок.

2 участок (В  С)  .

Аналогично предыдущему проводим сечение 22 на расстоянии z₂ (рис. в). Для верхней части составляем уравнение равновесия .

В это уравнение войдут: собственный вес первого участка ; собственный вес отсеченной части второго участка  ; сосредоточенная сила Р = 20 кН, а также сила .

Тогда уравнение равновесия примет вид:

,

отсюда

= =  кН.

Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть запи­сано таким образом:

кН/м².

Вычислим значения ординат  и  в граничных сечениях второго участка:

при z₂ = 0,4 м        кН,

                                                кН/м²;

при z₂ = 0,8 м        кН,

                                                кН/м².

3 участок (С  D)  .

Составив уравнение равновесия  (рис. г) для верхней части бруса, получим:

,

откуда

кН.

Выражение для напряжения:

кН/м².

Вычислим значения ординат  и  в граничных сечениях третьего участка:

при z₃ = 0,8 м       (0,8) = 19,5 (0,8 + 0,43364) = 24,056 кН,

                                (0,8) = 78 (0,8 + 0,43364) = 96,224 кН/м²;

при z₃ = 1,2 м       (1,2) = 19,5 (1,2 + 0,43364) = 31,856 кН,

                                кН/м².

3. Построение эпюр N_z и. По причине линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений N_z и  в граничных сечениях каждого из участков (см. рис. д, е). Необходимым условием правильности построения этих графиков является выпол­нение следующих требований:

 скачок в эпюре N_z должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;

 скачки в эпюре  должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения ко­лонны.

После анализа полученных эпюр (рис. д, е) легко можно убедиться, что построения выполнены правильно.

4. Вычисление перемещения верхнего конца ко­лонны от действия всех сил. Полное перемещение со­гласно закону Гука может быть вычислено по формуле

.

В данном случае это выражение принимает следующий вид:

Так как величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными функциями, то для вычисления перемещений  достаточно вычислить площади эпюры N_z на каждом из этих участков и разделить их на E_i F_i . Следовательно,

.

 

Пример 28.

Найти закон изменения площадей поперечного сечения бруса равного сопротивления, испытывающего растяжение под действием силы  и собственного веса.

Решение.

В каждом сечении бруса равного сопротивления нормальные напряжения должны быть равны постоянной величине (). Запишем условие равновесия элемента длиной dx:

или 

Имеем dG – собственный вес элемента бруса длиной dx:

тогда   или 

Интегрируя последнее выражение, находим

где С – произвольная постоянная интегрирования, которая находится из граничных условий. Окончательно запишем

Постоянную интегрирования находим из условия, что при х = 0 имеем А(х) = А₀, т.е. получаем .

Таким образом, закон изменения площади поперечного сечения А(х) получает вид

,

т.е. в брусе равного сопротивления площади поперечных сечений изменяются по логарифмическому закону.

 

 

Задачи для самостоятельного решения

Задача №1

Стяжка диаметром 25 мм растянута усилием F (см. рисунок), вызывающим в ней напряжение 100 МПа. Чему должен равняться диаметр шайбы d, чтобы давление, передаваемое ею на стену, не превышало 1,4 МПа?

Ответ: 213 мм

 

Задача № 2

Медная проволока диаметром 1,2 мм удлиняется на 0,25 мм под нагрузкой 90 Н. Определить длину проволоки.

Ответ: 314 мм.

 

Задача № 3

Стержень из малоуглеродистой стали шириной 0,3 м и толщиной 0,015 м ослаблен заклепочным отверстием диаметром 0,023 м, расположенным на оси стержня. Какое растягивающее усилие этот стержень может выдержать, если допускаемое напряжение равно 90 МПа?

Ответ: 374 кН.

 

Задача № 4

Определить напряжения во всех участках изображенного на рисунке стального стержня и полную его деформацию, если поперечное сечение равно 1∙10^-3 м².

Ответ: на левом участке  =40 МПа; на среднем  = 20 МПа; на правом = 20 МПа;  = 0.

 

Задача № 5

Стальная полоса (см. рисунок) растянута продольными силами. Она ослаблена круглыми заклепочными отверстиями, как показано на рисунке. Определить среднюю величину напряжений в опасном сечении.

Ответ: 100 МПа.

 

Задача № 6

К нижнему концу троса, закрепленного верхним концом, подвешен груз  F = 75 кН. Трос составлен из проволок диаметром d = 2 мм. Допускаемое напряжение для материала троса равно [] = 300 МПа. Из какого количества проволок должен быть составлен трос?

Ответ: 80 проволок.

 

Задача № 7

Определить напряжения в обеих частях изображенного на рисунке стержня, а также полное его удлинение. Материал стержня — сталь, сечение круглое.

Ответ: в левой части  =127,6 МПа; в правой  =31,9 МПа;  = 0,575 мм.

 

Задача № 8

Определить напряжение в шатуне автомобильного двигателя, поперечное сечение I – I которого (см. рис.) имеет форму двутавра, и проверить прочность при допускаемом напряжении [] = 140 МПа. Найти число шпилек n для крепления головки цилиндра,  если внутренний диаметр резьбы d_В = 8 мм, []=80 МПа. Диаметр цилиндра D = 80 мм, давление газов р = 3,6 МПа.

Ответ. Напряжение  = 144 МПа,   = 2,85%, что допустимо, число шпилек п = 5.

 

Задача № 9

Определить допускаемую нагрузку для стального листа толщиной t=10 мм, если допускаемое напряжение [] = 100 МПа (см.рис.), размеры в миллиметрах.

Ответ. Допускаемая нагрузка [F]= 140 кН.

 

Задача № 10

Определить напряжение в точке О, а также величину растягивающей силы F, зная напряжение в точке К, равное 100 МПа.

 

Задача № 11

При растяжении стержня силой F = 800 кН в точке К с координатами Х_к = 4 см и У_к = 3 см возникает напряжение 160 МПа. Чему равен диаметр стержня?

 

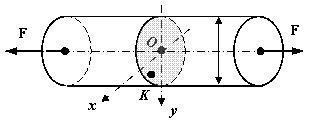
Задача № 12

Как изменится абсолютное удлинение бруса, если:

а) увеличить линейные размеры b и l в 2 раза;

б) увеличить длину l в 2 раза и заменить материал (например, медь на сталь);

в) уменьшить размер b в 2 раза, длину l в 4 раза и заменить материал (например, сталь на титан);

г) уменьшить в 3 раза линейные размеры b, l и силу F?

 

Задача № 13

Вертикально подвешенный резиновый жгут под действием некоторого груза, прикрепленного к нижнему свободному концу, удлиняется на 16 см. Затем он дважды складывается пополам и к сложенному таким образом жгуту прикладывается тот же самый груз. Насколько удлинится жгут в этом случае?

 

Задача № 14

Жесткость стального провода равна 10 Н/мм. Чему равно удлинение троса, сплетенного из 10 таких проводов, если к концу троса подвесить груз весом 2 кН?

 

Задача № 15

При буксировке автомобиля массы 1т результирующая сил сопротивления и трения в 50 раз меньше веса автомобиля. Чему равна жесткость троса, если при равномерном движении автомобиля трос удлиняется на 20 мм?

 

Задача № 16

Определить ширину фундамента здания, учитывая, что среднее напряжение в грунте не должно превышать 0,5 МПа. Общий вес фундамента, стены и полезной нагрузки на 1 м длины здания равен 500 кН/м.

 

Задача № 17

Какую нагрузку сможет выдержать короткая гранитная колонна диаметром 80 см, если допускаемое напряжение на сжатие гранита равно [] = 4 МПа?

 

Задача № 18

Стальной стержень кругового поперечного сечения растягивается силой 100кН. При каком наименьшем диаметре стержня относительное удлинение не превышает 5·10^-4 , а напряжение – 120 МПа?

 

Задача № 19

При какой минимальной базе тензометра с коэффициентом увеличения 1000 и точностью отсчета 0,1 мм можно обеспечить измерение напряжений в стальной детали с точностью не менее 1 МПа?

 

Задача № 20

Стальной стержень кругового поперечного сечения диаметром 30 мм растянут на испытательной машине силой 120 кН. Его продольное удлинение, замеренное на длине 50 мм, составило 42 мкм, а изменение диаметра – 7 мкм. Определить модуль упругости и коэффициент Пуассона материала стержня.

 

Задача № 21

Для установки тяжелой колонны в вертикальное положение требуется поднять ее левый конец. К какой точке колонны нужно прикрепить трос, чтобы напряжения в нем были минимальными? Выполнить проверку прочности троса при следующих данных: вес колонны G = 200 кН, ее длина l = 16 м, высота опоры Н = 4 м, площадь поперечного сечения троса А = 24 см² , допускаемое напряжение [] =170 МПа.

 

Задача № 22

Для заданных брусьев построить эпюры продольных сил, напряжений и перемещений. Определить наибольшие напряжения, перемещения и запасы по текучести, полагая  F = qu = 10 кН, А = 2 см² , а = 20 см,  = 200 МПа, Е = 100 ГПа.

 

Задача № 23

Трещины в асфальтированных дорогах возникают чаще всего зимой. Почему?

 

Задача № 24

Чтобы стакан не лопнул при наполнении его кипятком, рекомендуется в него предварительно опустить чайную ложку и лить кипяток на ложку. какую роль играет в данном случае чайная ложка?

 

Задача № 25

На некоторых железных дорогах сваривают рельсы в одну непрерывную нитку. Спрашивается, в каком интервале температур должна быть произведена сварка, чтобы при колебаниях температур от минус 40^оС до плюс 40^оС наибольшие сжимающие напряжения не превышали 75 МПа, а наибольшие растягивающие – 150 МПа, если Е=200 ГПа,=125?

 

Задача № 26

Эпюры N_z для стержней, представленных на рисунке предлагается построить самостоятельно. Для проверки тут же дается решение.

           

 

Задача № 27

Подобрать диаметр бруса, если F₁=3 кН; F₂=5 Кн; F₃=16кН и =140 МПа.

            

Задача № 28

Силу перенести по линии её действия из точки “B” в точку “C”. Что при этом изменится ?

          

 

Задача № 29

Найти продольные силы N на участках стержня, построить эпюру, вычислить напряжения во всех участках представленного на рисунке стального стержня и полную его деформацию. Сила Р = 20 кН, а = 1 м, площадь поперечного сечения стержня F=5 см².

Ответ: На участках слева на право = 80 МПа, = 0,  = - 40 МПа, = 0.

 

Задача № 30

Построить эпюры нормальных сил и нормальных напряжений для бруса постоянного поперечного сечения с А = 10 см². На брус действует внешняя распределенная осевая нагрузка q = 5 кН/м и продольные сосредоточенные силы F= 15 кН (рис.  а).

Ответ: эпюры нормальных сил и напряжений представлены на рис. б, в.

 

Задача № 31

Построить эпюры нормальных сил и нормальных напряжений для бруса постоянного поперечного сечения с А = 10 см². На брус действует внешняя распределенная осевая нагрузка q = 5 кН/м и продольные сосредоточенные силы F= 15кН (рис.  а).

Ответ: правильные результаты показаны на рис.  б, в.

 

Задача № 32

Дан прямой стальной стержень кусочно - постоянного сечения, для которого a = 0,4 м, а площади поперечных сечений указаны на рис.  а.

Построить эпюры нормальных сил и нормальных напряжений. Найти сечение, где действует .

Ответ: эпюры нормальных сил и нормальных напряжений при учете только собственного веса стального стержня представлены на рис. б, в ,= 1,3345 кг/см² в точке С участка с площадью поперечного сечения А₂.

 

Задача № 33

Проверить прочность стального стержня, изображенного на рис. а. Материал – сталь с  R_y = 2450 кг/см² и объемным весом  = 0,00785 кг/см³,  F = 10 т, = 1.

Ответ: = 1429 кг/см² < R_y = 2450 кг/см² (см. рис. в), следовательно, условие прочности выполняется.

 

Задача № 34

Построить эпюру нормальных сил для стержня замоноличенного в массив (рис. а), предполагая, что интенсивность сил трения постоянна по длине a. Собственным весом стержня пренебречь.

Ответ: эпюра нормальных сил показана на рис. б.

 

Задача № 35

Определить площади верхнего А_в0 и нижнего А_в1 сечений, а также вес  кладки из глиняного кирпича в форме бруса равного сопротивления сжатию, если на верхнее сечение действует сосредоточенная сила  F = 3000 кН, высота стойки l = 20 м, R = 1,5 МПа; = 1,00. Объемный вес кладки принять  = 18 кН/м³.

Ответ: А_в0 = 2 м²; А_в1 = 2,54 м²; стойка из глиняного кирпича объемом  м³  весит  = 810 кН.

 

Задача № 36

Получить аналитические выражения для определения напряжений в поперечных сечениях бруса, имеющего форму, показанную. на рисунке. Толщину бруса принять постоянной и равной t = 2 см. Требуется: а) решить задачу, учитывая только собственный вес бруса с = 78,5 кН/м³, а сжимающую силу F принять равной нулю (F = 0); б) решить задачу без учета собственного веса, но принять F = 200 кН; в) решить задачу, принимая F  = 200 кН и, учитывая собственный вес стального бруса с = 78,5 кН/м³. 

Ответ: а) , [Па];    б) , [Па];    в) , [Па].

 

Задача № 37

Стальной стержень квадратного сечения со сторонами a_i, находится под воздействием сосредоточенных сил  F_i, направленных вдоль оси стержня (рис. а).

Определить размеры поперечных сечений стержня так, чтобы в любом сечении стержня действовали нормальные напряжения, равные расчетному сопротивлению R_y= 240 МПа. Собственный вес стержня не учитывать.

Ответ: a₁ =0,91см; a₂ =1,02 см; a₃ =1,29 см; a₄ =1,12 см (рис. б).

 

Задача № 38

Определить допускаемую нагрузку F_adm растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали  принять R_y = 240 МПа,  а = 1. Толщина листа  t =1 см, ширина b = 15 см. 

Ответ: F_adm = 216 кН.

 

Задача № 39

Определить допускаемую нагрузку F_adm растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали  принять R_y = 240 МПа, а = 1. Толщина листа t = 1 см, ширина b = 13 см. 

Ответ: F_adm = 216 кН.

 

Задача № 40

Определить допускаемую толщину t растягиваемого стального листа, изображенного на рисунке, если диаметры отверстий d = 2 см, а ширина листа b = 20 см.Расчетное сопротивление стали принять: R_y = 240 МПа, а = 1. Внешняя растягивающая сила F = 20 т.

Ответ:  см.

 

Задача № 41

В стенке стального двутавра № 20 вырезано отверстие диаметром d = 10 см (см. рис.). Определить допускаемую на-грузку F_adm, которая может быть приложена вдоль продольной оси ослабленного двутавра. Расчетное сопротивление стали принять R_y = 2450 кг/см², а γ_c = 1,1.

Ответ: F_adm = 571 кН.

 

Задача № 42

В стенке стального двутавра № 20 вырезано отверстие диаметром d = 10 см. Определить допускаемую равномерно распределенную нагрузку  (кг/м), которую можно приложить вдоль стенки двутавра (см. рис.). Расчетное сопротивление стали R_y  =  2450 кг/см², а = 1.

Ответ:  = 84933 кг/м = 833,19 Н/м.

 

Задача № 43

Определить перемещение нижнего конца стержня, изображенного на рисунке. Дан прямой стержень кусочно-постоянного сечения,  для которого a₁ = 25 см, a₂ = 15 см, a₃ = 10 см, a₄ = 20 см, А₁ = А = 20 см², А₂ =А₃ =4А, А₄ = 2А. Стержень находится под действием сосредоточенных сил F₁ = 327,2 Н; F₂ = 1 кН; F₃ = 500 Н и собственного веса с = 78,5 кН/м³, действующих вдоль оси стержня. Принять .

Ответ: 

 

Задача № 44

Определить перемещение нижнего конца стержня, представленного на рисунке. Принять а = 0,4 м; объемный вес материала стержня 

Ответ: 

 

Задача № 45

Определить линейную продольную деформацию каждого участка стержня кусочно-постоянного квадратного сечения, изображенного на рисунке. Вычислить перемещение точки С рассматриваемого стержня и построить эпюру перемещений поперечных сечений стержня. Принять a₁ = 0,9 см; a₂ = 1 см; a₃  = 1,3 см; a₄ = 1,1 см.Задачу решить без учета собственного веса стержня, .

Ответ:  мм;    

 

Задача № 46

Стержень постоянного поперечного сечения нагружен сосредоточенными силами (см. рис. а). Построить эпюру перемещений. Собственный вес стержня в расчете не учитывать.

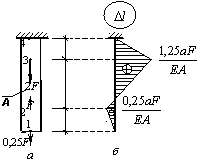
Ответ: эпюра перемещений показана на рис. б.

 

Задача № 47

Прямой стальной стержень с площадью поперечного сечения А = 5 см² закреплен верхним концом, а к нижнему концу приложена растягивающая сила F =30 кН. Определить относительную и продольную линейную деформации, относительную поперечную деформацию , если длина стержня l = 3 м, модуль Юнга , коэффициент Пуассона  = 0,3; удельный вес материала стержня = 78,5 кН/м³.

Ответ:  0,9 мм;  

 

Задача № 48

Определить относительную деформацию в каждом участке стержня постоянного поперечного сечения, показанного на рисунке. Собственным весом стержня при расчете пренебречь.

Ответ: 

 

Задача № 49

Стальной вертикальный стержень из двутавра № 30 растягивается под действием собственного веса. Длина стержня l = 20 м. Определить нормальное напряжение в закрепленном верхнем конце и перемещение  нижнего конца стержня, 

Ответ:  = 0,00785 см.

 

Задача № 50

Вертикальный стержень из двух швеллеров № 20, закрепленный верхним концом, растягивается под действием собственного веса и силы F = 40 т. Определитьмаксимальное нормальное напряжение и перемещение  нижнего конца стержня при модуле продольной упругости  Длина стержня l =4 м. Сила приложена к нижнему концу стержня.

Ответ: =0,171 см.

 

Задача № 51

Стальной болт длиной l = 16 см при затяжке получил удлинение = 0,12 мм. Определить напряжение в болте, если модуль Юнга .

Ответ:    

 

Задача № 52

Алюминиевый стержень круглого поперечного сечения диаметром 10 см растягивается силой F. Найти величину допускаемой силы F_adm, если допускаемое уменьшение начального диаметра =0,002см; коэффициент Пуассона = 0,35.

Ответ: F_adm = 283 кН.

 

Задача № 53

Дан прямой стержень кусочно-постоянного сечения,  для которого a₁ = 25 см, a₂ = 15 см, a₃ = 10 см, a₄ = 20 см, А₁ = А = 20 см², А₂ =А₃ =4А. А₄ = 2А (рис. а). Стержень находится под действием сосредоточенных сил F₁ = 327,2 Н; F₂ = 1 кН; F₃ = 500 Н и собственного веса с = 78,5 кН/м³, действующих вдоль оси стержня.

Требуется построить для заданного стержня эпюры нормальных сил и нормальных напряжений.

Ответ: правильный результат показан на рис. б, в.

 

Задача № 54

Дан прямой стальной стержень кусочно-постоянного сечения, для которого а = 0,4 м, а площади поперечных сечений указаны на рис. а. При учете действия только собственного веса стального стержня эпюры нормальных сил и напряжений имеют вид, показанный на рис. б, в.

Как изменятся эпюры нормальных сил и напряжений, если рассмотреть тот же стержень, но с защемленными обоими концами. Проверить правильность вычислений, используя критерий равенства площадей эпюры  с разными знаками. Найти поперечное сечение, где N = 0, = 0.

Ответ: опорная реакция нижней опоры R = –9,83 кг, следовательно, соответствующие  значения эпюры N, показанной на рис. б, необходимо сложить с величиной R  = –9,83 кг.

 

Задача № 55

Имеются две стальные трубы, одна из которых имеет наружный диаметр D₁ = 102 мм и толщину стенки t₁ = 3 мм, а другая – D₂ = 168 мм, t₂ = 4 мм (см. рис.). Используя справочные данные в сортаменте можно определить, что площади их поперечных сечений равны A₁ = 9,3 см²; A₂ = 20,6 см². Обе трубы имеют длину l = 20 см. Вставленные осесимметрично друг в друга трубы подвергаются сжатию силой F = 20 т. Определить нормальные силы и напряжения, передающиеся на каждую трубу.

Ответ: = 668,9 кг/см² = 65,62 МПа; N₂ = 13779,3 кг =135,2 кН; N₁ =  6220,7 кг = 61 кН.

 

Задача № 56

Имеются две трубы, одна из которых стальная с наружным диаметром D₁ = 102 мм и толщиной стенки t₁ = 3 мм (А₁ = 9,3 см²), а другая алюминиевая с наружным диаметром D₂ = 168 мм и t₂ = 4 мм (А₂ = 20,6 см²). Вставленные осесимметрично друг в друга трубы подвергаются сжатию силой F = 20 т (см. рис.). Определить нормальные силы и напряжения, передающиеся на каждую трубу. Вычислить укорочение труб (), если их длина l  = 20 см, а модуль продольной упругости для алюминия , для стали – Е₁ = 2,1·10⁶ кг/см².

Ответ: N₁ = 11,925 т = 116,98 кН;  = 1282 кг/см² = 125,76 МПа; N₂ = 8,075 т = 79,21 кН;  = 392 кг/см² = 38,45 МПа; = 0,12 мм.

 

Задача № 57

Дана конструкция, состоящая из трех элементов: двух труб разного диаметра и одного сплошного стержня (см. рис.). Все три элемента выполнены из разных материалов с модулями продольной упругости Е₁, Е₂, Е₃. Площади поперечных сечений двух труб А₂ и А₃, а площадь поперечного сечения сплошного стержня А₁. Элементы осесимметрично вставлены один в другой и помещены между абсолютно жесткими плитами. Вся стержневая система сжимается силой F. Требуется определить нормальные напряжения в поперечных сечениях каждого из элементов конструкции.

Ответ: