2.1.2. Оценка предела выносливости при переменном растяжении-сжатии
В связи со сравнительно ограниченным по объему статическим материалом, касающегося испытаний на усталость при симметричном растяжении-сжатии, не представляется возможность надежного обоснования параметров уравнения линии регрессии (2.3) для оценки предела выносливости, как это было рассмотрено в предыдущем параграфе применительно к переменному изгибу образцов.
В этом разделе рассмотрен другой подход к вопросу оценки предела выносливости рассматриваемых конструкционных материалов и вычисление средней квадратической ошибки его расчета.
На
основании существующих литературных
данных произведены оценки среднего
значения 
и
среднего квадратического
отклонения 
отношения 
для
каждого класса рассмотренных
конструкционных материалов по формулам
и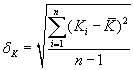 
(2.16)
Здесь 
и
-
пределы выносливости соответственно
при растяжении-сжатии и переменном
изгибе; n –
число вариантов сплавов и их состояний
для рассматриваемого класса материалов.
Предел выносливости при растяжении-сжатии и средняя квадратическая ошибка оценивания с учетом (2.16) вычисляется по формулам
(2.17)
и
(2.18)
С учетом уравнений (2.6)...(2.10), (2.13)...(2.15) получим
а)
для углеродистых сталей сплавов (
=0,919)
; 
; (2.19)
б)
для легированных сталей сплавов (
=0,914)
; 
; (2.20)
в)
для общей совокупностей сталей сплавов
(
=0,916)
; 
; (2.21)
г)
для деформируемых алюминиевых сплавов
(
=0,954)
; 
; (2.22)
д)
для деформированных титановых сплавов
(
=0,829)
; 
; (2.23)
е) для чугунов в соответствии с ГОСТ 25.504-82
=0,65
(С. Ч.), 
=0,60
(К. Ч.), 
=0,70
(В. Ч.)
и пределы выносливости при растяжении-сжатии оцениваются с учетом формулы (2.17) и уравнений (2.13) – (2.15).
2.1.3. Оценка предела выносливости при переменном кручении
Как
установлено экспериментально, для
сталей и деформируемых алюминиевых
сплавов 
=
0.60, для деформируемых титановых сплавов 
=
0.514, 
=0.80,
0.85 и 0.75 для С.Ч., К.Ч. и В.Ч. соответственно,
где σ-1 и τ-1 —
пределы выносливости при переменном
изгибе и переменном кручении.
С учетом уравнений (2.6)-(2.10) и (2.13)-(2.15) предел выносливости при переменном кручении для указанных материалов вычисляется по формулам:
для деформируемых алюминиевых сплавов (Nб=107 циклов)
(2.24)
для деформируемых титановых сплавов (Nб=107 циклов)
(2.25)
для углеродистых сталей
(2.26)
для легированных сталей
(2.27)
для общей совокупности сталей
(2.28)
В
случае чугунов предел выносливости при
кручении оценивается с учетом приведенных
выше значений отношения 
и
уравнений (2.13)-(2.15).
2.2. Расчет характеристик сопротивления усталости конструкционных материалов при асимметричном цикле напряжений
При
расчетах на усталость деталей методом,
предложенным С.В. Серенсеном и Р.С.
Кинасошвили [7,8], для вычисления
коэффициента запаса прочности оценку
предельной амплитуды цикла напряжений
лабораторных гладких образцов производят
с применением коэффициента чувствительности
к асимметрии цикла напряжений 
и 
(см.
п. 1.4.29) на основании выражений
(2.29)
и
. (2.30)
В этом случае предел выносливости или предельное максимальное напряжение определяется по формулам
(2.31)
и
. (2.32)
Коэффициент чувствительности к асимметрии цикла напряжений определяют экспериментально, либо берут из справочной литературы. Применение формул (2.29), (2.30) равносильно использованию в качестве уравнения диаграммы предельных амплитуд линейной зависимости, что противоречит опытным данным.
В
авиационной практике для оценки
характеристик сопротивления усталости
при асимметричном цикле напряжений
широко используются уравнения И.А.Одинга
(1.10). Как показал дальнейший расчет,
коэффициент чувствительности к асимметрии
цикла при использовании уравнения
(1.10) для всех конструкционных материалов
принимает единое значение 
=0.41,
что находится в противоречии с
экспериментальными данными.