2.1.1. Оценка предела выносливости при переменном изгибе

Автором совместно с сотрудниками и студентами кафедры [5,6] на основании большого статистического материала рассмотрена и показана возможность достаточно надежной косвенной оценки предела выносливости  при симметричном изгибе образцов из алюминиевых и титановых деформируемых сплавов, углеродистых и легированных сталей на основании значений предела прочности  при статическом растяжении; рассмотрена точность подобной оценки и даны рекомендации по определению нижних (гарантированных) значений предела выносливости.

Анализу были подвергнуты 187 вариантов алюминиевых деформируемых сплавов в различном состоянии, 152 варианта титановых сплавов, 317 вариантов углеродистых и 393 варианта легированных сталей в различных состояниях (варианты режимов термической обработки, виды полуфабрикатов и т.д.). Предел прочности алюминиевых сплавов менялся в диапазоне от 100 до 650 МПа, титановых сплавов – от 350 до 1475 МПа, углеродистых сталей от 300 до 1700 МПа, легированных – от 450 до 2150 МПа. Анализу подверглись результаты испытаний, опубликованные в отечественной и зарубежной литературе.

В качестве уравнений линии регрессии рассматривались линейное (2.2) и степенное

,                            (2.3)

которое путем логарифмирования приводится к линейному

                                 (2.4)

где ,   ,  ,  .

Предел выносливости для алюминиевых и титановых сплавов соответствует базе 10⁷циклов.

Уравнения (2.3) и (2.4) в отличие от линейного уравнения (2.2) удовлетворяют граничным условиям (при ;  ).

Коэффициент корреляции r между пределом выносливости при симметричном изгибе  и пределом прочности при растяжении  в случае линейного соотношения (2.2) для всех рассматриваемых материалов находится в пределах 0.87...0.92 и отличается от выборочного значения корреляционного отношения [4] не более, чем на 2..3 величины среднего квадратического отклонения коэффициента корреляции S_r, что не дает достаточных оснований для отклонения линейного уровня (2.2), хотя оно и не удовлетворяет граничным условиям (при ; ). Значение оценок параметров уравнения (2.2), средней квадратической ошибки предела выносливости и относительной погрешности  на разных участках линии регрессии приведены в таблице 2.1. Относительная средняя квадратическая ошибка в средней части линии регрессии определяется величиной ; на границах линии регрессии ошибка находится с учетом её зависимости от уровня прочности материала.

 

Таблица 2.1 Параметры уравнения (2.2) и значения ошибки оценивания предела выносливости на разных участках линии регрессии

Материал	Уравнение линии регрессии*	, МПа	Относительная средняя квадратическая ошибка оценивания предела выносливости на разных участках линии регрессии.
			Начало	Середина	Конец
Алюминиевые сплавы		15	0,15	0,10	0,07
Титановые сплавы		65	0,26	0,17	0,11
Углеродистые стали		53	0,20	0,15	0,08
Легированные стали		53	0,18	0,11	0,07
*Здесь и далее напряжения  и  имеют размерность МПа.

 

Как показывают эксперименты и теоретические расчеты, средняя квадратическая ошибка в определении  путем непосредственных испытаний на усталость 8...10 образцов на кривую усталости, как того требует ГОСТ, составляет для алюминиевых сплавов 5...7 %, для сталей 5...10 % и титановых сплавов 7...15%. Поэтому погрешность косвенной оценки предела выносливости материалов средней и высокой прочности (середина и конец линии регрессии), превышающую в 1.5...2 раза ошибку при усталостных испытаниях, следует считать удовлетворительной. Однако, для материалов низкой прочности (начало линии регрессии) это различие достигает 2...3 раз.

При объединении двух классов сталей в единую совокупность (n = 668, = 290...2130 МПа, r = 0.906, =53.8 МПа) уравнение линии регрессии запишется как

,                          (2.5)

причем, относительная ошибка оценки предела выносливости на всём протяжении линии регрессии возрастает на 1.2%, что позволяет использовать уравнение (2.5) как для углеродистых сталей, так и для легированных.

При использовании в качестве уравнения линии регрессии выражения (2.4) коэффициент корреляции для рассматриваемых материалов увеличивается до 0.91...0.95, причем, расхождение с эмпирическим корреляционным отношением не превышает одной величины S_r, что говорит о практически полной адекватности линии регрессии экспериментальным данным [4].

Статистический анализ показал, что дисперсия экспериментальных значений вокруг линии регрессии (2.4) практически не зависит от уровня .

Эта закономерность равносильна постоянству средней квадратической ошибки оценивания предела выносливости по уравнению (2.3) для материалов малой, средней и высокой прочности.

Объединение углеродистых и легированных сталей в один статистический коллектив и в этом случае привел к увеличению погрешности оценивания предела выносливости лишь на несколько процентов, хотя параметры уравнения (2.4) статистически значимо отличаются друг от друга. Это говорит о высокой чувствительности применяемого метода статистического анализа.

Уравнения (2.3) для указанных материалов с численными значениями параметров и величиной относительной средней квадратической ошибки оценивания предела выносливости при переменном изгибе приведены ниже:

а) алюминиевые сплавы

,           (2.6)

б) титановые сплавы

,           (2.7)

в) углеродистые стали

,           (2.8)

г) легированные стали

,            (2.9)

д) объединенная совокупность сталей

,           (2.10)

Таким образом, нелинейное уравнение (2.3) имеет следующие преимущества перед линейным уравнением (2.2):

а) выполняются граничные условия;

б) увеличивается коэффициент корреляции r;

в) снижается ошибка оценивания предела выносливости для материалов средней и низкой прочности;

Поэтому для косвенной оценки предела выносливости при переменном изгибе для указанной группы конструкционных материалов следует пользоваться уравнениями (2.6)-(2.10).

Для дальнейшего повышения надежности получаемых косвенным образом характеристик сопротивления усталости целесообразно для практических целей использовать нижнюю (гарантированную) границу предела выносливости, которая определяется из выражения

,                   (2.11)

здесь  - нижняя (гарантированная) граница значения медианы предела выносливости, которая с вероятностью Р не ниже действительного значения медианы предела выносливости для рассматриваемого материала;  - оценка медианы предела выносливости по уравнениям (2.6)-(2.10); - относительная средняя квадратическая ошибка оценивания медианы предела выносливости по уравнениям (2.6)-(2.10); z_p — квантиль уровня Р нормального распределения (для Р=0.90, 0.95 и 0.99 значения z_p = 1.28, 1.64 и 2.33 соответственно [4]).

На рисунке 2.1-2.3 показаны зависимости оценки медианы предела выносливости при переменном изгибе и нижних гарантированных значений для вероятностей 0,90 и 0,99 от значений  при статическом растяжении образцов из деформируемых алюминиевых и титановых сплавов, а также из углеродистых и легированных сталей.

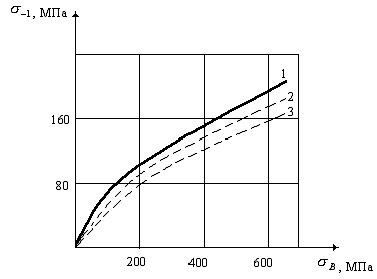
Рис.2.1. Зависимость медианы предела выносливости при переменном изгибе на базе 10⁷ циклов от предела прочности при статическом растяжении для деформируемых алюминиевых сплавов: 1- оценка медианы предела выносливости; 2,3- нижняя граница медианы для вероятностей Р=0,9 и 0,99 соответственно.

Рис.2.2. Зависимость медианы предела выносливости при переменном изгибе на базе 10⁷ циклов от предела прочности при статическом растяжении для деформируемых титановых сплавов: 1- оценка медианы предела выносливости; 2- нижняя граница медианы для вероятностей Р=0.90

Рис.2.3. Зависимость медианы предела выносливости при переменном изгибе от предела прочности при статическом растяжении для углеродистых (а) и легированных (б) сталей: 1-3 – то же, что на рис.2.1.

 

В соответствии с ГОСТ 25.504-82 оценка предела выносливости при переменном изгибе может производиться также по следующим нелинейным зависимостям:

а) стали (углеродистые и легированные)

                 (2.12)

б) высокопрочный чугун (В. Ч.)

                 (2.13)

в) ковкий чугун (К. Ч.)

                 (2.14)

г) серый чугун (С. Ч.)

                (2.15)