
Курнаев Введение в пучковую електронику 2008
.pdf
барьеров ширины |
dx, |
и |
|
проинтегрировать |
по |
ширине |
барьера |
|||||
(см. рис. 2.25): |
|
|
|
|
|
|
|
|
|
|
|
|
D = D D |
...D |
|
|
|
− |
4π x2 |
|
|
|
|
||
= exp |
h ∫ |
2m(W −W )dx = |
|
|||||||||
1 2 |
k |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
2 x2 |
|
|
|
|
|
|
|
|
= exp |
− |
|
|
2m(W −W )dx . |
|
|
|
|||||
= ∫ |
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
туннель- |
|||
|
|
|
|
|
|
|
|
ный эффект для элек- |
||||
|
|
|
|
|
|
|
|
тронной |
эмиссии. На |
|||
|
|
|
|
|
|
|
|
рис. |
2.26 |
изображена |
||
|
|
|
|
|
|
|
|
форма |
потенциального |
|||
|
|
|
|
|
|
|
|
барьера на границе ме- |
||||
|
|
|
|
|
|
|
|
талл – вакуум в присут- |
||||
|
|
|
|
|
|
|
|
ствии внешнего электри- |
||||
|
|
|
|
|
|
|
|
ческого поля. Зона 1 в |
||||
Рис. 2.26. Потенциальный барьер на гра- |
распределении |
электро- |
||||||||||
нов – зона «чистой» ав- |
||||||||||||
нице металл – вакуум в присутствии |
тоэлектронной |
эмиссии, |
||||||||||
внешнего электрического поля |
|
|
из нее |
электроны могут |
||||||||
выходить только за счет подбарьерного перехода. Зона 2 – зона автотермоэлектронной эмиссии, из этой зоны электроны, поднявшиеся на более высокий энергетический уровень за счет нагрева металла, проходят сквозь барьер меньшей толщины. Зона 3 – термоэлектронная эмиссия, вызванная эффектом Шоттки. Зона 4 – термоэлектронная эмиссия.
Вычислим прозрачность треугольного барьера (без учета сил электрического изображения). Заменим реальную форму барьера на треугольную (рис. 2.27). В вакууме распределение потенциала eV (x) = −eEx, x ≥ 0 . Коэффициент прозрачности барьера
|
|
2 |
x2 |
|
|
D = exp − |
∫ |
2m(eU (x) −Wx )dx , где нижняя граница интегри- |
|||
h |
|||||
|
|
|
x1 |
|
|
рования |
x1 = 0 , а верхняя определяется из равенства: Wx = −eEx2 , |
||||
|
|
|
|
211 |
|
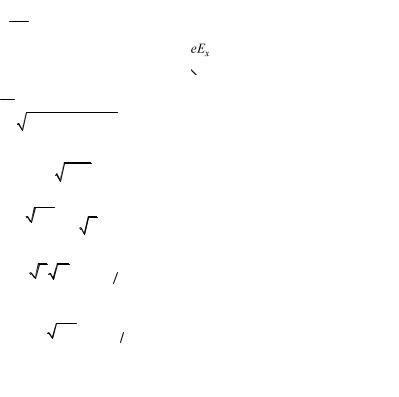
x2 = −WeEx . Введем обозначе-
ния: −eEx −Wx = η, dη= −eEdx .
Вычислим интеграл:
−WeEx
∫2m(−eEx −Wx )dx =
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
dη |
|
|
|
|
|
|
|
Рис. 2.27. Потенциальный барьер |
||||||||||||||||
= − ∫ |
|
|
2mη |
= |
|
|
|
на границе металл – вакуум в при- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
−Wx |
|
|
|
|
eE |
|
|
|
|
|
|
сутствии внешнего электрического |
||||||||||||||||||||
|
|
|
|
|
2m |
0 |
|
|
|
|
|
|
|
|
|
|
|
поля без учета сил электрического |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
изображения |
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
|
|
|
|
|
|
∫ |
|
|
ηdη |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
eE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
−Wx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
2 2 m |
(−W )3 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
тогда |
|
3eE |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
||||
|
|
4 |
|
|
|
2m |
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D = exp |
− |
|
|
|
|
|
|
|
|
|
(−Wx ) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
=eE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вычислим прозрачность потен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
циального барьера с учетом сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
электрического |
|
|
изображения |
Рис. 2.28. Потенциальный барьер |
||||||||||||||||||||||||||||||||
(рис. 2.28). В вакууме |
|
|
распре- |
на границе металл – вакуум в при- |
||||||||||||||||||||||||||||||||
деление |
потенциала |
|
eU (x) = |
сутствии внешнего электрического |
||||||||||||||||||||||||||||||||
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поля с учетом сил электрического |
||||||||||||||||||
= −eEx − |
|
x |
>0. |
|
|
|
|
|
|
|
|
|
изображения |
|
|
|
|
|
|
|||||||||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
||||||||||||
Точки |
x |
и |
x |
|
находим из равенства |
W |
x |
= −eEx − |
, получим |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение eEx |
2 |
+ Wx x + |
|
= 0, корни которого |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3E 1/2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−Wx ±Wx 1 |
− |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1,2 |
|
= |
|
|
|
|
|
|
x |
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2eE |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
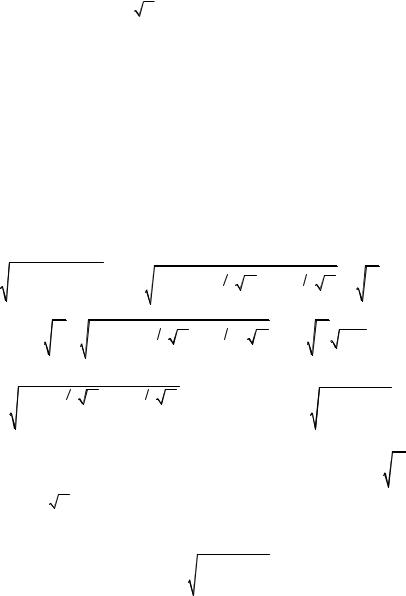
|
Учтем, что снижение потенциального барьера за счет эффекта |
||||||||||||||||||||||||||||
Шоттки |
|
(eϕa ) = e3/ 2 |
|
E |
много |
меньше |
|
энергии Wx , т.е. |
|||||||||||||||||||||
e3E = ( |
eϕa )2 <<Wx2 |
при |
|
Δϕa << ϕa , |
|
|
тогда в разложении |
||||||||||||||||||||||
1− |
e3E |
1/2 |
≈1− 1 e3E +... |
возьмем только первые два слагаемые: |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
W 2 |
2 W 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
−W |
+W |
|
− |
1 |
|
e3E |
|
|
|
|
|
|
|
e2 |
|
|
|
|
|||||
|
|
|
|
|
2 Wx |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x = |
|
|
x |
|
x |
|
|
= − |
1 |
|
|
|
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
2eE |
|
|
|
|
|
4 Wx |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
−W |
|
−W + |
1 e3E |
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 W |
|
|
W |
|
|
|
|
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
x |
|
x |
|
|
|
x |
|
|
|
|
|
|||||||||||
|
|
|
|
x = |
|
|
|
|
|
|
|
|
x |
= − |
|
+ |
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
2eE |
|
|
|
|
|
|
|
|
|
eE |
|
|
|
4 Wx |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для этих пределов интегрирования вычислим интеграл:
x |
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|||||
∫2 |
−eEx −Wx − |
dx = |
|
∫2 |
|
|
−Wx − 1 |
|
ξe3 2 |
|
|
E − |
1 1 e3 2 |
E 1 |
|
|
dξ = |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 ξ |
|
|
|
|
|
|
|
2 |
|
|
E |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
1 |
|
|
e |
ξ2 |
−W |
− |
1 |
ξe3 2 |
|
E − |
1 |
e3 2 |
1 |
E dξ = |
1 |
|
|
e |
−W |
× |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
E ξ∫ |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ξ |
|
|
|
|
2 |
|
|
E |
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ξ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
e3 2 |
E |
|
1 1 e3 2 |
|
E |
|
|
|
1 |
|
|
y |
(−Wx ) |
2 |
|
|
|
y |
|
|
|
|
1 |
|
||||||||||||||||||||||||||||||||
×∫ |
1+ |
|
|
ξ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
dξ= |
|
|
|
|
|
|
|
∫ |
1− |
|
|
ξ |
+ |
|
|
dξ. |
|||||||||||||||||||||||||||
|
2 |
|
W |
|
|
2 |
ξ |
W |
|
|
2 |
|
|
eE |
|
|
2 |
|
ξ |
|||||||||||||||||||||||||||||||||||||||||||
ξ1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Были |
введены |
|
|
|
|
|
|
следующие |
|
|
|
|
обозначения: |
|
|
x = |
1 |
ξ |
|
e |
, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
E |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y = − |
|
e3 / 2 |
E |
. Выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ(y) |
|
|
|
3 |
|
|
∫ |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
y |
|
|
1− |
|
|
|
|
ξ+ |
|
dξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.5) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
y |
|
|
|
|
|
|
|
|
2 |
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
213 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сии состоит в том, что при эмиссии катод не охлаждается, а наоборот, нагревается, так как эмитируются электроны с энергией Ex < EE без потерь энергии, и их место занимают электроны с бо-
лее высоких уровней, они то и разогревают катод.
При автоэлектронной эмиссии за счет «туннельного» эффекта эмитируются электроны, обладающие энергией, меньшей энергии Ферми: E < EF . Мощность поверхностного нагрева поверхности
за счет прихода более высокоэнергетичных электронов из объема металла: w = ( jT /e)(EF − E) . Таким образом, полевая эмиссия со-
провождается нагревом поверхности (эффект Ноттингема), в то время как термоэлектронная – охлаждением.
В зависимости от приложенного напряжения и свойств поверхности твердого тела возможны и другие виды электронной эмиссии из твердого тела, происходящие без его облучения электромагнитными квантами или частицами.
Взрывная эмиссия наблюдается при разрушении автоэлектронного острия собственным автоэмиссионным током за счет омического нагрева и эффекта Ноттингена при приложении импульсного поля выше некоторого критического (для вольфрама Eкр = = (6,5 ± 1) · 107 В/см). Взрыв острия (или микровыступа на плоском катоде) сопровождается образованием плазменного сгустка, быстрый уход из которого электронов приводит к образованию большого положительного объемного заряда. Это дополнительное поле усиливает эмиссионный ток до ~ 1000 A с одного острия ( j =
= 107 − 109 A/см2). Взрывной катод – эрозионный, потери атомов составляют ~ 10–2 на один эмитированный электрон. Однако после взрыва на соседних участках образуются новые удобные для подобного взрыва элементы микрорельефа. Поэтому после нескольких импульсов эмиссионные характеристики такого взрывного катода стабилизируются. Амплитуда прикладываемых импульсов напряжения составляет 104 − 107 В при длительности 10–7 − 10–9 с.
2.2.2. Неметаллические полевые эмиттеры электронов
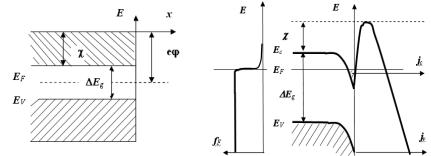
Плотность извлекаемого тока можно повысить, увеличив скорости электронов в твердом теле. Разогреть электроны, не расплавив кристаллическую решетку, можно в полупроводниках с высокой
217
Плотность тока «горячих» электронов в таких инжекционных катодах может достигать 100 А/см2.
Практически безинерционные катоды можно создать из диспергированных металлических пленок (ДМП) на диэлектрике. При приложении поля Е > 103 В/см вдоль такой структуры, состоящей из островков металла размерами ~ 10 нм на диэлектрической подложке, протекающий ток разогревает электронный газ в островке и туннелирующие от островка к островку через диэлектрические промежутки электроны становятся все более «горячими» по мере снижения на разность потенциалов между соседними островками барьера. Эмиссия горячих электронов с j = 1 − 10 A/см2 происходит из промежутков между островками.
Реализовать необходимые для полевой эмиссии высокие напряженности электрического поля можно в МДМ (металл-диэлектрик- металл) структурах. Для этого слой диэлектрика должен быть достаточно тонким (5 − 20 нм), поэтому разность потенциалов на металлических электродах в 5 − 20 В создает поля ~ 107 В/см. Ширина барьера при этом как в эффекте Шоттки резко уменьшается и электроны из металла попадают в зону проводимости диэлектрика, а затем в металлическую пленку. Эта положительная относительно базового металлического электрода пленка должна быть достаточно тонкой (10 − 20 нм), что обеспечит прохождение горячих электронов в ней без столкновений. Плотность тока эмиссии МДМ-структур может составлять до 10 А/см2, а зависимость от приложенного напряжения подчиняется закону Фаулера Нордгейма. В качестве эмиссионных МДМ-структур используются Al- Al2O3-Al, Al-Al2O3-Au, Au-BN-Au, Be-BeO-Au и др.
Следует отметить, что спонтанное образование описанных выше структур возможно в плазменных установках при распылении и переосаждении материалов в результате попадания частиц плазмы на обращенные к ней элементы, вследствие того, что в остаточном газе, как правило, всегда присутствует кислород. Так как на границе плазма-стенка всегда присутствует вытягивающее электроны поле, а пристеночная разность потенциалов определяется в том числе эмиссионными свойствами поверхности, то генерация подобных структур может сильно повлиять на взаимодействие плазмы со стенкой.
219
Эмиссия электронов возможна и из чисто диэлектрических тонких слоев на поверхности металлических электродов (молтеровская эмисиия). Это явление достаточно широко распространено в плазменных установках, когда для электродов используют материалы, легко образующие оксиды (Al и его сплавы, например). Механизм возникновения эмиссии следующий: нанесенный из плазмы на поверхность диэлектрической пленки положительный заряд создает в тонком слое (≤ мкм) диэлектрика поле ~ 105−106 В/см, достаточное для ионизации донорных примесей в диэлектрике. Появление в результате этого положительного объемного заряда приводит к перераспределению поля с резким усилением напряженности на границе металла до 107 В/см, которого, в свою очередь, достаточно для туннелирования электронов из металла в свободную зону диэлектрика. Если на поверхности наступает равновесие между числом электронов, нейтрализующих поверхностный положительный заряд, и числом эмитированных электронов (эмиссия электрона соответствует приходу положительного заряда), то положительный заряд на поверхности поддерживается приходящими из металла электронами и наблюдается молтеровская эмиссия. Она может продолжаться длительное время и после выключения разряда и источника зарядки поверхности из плазмы. Причем длительность такой «спонтанной» эмиссии для пористых диэлектрических слоев, сопровождаемой свечением поверхности (за счет рекомбинации дырок и электронов), может достигать тысячи часов (при плотности тока эмиссии ~ 5 мА/см2).
Совершенно удивительно выглядит эмиссия с поверхности заряженных частиц (и нейтральных атомов), казалось бы, без внешних источников воздействия. Однако причины такой, на первый взгляд, спонтанной экзоэмисии вполне реальны и достаточно многочисленны.
Иногда эмиссия возникает после импульса разрядного тока (послеразрядная эмиссия). Эта эмиссия также связана с наличием на электродах оксидных пленок, в которых под действием сопровождавшего разряд электромагнитного излучения появляется заряд. Токи такой эмиссии очень малы (10–14−10–18 А/см2), но протекать они могут на протяжении длительного времени, так, для пористого
220
