та: tgβ = |
|
y1 |
= |
eE |
|
l |
|
= |
eUоткл |
|
l |
α =β , т.е. угол вылета сов- |
|
l |
m V |
2 |
2W |
|
d |
|
|
|
|
|
|
|
|
|
|
0 |
|
к0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
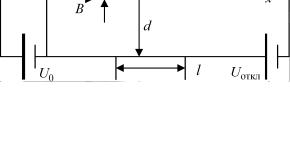
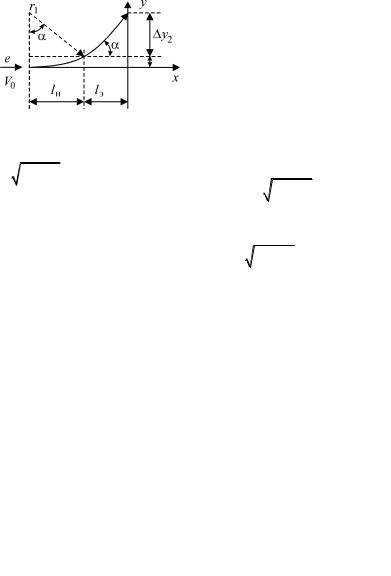
падает с углом β. Поперечное смещение на расстоянии x от центра системы определяется соотношением:
y = x tgα = eUоткл l x . 2Wк0 d
Рис. 3.9. Отклонение электронного пучка в поле плоского конденсатора
3.2.2. Фокусировка электронного пучка в однородном электрическом поле электростатического конденсатора
В поле плоского конденсатора можно не только отклонять, но и фокусировать пучки заряженных частиц. Благодаря различным значениям потенциала на верхней и нижней границах пучка (рис. 3.10), а значит, и различным скоростям частиц происходит фокусировка пучка. Такие системы используются в электроннолучевых трубках. Можно оценить фокусное расстояние (расстояние от центра системы до точки фокусировки). Распределение по-
тенциала в отклоняющей системе: U (y)=U0 +Uоткл dy . Тогда по-
|
|
|
|
|
d |
+ |
h |
тенциал |
в |
точках А и В: U A =U0 +Uоткл |
2 |
|
2 |
, UB =U0 + |
|
d |
|
|
d |
|
h |
|
|
|
|
− |
|
|
|
|
+Uоткл |
2 |
|
2 |
. Для малых углов отклонения: |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
311 |
|
|
|
|
α ≈ tg |
α = |
|
|
|
Uоткл |
|
|
|
l |
|
≈ (Uоткл |
<<U0 ) ≈ |
Uоткл |
|
l |
|
; |
|
|
|
|
|
|
|
d |
|
|
d |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2U |
|
|
|
|
|
|
|
U0 + |
2 |
Uоткл |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 ≈ tgα1 |
= |
|
|
|
|
|
Uоткл |
|
|
|
|
|
|
|
l |
= |
|
|
Uотклl |
|
|
|
|
; |
|
|
|
|
|
|
d |
+ |
|
h d |
2U0d +Uоткл (d + |
h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
U0 |
+Uоткл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α2 |
≈ tgα2 = |
|
|
|
|
|
|
|
Uотклl |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
2U0d +Uоткл (d − |
h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разность углов отклонения частиц на границах пучка:
Δα = α1 −α2 =Uотклl |
|
|
|
Uоткл (d + h −d + h) |
≈ |
(2U0d +Uоткл (d − h))(2U0d +Uоткл (d + h)) |
|
|
U 2 |
l |
h |
|
2α2 |
|
|
|
≈ |
откл |
|
|
≈ |
|
h. |
|
|
2U02d 2 |
l |
|
|
|
|
|
|
Рис. 3.10. Фокусировка электронного пучка в поле плоского конденсатора
Тогда фокусное расстояние можно оценить соотношением:
f = |
h ctg |
Δα |
= |
|
h |
≈ |
h |
= |
l |
. |
2 |
|
Δα |
Δα |
2α2 |
|
2 |
|
2tg |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Таким образом, с ростом угла отклонения уменьшается расстояние до точки фокусировки, это является причиной выпуклости экранов.
3.2.3. Отклонение в однородном магнитном поле, ограниченном в пространстве
|
|
|
|
|
|
|
|
Рассмотрим систему, в которой |
|
|
|
|
|
|
|
поперечное к движению пучка од- |
|
|
|
|
|
|
|
нородное магнитное поле сущест- |
|
|
|
|
|
|
|
вует в ограниченном пространстве |
|
|
|
|
|
|
|
протяженности lн (рис. 3.11). Маг- |
|
|
|
|
|
|
|
нитное |
поле |
|
будет разворачивать |
Рис. 3.11. Отклонение пучка |
|
|
|
частицы, отклонение в попереч- |
|
|
|
ном направлении в пределах дей- |
в поперечном магнитном поле |
|
|
|
|
ствия магнитного поля y1 = rл − |
|
|
|
|
|
|
|
− r2 |
−l2 , за пределами – |
y |
|
= l |
tgα = l |
|
|
|
|
lн |
|
|
. |
2 |
э |
r |
|
|
|
л |
н |
|
|
э |
|
|
|
2 |
−l2 |
Суммарное отклонение: |
|
|
|
|
|
|
|
|
|
|
л |
|
н |
|
|
|
|
|
l |
(l |
+ l |
|
) |
− r2 |
|
|
|
|
|
|
|
|
|
э |
|
|
|
y = y + y |
2 |
= r + |
|
н н |
|
|
|
|
|
л |
, |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
л |
|
|
|
r2 |
−l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V0 |
|
|
|
|
|
|
|
|
л |
|
|
н |
|
|
|
где r |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
eH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc
3.2.4. Фокусировка пучка в продольном однородном магнитном поле
В продольном однородном магнитном поле фокусировка происходит в силу того, что вышедшие из одной точки частицы после совершения одного оборота по ларморовской окружности возвращаются на исходную силовую линию магнитного поля (рис. 3.12).
Рис. 3.12. Фокусировка в однородном продольном магнитном поле
Рис. 3.13. Фокусировка пучка в поперечном магнитном поле
Проекция движения частиц на перпендикулярную к силовым линиям плоскость представляет собой пучок окружностей, имеющих общую точку. Если угол расходимости пучка α невелик, то фокусировка моноэнергетического пучка произойдет через один оборот на расстоянии l = tлVcosα ≈ 2πmVc/(eH), где tл = 2πmc/(eH) – период вращения по ларморовской окружности. Таким образом, расстояние до места фокусировки пучка зависит от скорости и массы частиц, и продольное однородное магнитное поле может быть использовано для энерго- и масс-сепарации частиц.
3.2.5. Фокусировка пучка в поперечном однородном магнитном поле энергоанализатора или массепаратора
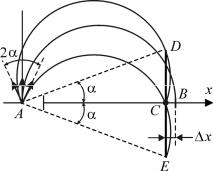
Благодаря зависимости радиуса вращения в магнитном поле от поперечной скорости V и массы m заряженной частицы возможно их разделение (сепарация) по энергиям и массам, а также фокусировка как в поперечном, так и в продольном однородном магнитном поле. В поперечном магнитном поле наиболее распространенной является схема с полукруговой фокусировкой (рис. 3.13). Выходящий из точечного источника А перпендикулярно силовым линиям пучок моноэнергетических частиц будет фокусироваться после полуоборота
на расстоянии AB = 2rл . Фо-
кусировка частиц, вылетевших под одинаковым углом α
кцентральной траектории
пучка, происходит из-за того, что круговые траектории частиц имеют одинаковые радиусы, и их траектории опираются на диаметры, расположенные под тем же углом α, что и касательные к траекториям в начальной точке:
AC = ADcosα = AE cosα, AD = AE = 2rл ,
|
где r = |
c |
2W m . Ширина щели, необходимая для прохожде- |
|
qH |
|
л |
к |
ния всего пучка, зависит от расходимости 2α входящего пучка: x = CB = AB − AC = 2rл (1−cosα).
Если известна масса и заряд, то можно определить энергию (энергоанализатор): m, q →Wк.
Если известна энергия и заряд, то можно определить массу (масс-сепаратора):Wк, q → m .
Если известна масса и энергия, то можно определить заряд (зарядоанализатор): m, Wк → q .
3.2.6.Отклонение и фокусировка ионного пучка
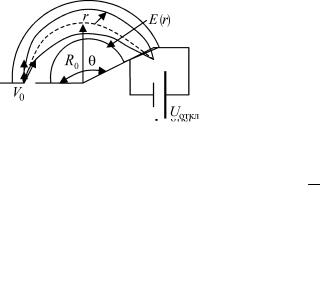
внеоднородном электрическом поле цилиндрического конденсатора (энергоанализатор)
Хорошую фокусировку позволяет получить цилиндрический конденсатор. Электрическое поле цилиндрического конденсатора обратно пропорционально расстоянию от центра системы: E(r) =
c/r, |
так как по теореме Гаусса: |
E 2π r l = Q , |
т.е. |
E = |
|
Q |
|
= |
c |
. |
2πlr |
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
|
c |
|
r |
Следовательно, |
уравнение |
|
для |
потенциала |
|
= − |
|
, |
тогда |
|
|
dr |
r |
|
|
dϕ |
|
dr |
|
Δϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
c = |
, где R , R |
– радиусы цилиндров (рис. 3.14). |
|
|
|
|
|
c |
|
r |
|
R |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, электрическое поле в цилиндрическом конденсато-
ре: E (r)= |
Uоткл |
, где U |
откл |
=U |
2 |
−U , U , U |
2 |
– потенциалы внут- |
|
|
r ln |
R2 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
реннего и внешнего цилиндра. Через узкую выходную щель будут «успешно» проходить только частицы, имеющие круговые траек-
|
mV |
2 |
= qE (R |
) |
тории и скорости, удовлетворяющие условию: |
0 |
|
|
R0 |
0 |
|
|
|
|
|

.. |
|
|
|
|
|
|
R2 |
|
|
R4 |
|
.. |
|
R2 |
(R + r)2 − R4 |
|
r +ω2 |
|
0 |
|
|
−ω2 |
|
0 |
|
= 0 или |
r +ω2 |
|
0 |
|
|
0 |
|
|
0 |
= 0 , в |
|
|
|
0 R0 + r |
0 (R + r)3 |
|
0 |
|
|
|
(R |
|
+ r)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
результате |
|
|
преобразований |
получим |
|
|
уравнение: |
.. |
|
|
|
R03rω02 |
2 |
r2 |
|
|
|
|
2 |
|
|
3 |
|
|
r + |
2 |
|
|
|
|
|
|
|
+ ω |
|
|
= 0 . Пренебрегая |
r |
|
|
и r |
|
, имеем гармо- |
(R |
+ r)3 |
(R + r)3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.. |
|
|
решение которого представляет |
нические колебания: r + 2ω2r = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
собой |
колебания |
около |
круговой траектории |
с |
полупериодом |
θ = |
T |
= |
|
π |
=127°17′, т.е. после поворота на этот угол пучок фоку- |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сируется на круговой траектории (фокусировка по Юзу и Рожанскому).
3.3.Элементы электронной оптики
3.3.1.Аналогия световой и электронной оптики
До сих пор рассматривалось движение отдельных частиц в электрическом и магнитном полях. Электронная оптика изучает законы распространения пучков заряженных частиц – электронов и ионов – в электрическом и магнитном полях. Пучки в электронной линейной оптике считаются достаточно редкими, так что электрические и магнитные микрополя от собственного объемного заряда пучка пренебрежимо малы по сравнению с макрополями отклоняющей системы. Уже первые эксперименты в конце XIX в. с катодными лучами показали, что законы распространения электронных лучей подобны законам распространения световых лучей в геометрической оптике. И дело вовсе не в том, что электроны мож-
но считать электронной волной. Комптоновские длины волн элек- |
|
h |
|
12,25 . |
трона λ = |
|
= |
|
A много меньше характерных размеров |
mV |
|
|
|
U [эВ] |
оптических систем, т.е. электроны можно считать частицей. Аналогия между движением заряженной частицы и распространением света более фундаментальна, и лежит она в существовании вариационного принципа. В геометрической световой оптике

a2
этот принцип имеет название принципа Ферма: δ ∫ndl = 0 , т.е.
a1
a2
δL = 0 , где L = ∫ndl – оптическая длина пути света; n = const –
a1
показатель преломления. Оптическая длина реального пути света должна быть минимальна (свет распространяется по такому пути, на котором он тратит наименьшее время). Свет распространяется прямолинейно. В механике вариационный принцип имеет вид:
|
t |
|
mV 2 |
|
Ze |
|
|
δ∫2 |
Ldt = 0 , где L = |
− Zeϕ+ |
A V ; A – векторный потенциал |
|
|
c |
|
t1 |
2 |
|
|
|
|
|
|
|
|
(H = rot A) ; L – функция Лагранжа. Вариация интеграла равна изменению этого интеграла при изменении обобщенный координат:
t2 |
|
. |
|
t2 |
|
. |
. |
|
t2 |
|
. |
|
δ∫ |
L qi ,qi dt =∫ |
L qi + δqi ,qi + δqi dt − ∫ |
L qi ,qi dt . |
t |
|
|
|
t |
|
|
|
|
t |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
То, что вариация равна нулю, говорит о том, что этот интеграл на действительной траектории имеет экстремум (рис. 3.16). Если H = 0 , то функция Лагранжа L =T −U , где T – кинетическая энер-
t2
гия, а U – потенциальная энергия. Величина ∫(T −U )dt = S назы-
t1
вается действием, а вариационный принцип называется принципом наименьшего действия: δS = 0 . Принцип наименьшего действия можно записать через обобщенный импульс, который равен
|
∂L |
|
Ze |
|
a2 |
|
|
|
|
δ∫ pdl =0 |
|
p = |
. |
= mV + |
|
A : |
– принцип Мопертюи для движе- |
c |
|
∂qi |
|
|
|
a1 |
|
ния материального тела в постоянном потенциальном поле аналогичен принципу Ферма геометрической оптики для световых лу-
a2
чей. При H = 0 δ∫Vdl =0. Покажем, что принцип Ферма эквива-
a1
лентен закону преломления геометрической оптики (рис. 3.17). Оптическая длина L = l1n1 +l2n2 ,
ее вариация:
δL = n1δl1 + n2δl2 ≈
≈ −n1δx sin α1 + n2δx sin α2 = 0,
откуда следует закон преломления геометрической оптики:
sin α1 |
= |
n2 |
. Получим аналогич- |
|
n |
sin α |
2 |
|
|
|
1 |
|
ный закон для электронной оптики.
Так как параллельная границе
|
раздела |
|
компонента скорости |
|
не |
меняется |
(рис. 3.18), |
то |
|
V1 sin α1 =V2 sin α2 . |
Следователь- |
|
но, |
sinα1 |
= |
V2 |
, или |
sin α1 |
= |
U2 |
|
|
|
|
|
|
V |
|
|
sinα |
2 |
|
|
sin α |
2 |
|
U |
1 |
|
|
|
|
1 |
|
|
|
|
|
(где U – ускоряющее напряжение) – закон преломления электронной оптики. Таким образом,
Рис. 3.16. Виртуальная и реальная траектории частиц
Рис. 3.17. Преломление света на границе двух сред
U – аналог показателя прелом- |
|
ления. |
|
Но у электронной оптики есть |
|
и существенные отличия от све- |
|
товой, они в основном состоят в |
|
следующем. |
Рис. 3.18. Преломление пучка |
1. Отдельные лучи в световой |
оптике независимы – электрон- |
заряженных частиц на границе |
ные лучи взаимодействуют друг с |
потенциалов |
другом. |
|
2. Показатель преломления для электронов всегда непрерывен, для света он, как правило, меняется скачком.
3.Диапазон изменения показателя преломления для электронов не ограничен, в оптике, как правило, n < 4.
4.Скорость электронов тем больше, чем больше показатель преломления, а скорость света наоборот.
5.Преломляющие поверхности для электронов, в отличие от световых лучей, не могут быть произвольными – распределение потенциалов всегда удовлетворяет уравнению Лапласа (линейная электронная оптика) или Пуассона (нелинейная электронная оптика).
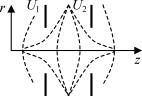
3.3.2.Потенциал аксиально-симметричного электростатического поля
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание преломляющих поверхно- |
|
|
|
|
|
|
|
|
|
стей в виде сеток достаточно сложно |
|
|
|
|
|
|
|
|
|
технически, поэтому часто используют |
|
|
|
|
|
|
|
|
|
диафрагмы с аксиально-симметричным |
|
|
|
|
|
|
|
|
|
распределением |
потенциала |
U (r, z) |
Рис. 3.19. Аксиально- |
|
|
(рис. 3.19). |
|
|
|
|
|
|
|
|
|
|
Так как U (−r, z) = U (r, z) , |
то в ре- |
симметричное поле |
|
|
зультате разложения U по r будут |
диафрагм |
|
|
|
|
|
|
только четные степени: |
|
|
|
|
|
|
|
|
|
|
|
|
U (r, z) = b |
(z) |
+b |
|
(z)r2 |
+b |
(z)r4 +... +b |
|
(z)r2k . |
|
|
0 |
|
2 |
|
|
|
|
|
4 |
|
2k |
|
|
Потенциал удовлетворяет уравнению Лапласа: |
|
|
|
|
|
|
|
|
|
∂2U |
+ |
|
1 ∂ |
U + |
∂2U = 0 . |
|
|
|
|
|
|
|
|
|
∂r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r ∂r |
|
|
|
|
|
∂2U = |
|
|
|
|
∂z2 |
|
|
|
|
С учетом |
|
2b |
(z) |
+ |
12b |
(z)r |
2 +30b |
(z)r4 |
+... ; |
|
|
|
|
∂r2 |
2 |
|
|
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∂ |
U = 2b |
(z) + 4b |
(z)r |
2 + 6b (z)r4 +...; |
|
|
|
|
|
|
|
|
r ∂r |
2 |
|
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2U |
= b0′′(z) + r2b2′′(z) + r4b4′′(z) +... ; |
|
|
|
|
|
|
∂z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение Лапласа перепишется в виде:
b0′′(z) + 4b2 (z) +(b2′′(z) +16b4 (z))r2 +(b4′′(z) +36b6 (z))r4 +... = 0.