дартного источника света – интегральную чувствительность. Глу-
бина выхода электронов из металлов составляет насколько атомных слоев, поэтому, теряя на своем пути часть энергии, фотоэлектроны на выходе из металлов имеют некоторое распределение по энергиям от нуля до максимального значения, определяемого по закону Эйнштейна. Распределение фотоэлектронов по энергиям можно определить экспериментально методом задерживающего потенциала. Для сбора на анод всех фотоэлектронов в опытах Лукирского и Прилежаева использовались катод в виде шара и анод в виде концентрической катоду сферы, через узкое отверстие которой на катод подавался луч света. Разность значений тока при двух задерживающих потенциалах -U и -(U + U) дает число фотоэлектронов, энергия которых при вылете с катода лежит в пределах от eU до e(U + U). Этот же метод можно использовать для определения красной границы фотоэффекта. Задерживающий потенциал, при котором фототок становится равным нулю, определяет разность между частотой ν кванта и граничной частотой фотоэффекта νгр для данного материала: U0 = h(ν - νгр)/e. Значения U0, определяемые для разных частот облучения ν, лежат на прямой, точка пересечения которой с осью абсцисс дает граничную частоту νгр.
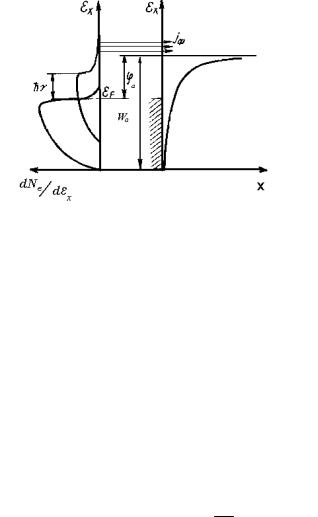
Основные закономерности ФЭЭ металлов хорошо описываются теорией Фаулера, согласно которой после поглощения в металле фотона его энергия переходит электронам проводимости, в результате чего электронный газ в металле около его поверхности состоит из смеси газов с нормальным (распределением Ферми) и возбужденным (сдвинутым на hν) распределением по энергиям (рис. 7.13). Для подсчета числа фотоэлектронов можно провести такое же интегрирование функции распределения, что и при подсчете плотности тока термоэмиссии, изменив нижний предел интегрирования с Wa на Wa - hν, тем самым включив в интегрирование электроны, которые приобретают недостающую для преодоления потенциального барьера энергию за счет поглощенных квантов. Так же, как и для термоэлектронов, необходимо учитывать вероятность прохождения барьера, так как часть электронов при движении из металла может быть отражена от поверхности раздела металл - вакуум.
Рис. 7.13. Фотоэмиссионный ток преодолевающих потенциальный барьер электронов из «хвоста» возмущенной функции распределения
Кроме этого, необходимо учесть вероятность поглощения фотона. Эта вероятность в общем случае зависит от энергии поглощающего электрона и энергии кванта. В теории Фаулера эта вероятность считается постоянной величиной, что, как оказалось, в интервале частот от νгр до 1.5νгр выполняется. В результате интегрирования плотность фототока определяется по формуле Фаулера:
B T 2 |
exp( |
hν −hνгр |
), |
ν ≤ν |
гр |
= eϕ |
a |
/ h |
|
|
|
|
1 |
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(7.29) |
jФ = |
|
|
(hν − hνгр )2 |
|
|
|
|
|
|
|
B T 2 |
( |
+ B ), |
ν >ν |
гр |
|
|
|
2 2 |
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
k T |
|
|
|
|
|
|
|
|
|
где B1, B2, B3 – постоянные коэффициенты, пропорциональные по-
стоянной Ричардсона A0. Зависимость jф( kThγ ) можно также пред-
ставить в виде рядов [32]. Из формулы Фаулера видно, что при Т ≈ 0 jф → 0 и νгр действительно является красной границей. При Т ≠ 0 не существует резкой границы фотоэффекта, фототок падает экспоненциально при ν < νгр, при ν > νгр плотность фототока пропорциональна квадрату частоты падающего излучения jФ ν 2.
262
Экспериментально положение νгр определяют по измеренной спектральной зависимости фототока при заданной температуре Т > 0. Эта зависимость откладывается на графике в координатах x = hν/kT и y = ln(jФ/T2). Полученная экспериментальная кривая соответствует зависимости:
ln( jФ/T2) = B + F((hν- hνгр)/kT) = B + F(x- hνгр/kT). |
(7.30) |
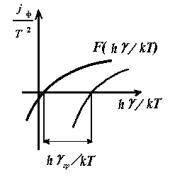
Экспериментальная кривая отличается от теоретической кривой функции Фаулера
F = F(hν/kT) сдвигом по оси y на константу B и по оси x на
hνгр/kT (рис.7.14). Именно определение сдвига по оси x
экспериментальной кривой для ее совмещения с теоретической кривой Фаулера позволяет найти граничную частоту νгр.
Рис. 7.14. Определение красной границы с помощью функции Фаулера
§48. Вторичная электронная эмиссия
Вторичная электрон-электронная эмиссия
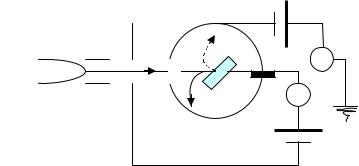
Эмиссия электронов с поверхности твердого тела, бомбардируемой потоком электронов, называется вторичной электронэлектронной эмиссией. Вторичная электронная эмиссия характеризуется количеством вторичных электронов на одну первичную частицу: γe = Ns/Np. Интегрально это количество равно отношению токов вторичных и первичных электронов Is/Ip. Схема экспериментального исследования энергетического распределения вторичных электронов методом задерживающего поля с использованием сферического коллектора показана на рис. 7.15.
I p
Рис. 7.15. Схема опыта по исследованию вторичной электрон-электронной эмиссии
Задерживающее поле прикладывается между мишенью и коллектором. Если потенциал коллектора Uk будет выше, чем на мишени, то на коллектор придет полный ток вторичной электронной эмиссии Is. Дифференцируя кривую задержки Uk(Is) находят энергетическое распределение электронов. Более точным методом определения скоростей вторичных электронов является использование дисперсионных электростатических энергоанализаторов, описанных в главе 5. Полученное экспериментальное энергетическое распределение (рис. 7.16) независимо от материала и энергии первичных электронов содержит два основных максимума. Первый в области малых энергий (<50 эВ) соответствует истинным вторичным электронам, которые выходят из твердого тела за счет поглощения энергии первичных электронов. Далеко не все электроны, получившие дополнительную энергию, добираются до поверхности, растрачивая энергию по пути на взаимодействие с ионами решетки и другими электронами. Преодолевшие потенциальный барьер истинные вторичные электроны на выходе имеют энергии, не зависящие от энергии первичных электронов. Работа выхода материала также не оказывает существенного влияния на эмиссию вторичных электронов, так как, во-первых, энергия первичных электронов, как правило, гораздо больше работы выхода, вовторых, эмиссия происходит не из поверхностных слоев, а из глубины металла, поэтому более важным является потеря энергии при движении электрона к поверхности. Второй, гораздо более узкий
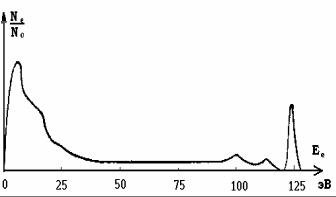
максимум находится в области высоких энергий и соответствует упруго отраженным первичным электронам, практически полностью сохранившим свою скорость после отражения (в силу малости отношения массы электрона к массе атомов мишени).
Рис. 7.16. Распределение вторичных электронов по энергиям
Область энергий между этими двумя максимумами соответствует неупруго отраженным вторичным электронам. Таким образом, энергетический спектр вторичных электронов состоит из широкого пика в области низких энергий с максимумом при Wmax (который принадлежит истинно-вторичным электронам, выходящим с глу-
бины 5 – 100 Ao от поверхности) и очень узкого пика отраженных от поверхности электронов в области высоких энергий с максимумом при энергии, равной энергии первичных электронов. Для характеристики истинной электрон-электронной эмиссии вводят коэффициент вторичной электронной эмиссии δe= Ns/Np , где Ns – число истинно вторичных электронов, Ns - число первичных электронов. Для характеристики эмиссии отраженных от поверхности первичных электронов используется коэффициент отражения ηe = (Ne+Nu)/Np, где Ne и Nu - упруго и неупруго отраженные электроны. Суммарный коэффициент вторичной электронной эмиссии γe = δe + ηe. Зависимость δe от энергии первичных электронов Wp можно найти по эмпирической формуле:
δe |
(Wp ) |
|
2 Wp |
|
|
|
|
|
|
= (2.72) |
|
− 2 |
Wp |
, |
(7.31) |
δ |
|
W |
exp |
W |
|
e max |
|
|
|
|
|
|
|
max |
|
|
max |
|
|
где δemax=  0.35eϕa , Wmax – значение и положение максимума.
0.35eϕa , Wmax – значение и положение максимума.
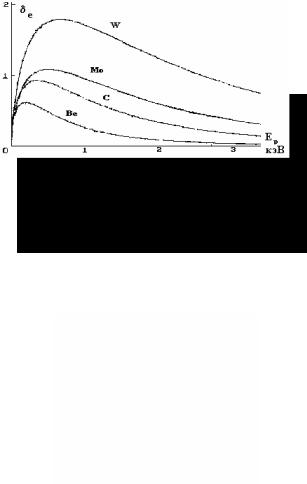
Рис. 7.17. Зависимость коэффициента истинной вторичной электронной эмиссии от энергии первичных электронов для W, Mo, C, Be
Рис. 7.18. Зависимость коэффициента отражения от энергии первичных электронов
Положение максимума зависимости коэффициента вторичной электронной эмиссии для разных материалов представлено в таблице 7.3. Рост δe с энергией первичных электронов сменяется спадом (рис. 7.17), так как при дальнейшем росте энергии первичных электронов образование вторичных происходит все глубже и глуб-
же и их выход становится все более затрудненным. Этим же объясняется существование сдвига максимума Wmax в энергетическом распределение вторичных электронов для материалов с высоким атомным числом (например, для вольфрама) в сторону низких энергий из-за снижения длины пробега первичных электронов в твердом теле (электронам, получившим энергию от первичных вблизи поверхности, легче выйти из твердого тела). Зависимость δe от угла падения первичных электронов α (угол с нормалью к поверхности) для α < 60о можно представить в виде:
δe (α) = δe (0) / cosβ α , |
(7.32) |
где β = 1.3 ÷1.5. Чем больше α, тем меньше глубина, которую нужно преодолеть вторичному электрону для выхода. Эмпирическая зависимость коэффициента отражения ηe для нормального падения электронов от энергии первичных электронов Ep (рис.7.18) и атомного номера z:
ηe (Ep , z) = Epm( z ) exp(C(z)) , |
(7.33) |
где m(z)=0.1382–0.9211z-0.5, C(z)=0.1904–0.2236lnz+0.1292ln2z–
0.01491ln3z -(формула Хунгера). Зависимость ηe от угла падения α:
ηe (α) = 0.891( |
ηe (0) |
)cosα (формула Дарлингтона). (7.34) |
|
|
|
|
0.891 |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 7.3. |
|
Al |
|
Be |
|
C (ал- |
С (гра- |
Cu |
Fe |
|
|
|
|
|
|
маз) |
фит) |
|
|
|
δemax |
1.0 |
0.5 |
|
2.8 |
1.0 |
1.3 |
1.3 |
|
Wmax[эВ] |
300 |
200 |
|
750 |
300 |
600 |
400 |
|
|
Mo |
|
Ni |
|
Ta |
Ti |
W |
|
|
δemax |
1.25 |
1.3 |
|
1.3 |
0.9 |
1.4 |
|
|
Wmax[эВ] |
375 |
550 |
|
600 |
280 |
650 |
|
|
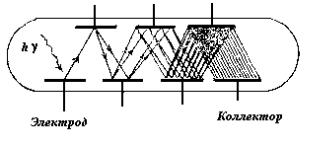
Наиболее распространенным применением вторичной электронной эмиссии являются электронные умножители, принцип действия которых показан на рис. 7.19. Максимально полное попадание вторичных электронов на последующий эмиттер может обеспечиваться магнитной или электрической фокусировкой. Между входным электродом и предпоследним прикладывается такая разность потенциалов, которая обеспечивает значение коэффициента вторичной электронной больше единицы между двумя соседними электродами. Именно при этом условии происходит размножение электронов с коэффициентом умножения для жалюзийного усилителя ~105. При регистрации фотонов используются специальные фотоэмисиионные катоды, а сам прибор помещают в отпаянную колбу (ФЭУ). Для регистрации корпускулярного излучения – ионов, электронов, быстрых атомов используют умножители открытого типа (ВЭУ-1, ВЭУ-2).
Разновидностью вторичного электронного умножителя является умножитель канального типа, который представляет собой изогнутый канал из специального полупроводящего стекла. Сам материал канала и его изогнутая форма обеспечивают более высокие коэффициенты эмиссии за счет наклонного попадания электронов на стенки с распределенным вдоль них потенциалом. Прикладываемая разность потенциалов (3-4 кВ), а коэффициент умножения составляет 106 – 108 (ВЭУ-4, ВЭУ-6). Для слабых плотностей потоков используют микроканальные пластины (МКП), что позволяет изготавливать позиционно чувствительные детекторы (и измерять, например, энергетический спектр частиц после плоскопараллельного электростатического дефлектора).
Рис. 7.19. Принцип действия вторичного электронного умножителя
Вторичная ионно-электронная эмиссия
При взаимодействии ионов с поверхностью твердого тела наблюдается эмиссия электронов, характеризуемая коэффициентом
ионно-электронной эмиссии: γi = ne/ni, где ne - число эмитированных электронов, ni - число ионов, упавших на ту же поверхность за то же время. Для однозарядных ионов γi = ne/ni = je/ji, при эмиссии под действием ионов зарядом Z γi = Zje/ji. Эмиссия электронов может происходить в результате двух процессов: первый процесс, связан с возбуждением электронов тела за счет потенциальной энергии электронов эмиттера в поле приходящего на поверхность тела иона – такую эмиссию называют потенциальной с коэффициентом эмиссии γп; второй процесс связан с возбуждением электронной системы тела кинетической энергией иона – в этом случае эмиссию называют кинетической с коэффициентом эмиссии γк. Если присутствуют оба процесса, то γi = γп + γк. Потенциальная ионноэлектронная эмиссия была открыта Пеннингом в 1928 г. При исследовании зависимости электронной эмиссии от энергии падающих ионов он обнаружил, что эмиссия остается и при очень малых, практически нулевых, энергиях ионов. Из этого можно было сделать вывод, что испускание электронов не связано с кинетической энергией ионов. В экспериментах было выявлено, что такая потенциальная ионно-электронная эмиссия происходит только для ионов, потенциал ионизации которых Vi в два раза больше работы выхода материала эмиттера ϕa:
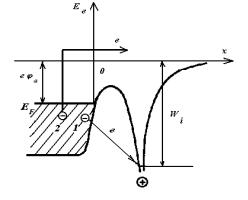
Рис. 7.20. Схема потенциальной ионно-электронной эмиссии
Это находит объяснение в модели оже-нейтрализации иона. Приближаясь к поверхности металла, ион изменяет своим полем поверхностный потенциальный барьер, понижая его. Один электрон, имея в металле энергию E1, совершает туннельный переход и нейтрализует ион (рис. 7.20). При этом выделяемая энергия Vi – E1 может быть передана второму электрону, имеющему в металле энергию E2. Для того чтобы второй электрон вышел из металла, его кинетическая энергия должна быть больше нуля: mv2/2=Vi – E1 – E2>0. С учетом того, что при низких температурах E1 и E2 меньше ϕa, Vi >2ϕa. Опыт показывает, что коэффициент γп линейно растет с увеличением разности Vi -2ϕa для различных пар мишень – ион. Для чистых поверхностей эту зависимость можно описать эмпирической формулой:
γп ≈ 0.016(Vi -2ϕa)[эВ]. |
(7.36) |
Коэффициент γп тем больше, чем больше заряд иона (кратность ионизации): γп(A+) < γп(A++) < γп(A+++). Для мишеней, поверхность ко-
торых достаточно чистая, γп практически не зависит от энергии падающих ионов Ep: dγп/dEp ≈ 0. При большой величине разности Vi - 2ϕa >> kBT коэффициент потенциальной ионно-электронной эмиссии не зависит от температуры поверхности мишени. При малой величине этой разности: Vi -2ϕa ≈ kBT термическое увеличение энергии электронов повышает вероятность эмиссии и γп растет с увеличением температуры, при этом потенциальная эмиссия воз-
можна и при Vi < 2ϕa.
При высоких энергиях падающих ионов кинетическая ионноэлектронная эмиссия преобладает над потенциальной. Экспериментально было обнаружено, что существует пороговое значение энергии первичных ионов, меньше которого коэффициент эмиссии γк ≈ 0. В припороговой области энергий ионов (Ep < 10 кэВ) коэффициент эмиссии пропорционален энергии: γк = С(Ep - (Ep)гр), где С = const. Для чистых металлов С ≤ 0.2 10-2 эВ-1. При более высоких энергиях γк Ep1/2 . При облучении монокристаллов коэффициент γк зависит от угла падения ионов на поверхность, причем эта зависимость носит периодический характер: положения максимумов совпадают с направлениями падающих ионов вдоль кристаллографи-