
- •Тема 1. Случайные события
- •2 Алгебра событий.
- •3 Определения вероятности события.
- •4 Элементы комбинаторики
- •1 Теоремы сложения вероятностей.
- •4 Формула полной вероятности. Формула вероятности гипотез.
- •Тема 2. Повторные независимые испытания
- •2 Наивероятнейшее число наступлений события в независимых испытаниях.
- •3 Локальная теорема Муавра-Лапласа.
- •4 Интегральная теорема Муавра-Лапласа. Пуассоновское приближение
- •Тема 3. Дискретные случайные величины
- •2 Закон распределения вероятностей дискретной случайной величины.
- •3 Математическое ожидание и его свойства.
- •4 Дисперсия дискретной случайной величины и ее свойства
- •5 Одинаково распределенные взаимно-независимые случайные величины
- •Тема 4. Непрерывные случайные величины
- •2)Дифференциальная функция (плотность распределения) непрерывной случайной величины и ее свойства.
- •Тема 5. Основные законы распределения случайных величин
- •1. Основные законы распределения дискретных случайных величин.
- •2) Равномерное распределение
- •Тема 6. Функции случайных величин и векторов
- •2) Композиция законов распределения
- •3) Специальные законы распределения
- •Тема 7. Многомерные случайные величины
- •2)Функции распределения многомерной случайной величины.
- •3)Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник.
- •4)Числовые характеристики системы двух случайных величин
- •Тема 8. Закон больших чисел
- •2)Неравенство и теорема Чебышева
- •3)Понятие о центральной предельной теореме
- •Часть II. Математическая статистика
- •Тема 10. Вариационные ряды распределения
- •1) Понятие и виды вариационных рядов распределения.
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Понятие и виды вариационных рядов распределения
- •2) Графическое изображение рядов распределения и связь между ними.
- •1) Средняя арифметическая и ее свойства.
- •2) Дисперсия ряда распределения и ее свойства. Среднее квадратическое отклонение.
- •3)Моменты ряда распределения и связь между ними
- •Тема 11. Выборочный метод
- •2)Статистические оценки выборочной совокупности и их свойства.
- •3) Точечные и интервальные оценки.
- •Тема 12. Проверка статистических гипотез
- •1)Понятие и виды статистических гипотез.
- •2)Статистический критерий проверки гипотез.
- •3)Уровень значимости. Мощность критерия.
- •2)Статистический критерий проверки гипотез
- •Тема 13. Дисперсионный анализ
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •1)Понятие и модели дисперсионного анализа.
- •2)Однофакторный дисперсионный анализ.
- •4.1.2.3. Двухфакторный дисперсионный анализ. Факторы а и в
- •Тема 14. Корреляционно-регрессионный анализ
- •1)Понятие корреляционной зависимости.
- •2) Оценка методом наименьших квадратов коэффициентов регрессии
- •Тема 15. Статистический анализ временных рядов
- •1)Понятие экономического временного ряда и его составляющие.
- •2)Тренд динамического ряда.
- •2)Тренд динамического ряда
Приложение Г – Конспект лекций
Тема 1. Случайные события
Лекция 1. Вопросы:
1 Предмет теории вероятностей.
2 Алгебра событий.
3 Определения вероятности события.
4 Элементы комбинаторики
1 Предмет теории вероятностей.
В процессе всей своей жизни человек часто сталкивается с событиями и явлениями, исход которых заранее не определен. Например, студент не знает, какие именно вопросы задаст экзаменатор, служащий – сколько времени у него займет дорога на работу завтра (через неделю), инвестор – окупятся ли его инвестиции, страховщик – причину и размер выплаты страхового вознаграждения и т. д. Тем не менее, в подобных ситуациях, связанных с неопределенностью, человеку необходимо принимать решение.
Теория вероятностей - это математическая дисциплина, изучающая закономерности, происходящие в массовых однородных случайных явлениях и процессах.
С возникновением теории вероятностей наука получила мощный аппарат исследования случайных явлений и процессов, до этого исследовались лишь детерминированные явления и опыты, в которых первоначальные условия однозначно позволяли определить исход. Между тем, случайные явления присутствуют во многих областях науки (биологии, генетике, агрономии, экономике, демографии, технике и т.д.), когда заранее невозможно предсказать результат опыта.
Исторически зарождение и развитие теории вероятностей связано с азартными играми, в которых требовалось обосновать то или иное решение..
Вероятность события – это число, всегда связанное с каким-либо пространством элементарных событий, природа которого не имеет значения. Понятие вероятности обычно строится на интуитивных соображениях (например, вероятность появления герба при подбрасывании симметричной монеты очевидно равна 1/2) и связано с понятием статистической устойчивости относительной частоты события при большом числе опытов. При подбрасывании монеты достаточно большое число раз относительная частота появлений герба будет колебаться около 0,5, следовательно, можно говорить, что вероятность появления герба равна 0,5. Наличие устойчивости относительной частоты появления события позволяет судить о вероятности, как об объективной характеристике события в данном опыте, имеющей вполне определенное значение, независимо от того, будут проводиться опыты или нет.
Целью современной теории вероятностей является выявление общих закономерностей и зависимостей, а также описание физических явлений с помощью абстрактных моделей.
. Математическая статистика - это раздел математики, в котором изучаются математические методы систематизации, обработки, анализа и представления статистических данных для научных и практических выводов.
Математическая статистика использует математический аппарат и выводы теории вероятностей. Связующим звеном между теорией вероятностей и математической статистикой является закон больших чисел и так называемые предельные теоремы
2 Алгебра событий.
Одним из основных понятий теории вероятностей является опыт. Под опытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события (факты). Событие это возможный результат опыта или испытания.
Простейшие неразложимые результаты опыта называются элементарными событиями (i), а вся совокупность элементарных событий называется пространством элементарных событий={i}. С каждым опытом связано свое пространство элементарных событий.
Любое конечное или счетное подмножество называется событием. Различают три типа событий:
достоверные (),
случайные,
невозможные (Ø или
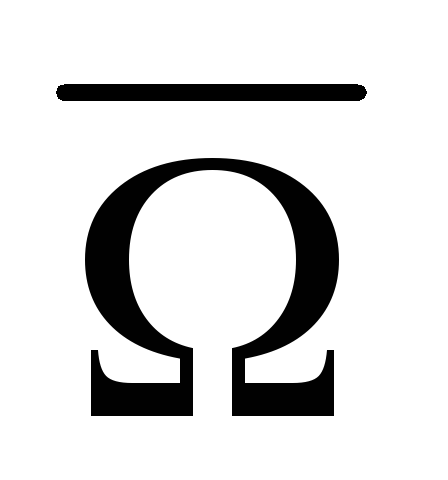 ).
).
События обычно обозначают первыми прописными буквами латинского алфавита: А, В, С,…. Событие называется достоверным, если в результате опыта оно обязательно произойдет. Событие называется невозможным, если оно не может произойти в данном опыте. Случайным называется событие, которое в данном опыте может произойти, а может и не произойти..
События А и В несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае - совместны. Например, при одном подбрасывании монеты не могут одновременно появиться герб и решетка.
Элементы последовательности событий А1, А2,…,Аnпопарно несовместны, если любые два из них несовместны. Например, при подбрасывании игральной кости никакие два элементарных исхода (появление цифр 1, 2, 3, 4, 5, 6) не могут произойти одновременно. Несколько событий равновозможные, если ни одно из них не является более возможным, чем другие. Несколько событий называются единственно возможными, если в результате испытания произойдет хотя бы одно из них.
События
А1,…,Аnобразуют
полную группу, если в результате опыта
кроме этих событий ничего не может
произойти, т. е. они являются несовместными
и единственно возможными. Обычноизображают на плоскости в виде некоторой
области, аiв виде точек этой области, устанавливая,
таким образом, соответствие между
событиями и точечными множествами. Над
событиями вводятся операции, совпадающие
с операциями над множествами: сумма,
произведение, отрицание. 1. Суммой
событий А и В называется такое третье
событие А+В (или АВ),
которое заключается в наступлении хотя
бы одного из событий или А, или В. 2.
Произведением двух событий А и В
называется такое третье событие АВ (или
![]() ),
которое заключается в наступлении
событий А и В одновременно. Если события
А и В несовместны, то АВ=. 3. Отрицанием события А называется
событие
),
которое заключается в наступлении
событий А и В одновременно. Если события
А и В несовместны, то АВ=. 3. Отрицанием события А называется
событие![]() (не А), заключающееся в не наступлении
события А (А+
(не А), заключающееся в не наступлении
события А (А+![]() =,
А
=,
А![]() =
=![]() ).
Причем, если в результате опыта может
произойти событие А, то может произойти
и обратное ему событие
).
Причем, если в результате опыта может
произойти событие А, то может произойти
и обратное ему событие![]() .
.
Если наступление события А приводит к наступлению события В и наоборот (наступление В влечет наступление А), то события А и В равны (А=В).
Пусть S– множество всех подмножеств, для которого выполняются следующие свойства:
если
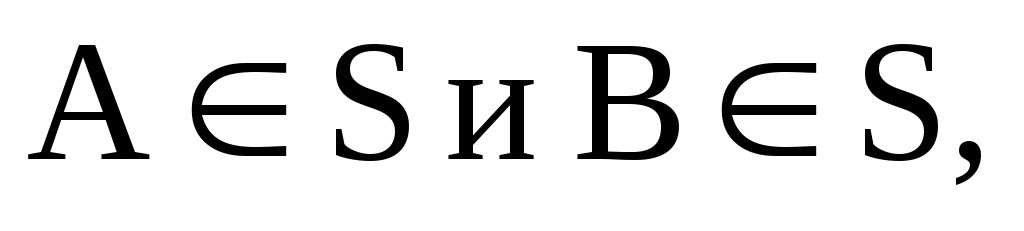 то
то
если
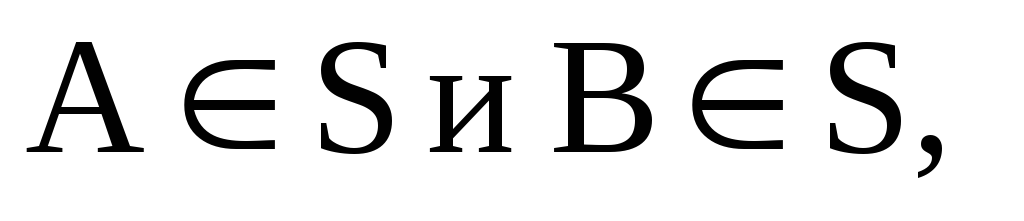 то
то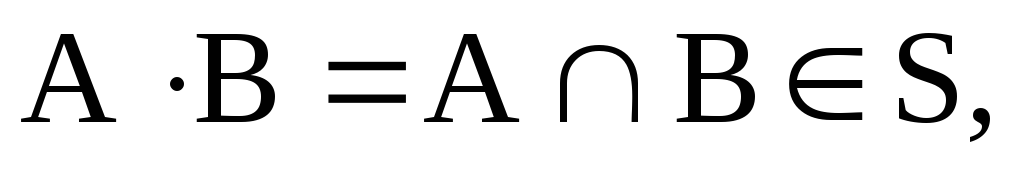
если
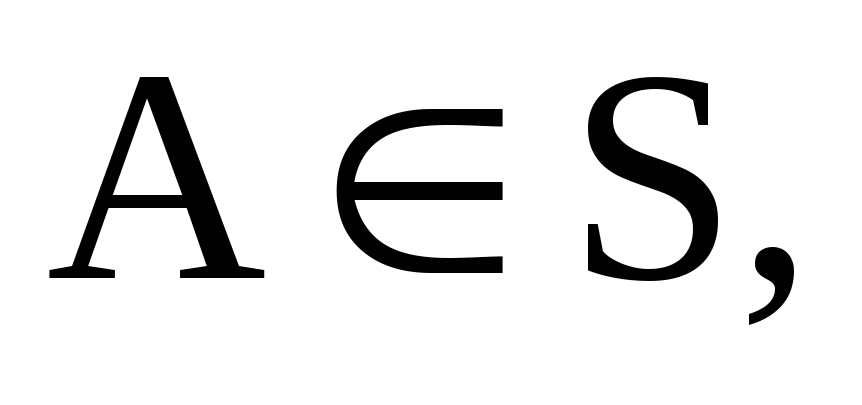 то
то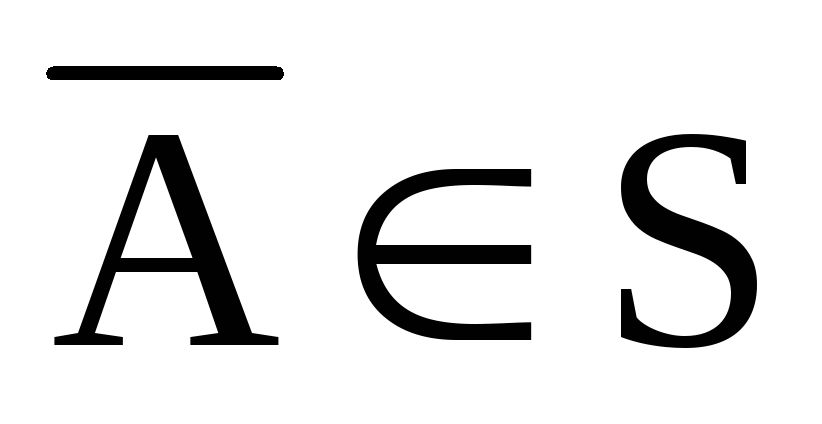 ,
,
тогда множество Sназывается алгеброй событий.
