§3. Условия перпендикулярности и компланарности вектора и плоскости, заданной общим уравнением

Теорема 1.В декартовой прямоугольной системе координатвекторперпендикулярен плоскости, заданной уравнением.

Доказательство.Возьмем на плоскости, заданной общим уравнениемотносительно декартовой прямоугольной системы координат, две произвольные различные точкиМ₁(х₁,у₁,z₁) иМ₂(х₂,у₂,z₂). Тогда

,,

откуда

или

. (3.8)

Следовательно, если вектор перпендикулярен любой прямой, лежащей на данной плоскости, то он перпендикулярен и самой плоскости.

При условии, что М₁(х₁,у₁,z₁) =М₀(х₀,у₀,z₀), аМ₂(х₂,у₂,z₂) =М(х,у,z), уравнение (3.8) называетсявекторным уравнением плоскости, проходящей через точкуМ₀(х₀,у₀,z₀) и перпендикулярной к вектору, который называетсяглавнымилинормальным вектором плоскости.

Теорема 2.Пусть относительно декартовой прямоугольной системы координат в пространстве заданы вектори плоскость общим уравнением

. (3.9)

Тогда необходимое и достаточное условие компланарности вектора и данной плоскости имеет вид

.

Доказательство. Необходимость.Если векторкомпланарен плоскости, заданной общим уравнением (3.9), то он перпендикулярен главному векторуплоскости и, следовательно,

.

Достаточность.Если, то векторперпендикулярен вектору, а значит он компланарен плоскости, для которой векторявляется главным, т.е. заданной уравнением (3.9).

Из теорем 1 и 2 следует, что если А= 0, то уравнение (3.9) принимает вид

(3.10)

и определяет плоскость, нормальный вектор которой перпендикулярен к осиОх. Следовательно, уравнение (3.10) определяет плоскость, параллельную или проходящую через осьОх.

Аналогично условия В = 0 иС = 0 являются необходимыми и достаточными условиями того, что плоскость соответственно параллельна или проходит через осьОу, параллельна или проходит через осьОz.

Отсюда следует, что плоскость параллельна или совпадает с одной из координатных плоскостей тогда и только тогда, когда в общем ее уравнении (3.9) два из коэффициентов А, В, С обращаются в нуль.

Таким образом, уравнения , илии только уравнения первой степени такого вида в случаеявляются уравнениями плоскостей, параллельных координатным, а в случаеуравнениями координатных плоскостей соответственноуОz, хОz, хОу.

Отметим также, что необходимым и достаточным условием того, что плоскость, заданная общим уравнением (3.9), проходит через начало координат, является равенство D = 0, так как в этом случае этому уравнению удовлетворяет точка О (0, 0, 0).

§4. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой

Пусть даны три точки: М₁(х₁,у₁,z₁),М₂(х₂,у₂,z₂) иМ₃(х₃,у₃,z₃), не лежащие на одной прямой. Эти точки однозначно определяют плоскость, проходящую через них. Найдем уравнение этой плоскости.

Возьмем произвольную точку пространства М(х,у,z) и построим векторы

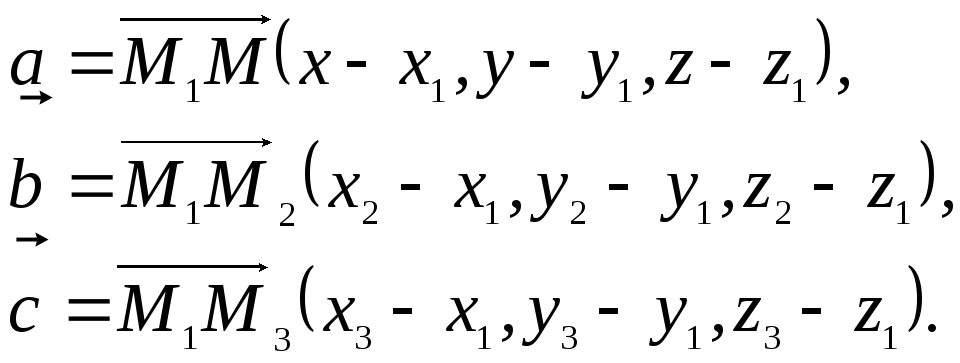
Точка М(х,у,z) принадлежит искомой плоскости тогда и только тогда, когда векторылежат в этой плоскости, т.е. когда они компланарны следовательно, смешанное произведение этих векторов равно нулю:

Запишем это произведение через координаты перемножаемых векторов. Имеем

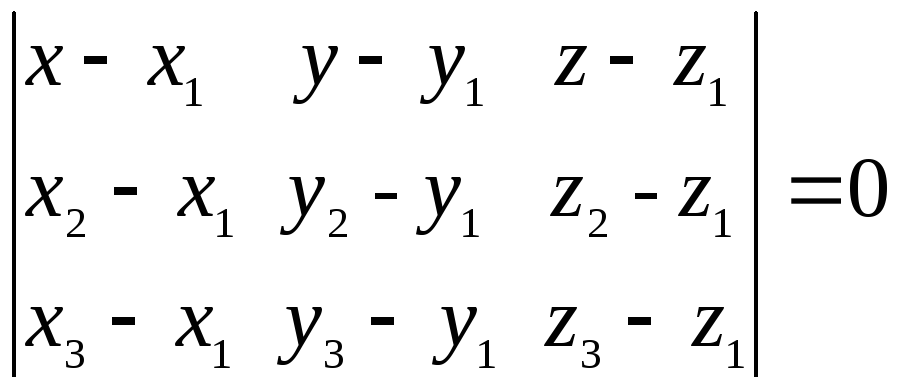(3.11)

Уравнение (3.11) называется уравнением плоскости, проходящей через три данные точки.