§10. Расстояние от точки до прямой

Если прямая задана нормальным уравнением (2.19) относительно декартовой прямоугольной системы координат, то расстояние dот точкидо этой прямой равно абсолютной величине результата подстановки координат точкиР₁в левую часть нормального уравнения

.

Доказательство.Пусть– произвольная точка данной прямой (рис.3.5). Так как векторявляется нормальным к данной прямой (система координат декартова прямоугольная), то (рис.3.5)

так как и значит.

Замечание. Иногда расстоянию от точки до прямой приписывают знак; называют такое расстояниеотклонениеми полагают

. (2.20)

Прямая делит плоскость на две полуплоскости. Для точек, находящихся в полуплоскости, содержащей начало координат О (0,0)и эту полуплоскость называютотрицательной. Для полуплоскости, не содержащей начало координат,и эту полуплоскость называютположительной.

§11. Угол между двумя прямыми; условия коллинеарности и перпендикулярности двух прямых

Пусть две прямые заданы относительно декартовой прямоугольной системы координат общими уравнениями

(2.21)

Тогда угол между векторами иравен одному из углов, образованных этими прямыми, а значит, косинусы и синусы этих углов будут вычисляться по формулам

; (2.22)

. (2.23)

Из формулы (2.22) находим необходимое и достаточное условие перпендикулярности двух прямых

, (2.24)

а из (2.23) – условие коллинеарности двух прямых:

(см. §8). (2.25)

Если данные прямые не взаимно перпендикулярны, то

(2.26)

Определим, какой вид примет формула (2.26), если прямые (2.21) будут заданы уравнениями с угловыми коэффициентами и. Для этого преобразуем формулу (2.26) и подставим в нее значенияk₁иk₂:

. (2.27)

Отсюда находим необходимые и достаточные условия перпендикулярности и коллинеарности двух прямых с угловыми коэффициентами:

или– условие перпендикулярности;

– условие коллинеарности.

Глава 3

ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ

§1. УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ

ТОЧКУ КОМПЛАНАРНО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ

Теорема. В декартовой прямоугольной системе координатx, y, zуравнение плоскостиP, проходящей через точку, компланарной двум неколлинеарным векторами, имеет вид

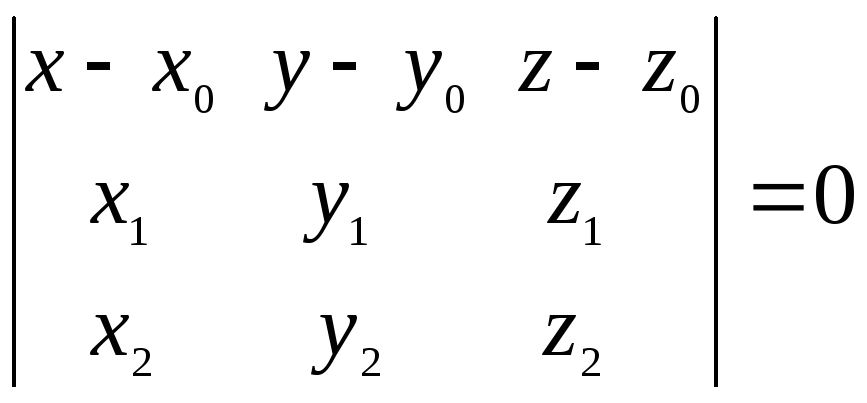(3.1)

Доказательство. Пусть– произвольная точка пространства. Точкалежит на плоскостиРтогда и только тогда, когда векторы,икомпланарны. Необходимое и достаточное условие компланарности этих векторов имеет вид (кн.2, гл.6, §3, п.3.2):

.

§2. ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Покажем, что алгебраической поверхностью первого порядка является плоскость. Для этого докажем следующие теоремы.

Теорема 1.Плоскость в прямоугольной декартовой системе координат определяется общим уравнением первой степени относительно текущих координат.

Доказательство. Фиксируем на плоскостиРпроизвольную точкуи возьмем два неколлинеарных вектораи, каждый из которых коллинеарен плоскостиР. Тогда на основании предыдущего параграфа уравнение плоскостиРможно записать в виде (3.1) или

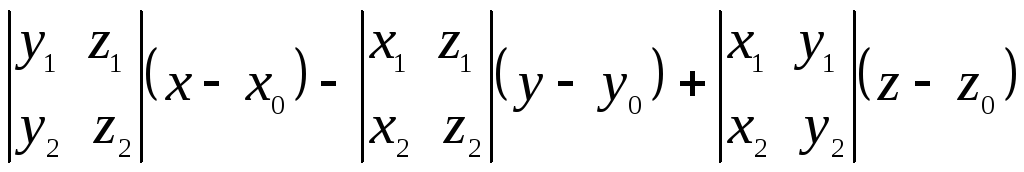. (3.2)

Так как векторы инеколлинеарны, то по крайней мере один из определителей

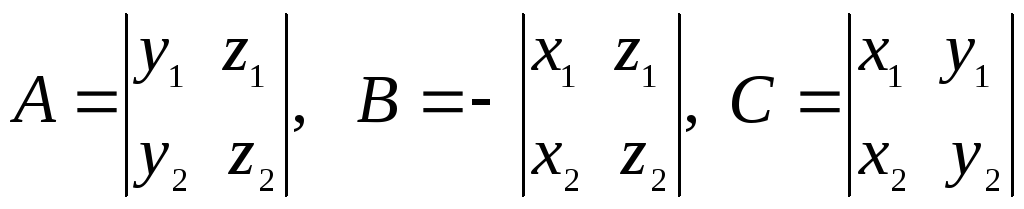
не равен нулю. Действительно, при равенстве нулю всех определителей имело бы место соотношение

,

а это означало бы, что векторы коллинеарны. Следовательно, уравнение (3.2) – уравнение первой степени относительно x, y, z.Если еще положить

,

то уравнение (3.2) примет вид

. (3.3)

Уравнение (3.3) называется общим уравнением плоскости.

Теорема2 (обратная). Общее уравнение первой степени

(3.4)

в прямоугольной декартовой системе координат x, y, z.Является уравнением плоскости.

Доказательство. Пустьx₀, y₀, z₀– какое-нибудь решение данного уравнения, т.е.

. (3.5)

Уравнение (3.4) будет эквивалентно уравнению, которое мы получим, вычитая почленно из уравнения (3.4) равенство (3.5):

. (3.6)

Одно из чисел не равно нулю; пусть, например,, тогда уравнение (3.6) эквивалентно уравнению

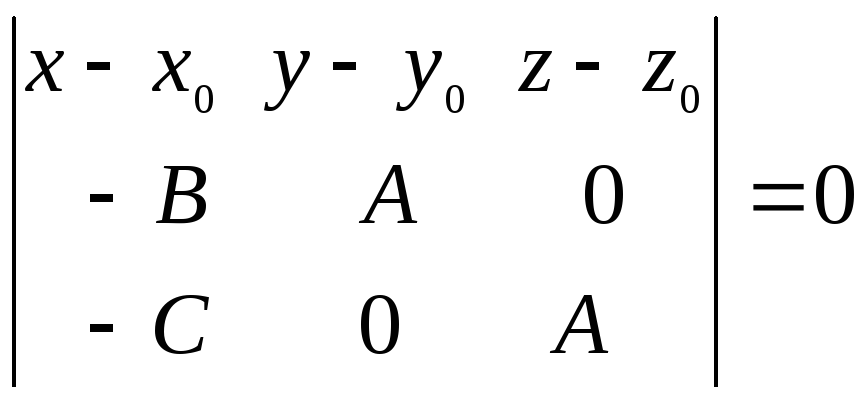. (3.7)

В самом деле, последнее уравнение после раскрытия определителя примет вид

,

или (так как )

.

Далее, векторы инеколлинеарны, поскольку один из определителей

не равен нулю (в силу условия не равен нулю первый определитель). Поэтому уравнение (3.7), а значит и данное уравнение (3.4) определяет (на основании предыдущей теоремы) плоскость, проходящую через точкукомпланарно двум не коллинеарным векторам (в случае):

и.

Аналогично доказывается, что данная плоскость (в случае ) компланарна векторами, неколлинеарным между собой, а в случае– векторами, которые также неколлинеарны.

Таким образом, каждая плоскость есть поверхность первого порядка, и, наоборот, каждая поверхность первого порядка есть плоскость.