§5. Угол между прямой и плоскостью. Условие перпендикулярности прямой и плоскости

Углом между прямой и плоскостью(если они не перпендикулярны) называется меньший из двух углов между этой прямой и ее ортогональной проекцией на эту плоскость. Если же прямая и плоскость перпендикулярны, то угол между ними считается равным.

Ортогональной проекцией прямой на плоскость называется прямая, образованная пересечением данной плоскости с плоскостью, проходящей через данную прямую перпендикулярно данной плоскости.

Пусть относительно декартовой прямоугольной системы координат задана плоскость общим уравнением

(4.8)

и прямая – каноническими уравнениями

. (4.9)

Обозначим угол между прямой и плоскостью через , а угол между нормальным вектором, перпендикулярным данной плоскости, и направляющим векторомданной прямой – через(рис.3.7).

Тогда (рис. 3.7, а) или(рис. 3.7, б), а. Но косинус угламежду векторамииравен

,

следовательно, синус угла между данной прямой и данной плоскостью определяется по формуле

.

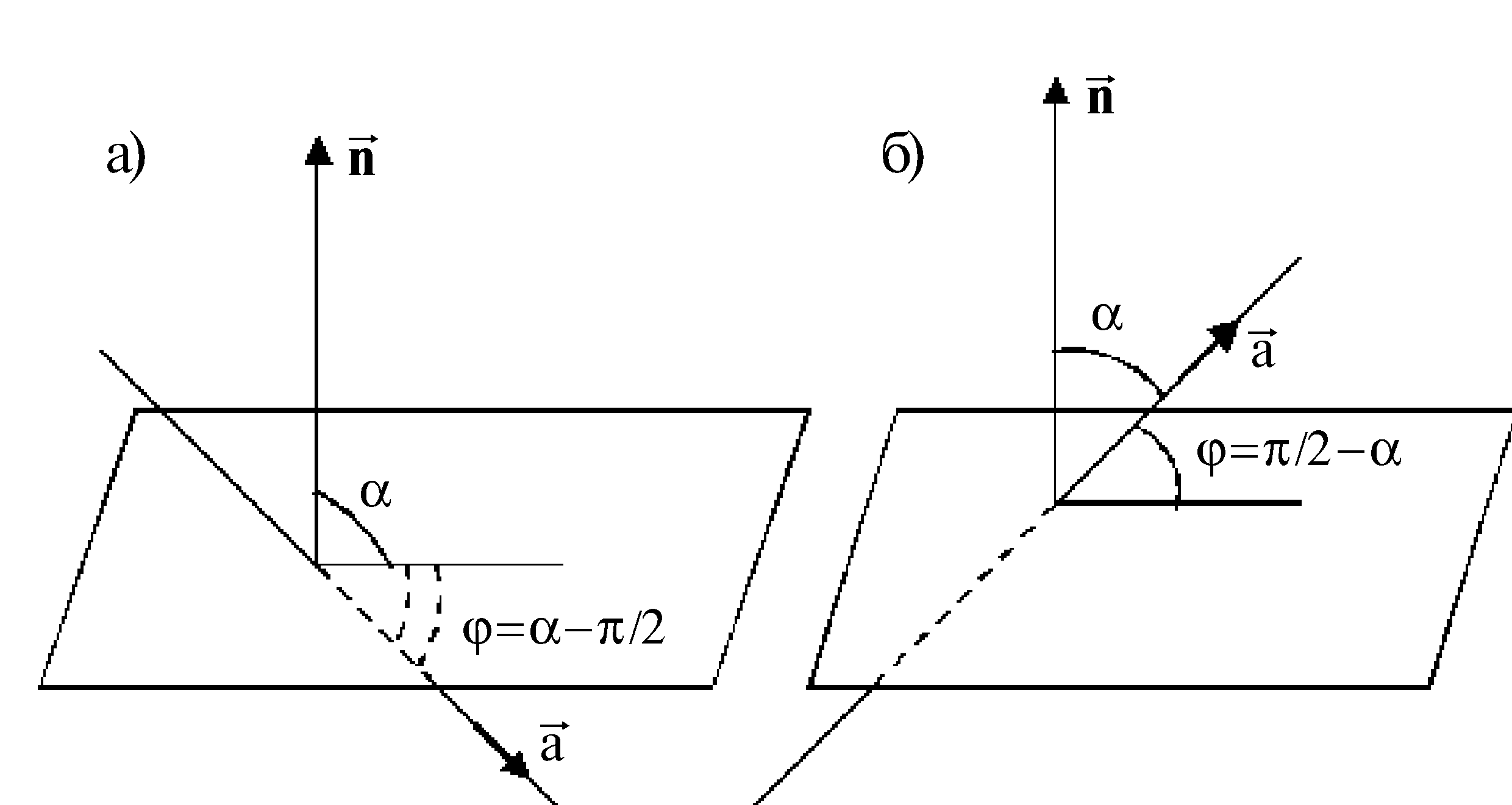
Рис. 3.7

Если прямая (4.9) перпендикулярна плоскости (4.8), то направляющий вектор прямой коллинеарен вектору, перпендикулярному данной плоскости. Поэтому координаты этих векторов пропорциональны, т.е. существует такое отличное от нуля число, что

,

или

.

Обратно, если выполнены эти соотношения, то векторы иколлинеарны, т.е. направляющий вектор данной прямой коллинеарен вектору, перпендикулярному данной плоскости, следовательно, данная прямая и плоскость взаимно перпендикулярны.

Итак, для того, чтобы прямая и плоскость, заданные относительно декартовой прямоугольной системы координат, были перпендикулярны, необходимо и достаточно, чтобы координаты направляющего вектора прямой были пропорциональны коэффициентам при x, y, zв уравнении плоскости.

§6. Кратчайшее расстояние между двумя скрещивающимися прямыми

Две прямые трехмерного пространства называются скрещивающимися, если они не пересекаются и не параллельны, т.е. не лежат в одной плоскости. Через две скрещивающиеся прямые можно провести только две параллельные между собой плоскости. Расстояние между этими плоскостями естькратчайшее расстояние между данными прямыми, – длина отрезка общего перпендикуляра к этим двум прямым, концы которого лежат на этих прямых.

Пусть две скрещивающиеся прямые заданы уравнениями (4.7) и требуется найти кратчайшее расстояние между ними d.

Векторное произведение направляющих векторов изаданных прямых, есть вектор, перпендикулярный к каждой из этих прямых:. Тогда кратчайшее расстояниеd между ними равно абсолютной величине проекции вектора

,

начало и конецкоторого лежат соответственно на первой и второй прямых, на прямую, параллельную вектору.

, или.

В координатах

.

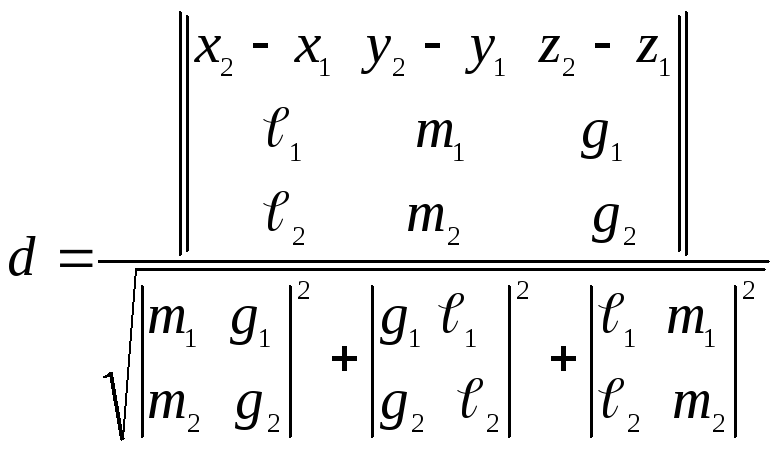Отметим, что эта формула верна и для двух пересекающихся прямых: числитель обратится в нудь, знаменатель отличен от нуля и мы получим .

Глава 5 линии и поверхности второго порядка

Напомним общее уравнение поверхности второго порядка (1.6):

. (5.1)

Если поверхность второго порядка пересечь какой-либо плоскостью (поверхностью первого порядка), то полученная в сечении линия представляет собой кривую второго порядка. Не нарушая общности рассуждений, в качестве секущей плоскости можно взять любую из координатных плоскостей.

Система уравнений, состоящая из уравнения (5.1) и одного из уравнений , определяет кривую второго порядка, расположенную соответственно в координатных плоскостяхyOz, xOz и xOy. В дальнейшем будем рассматривать линии второго порядка, расположенные в плоскостиxOy. Общее уравнение такой линии принимает вид (1.4)

, (5.2)

где , т.е. хотя бы одно из чиселне равно нулю.