§9. Приведение общего уравнения плоскости к нормальному виду

Пусть дано общее уравнение плоскости

. (3.21)

Умножим обе части этого уравнения на число :

. (3.22)

Уравнение (3.22) будет приведено к нормальному виду, если выполняются условия (3.20):

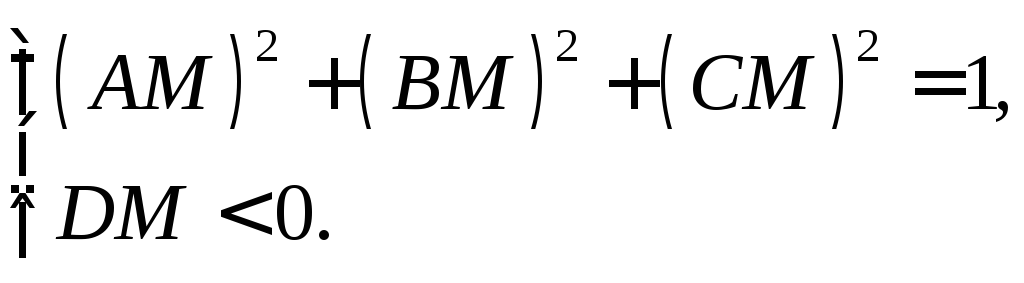
Решая эту систему относительно М, получаем

,

Число Мназываетсянормирующим множителем уравнения (3.21).

Если , то, и тогда

.

Если ,и тогда

.

Таким образом, знак нормирующего множителя противоположен знаку свободного члена уравнения плоскости. Если , тоМ можно взять с любым знаком.

Итак, чтобы преобразовать общее уравнение плоскости в нормальное, нужно обе части общего уравнения умножить на его нормирующий множитель.

§10. Расстояние от точки до плоскости

Теорема.Если плоскость задана нормальным уравнением

,

(где ) относительно декартовой прямоугольной системы координат, то расстояниеdот точкидо этой плоскости вычисляется по формуле

(или),

т.е. расстояние от точки до плоскости, заданной нормальным уравнением относительно декартовой прямоугольной системы координат, равно абсолютной величине результата подстановки координат данной точки в левую часть уравнения плоскости.

Доказательство. Из точкиМ₀на данную плоскость опустим перпендикуляр и рассмотрим вектор, где точка– основание перпендикуляра, принадлежит плоскости. Тогда(рис.3.6). Вектораиколлинеарны, поэтому, учитывая, что, имеем

.

Отсюда, принимая во внимание, что (точкаМ₁принадлежит плоскости), получаем

.

Если плоскость задана общим уравнением

,

то для того, чтобы найти расстояние dот точкидо плоскости, нужно сначала привести уравнение к нормальному виду, а затем найти абсолютное значение его левой части в точкеМ₀:

.

Замечание. Иногда расстоянию от точки до плоскости приписывают знак; называют такое расстояниеотклонениеми полагают

,

где – угол между коллинеарными векторамии.

Плоскость делит пространство на два полупространства. Для точек, находящихся в полупространстве, содержащем начало координат О (0, 0, 0) и. Это полупространство называютотрицательным. Для полупространства, не содержащего начало координат, и(рис.3.6). Это полупространство называютположительным.

Глава 4 прямая и плоскость в трехмерном пространстве

§1. Уравнения прямой в трехмерном пространстве

Прямая линия в трехмерном пространстве может быть задана различными способами: точкой и направлением, пересечением двух плоскостей, двумя точками и др.

1.1. Канонические и параметрические уравнения прямой

В декартовой системе координат уравнения прямой, проходящей через точку и имеющий направляющий вектор, будут

. (4.1)

Эти уравнения называют каноническими уравнениями прямой в трехмерном пространстве или в параметрической форме

. (4.2)

Действительно, пусть – произвольная точка; она лежит на прямой, проходящей через точкуМ₀, коллинеарной векторутогда и только тогда, когда векторыиколлинеарны, т.е. тогда и только тогда, когда координаты этих векторов пропорциональны:

.

Так как , то необходимое и достаточное условие коллинеарности векторовиможно записать еще и так:

(вектора пропорциональны),

или

, (4.3)

откуда сразу получаются уравнения (4.2).

В уравнениях (4.1) одно или два числа из чисел могут быть равными нулю. Одновременно все три числане могут обращаться в нуль, так как. Будем считать, что если один из знаменателей уравнения (4.1) обращается в нуль, то соответствующий числитель обращается также в нуль. Например, отношениеозначает, чтоили, т.е. оно определяет плоскость, перпендикулярную к осиОх.

Если , то направляющий векторперпендикулярен к оси абсцисс. Тогда уравнения

определяют прямую, перпендикулярную к оси Ох.

Аналогично уравнения, в которых или, определяют соответственно прямые, перпендикулярные к осямOy и Oz. Если, или, или, то уравнения (4.1) определяют прямые, параллельные соответственно координатным осямOz, Oy, Ox..

Канонические и параметрические уравнения прямой в трехмерном пространстве можно записать и в векторной форме. Для этого введем радиус-вектор точкии радиус-векторточки. Тогда, в силу коллинеарности векторови, их векторное произведение равно нуль-вектору

(4.4)

а уравнение (4.3) принимает вид

или. (4.5)

В координатном выражении уравнение (4.4) принимает вид уравнений (4.1) и поэтому оно называется каноническим уравнением прямой в векторной форме, а уравнение (4.5) – вид уравнений (4.2) и называетсяуравнением прямой в трехмерном пространстве в векторно-параметрической форме.