§3. Поверхности второго порядка, заданные каноническими уравненниями

3.1. Эллипсоид

Определение. Эллипсоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

. (5.25)

Будем считать, что Если на эллипсоиде (5.25) лежит точка, то на нем лежат и точки(с любым набором знаков плюс и минус). Отсюда следует, что для эллипсоида (5.25) начало координат является его центром симметрии и называетсяцентром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.

Если то эллипсоид (5.25) называетсятрехосным.

Если то эллипсоид (5.25) называетсявытянутым эллипсоидом вращения; он получается вращением эллипса вокруг его большой оси (рис.3.13, а).

Если то эллипсоид (5.25) называетсясжатым эллипсоидом вращения; он получается вращением эллипса вокруг его малой оси (рис.3.13, б).

Рис. 3.13

Если , то эллипсоид (5.25) является сферой радиусаа с центром в начале координат.

Вершинами трехосного эллипсоида называются точки пересечения эллипсоида с его главными осями. Трехосный эллипсоид имеет шесть вершин .

Из уравнения (5.52) следует, что .

Это означает, что эллипсоид (5.25) лежит внутри прямоугольного параллелепипеда с вершинами . Каждая грань этого параллелепипеда имеет с эллипсоидом (5.25) только одну общую точку – его вершину.

Плоскость хОу пересекает эллипсоид (5.25) по линии, выраженной уравнениями

или эквивалентной системой

. (5.26)

Аналогично плоскость yOz пересекает эллипсоид (5.25) по линии, уравнение которой

, (5.27)

а плоскость xOz по линии

. (5.28)

Линии (5.26), (5.27), (5.28) суть эллипсы. Эти эллипсы, т.е. сечения эллипсоида (5.25) его главными плоскостями, называются главными сечениями.

Рассмотрим сечения эллипсоида (5.25) плоскостями, параллельными какой-нибудь координатной плоскости, например, плоскостями, параллельными плоскости хОу, т.е. плоскостями, выражаемыми уравнением

,

где h – произвольное действительное число.

Уравнения линии сечения имеют вид

или

. (5.29)

Если , то первому уравнению этой системы не удовлетворяет ни одна пара действительных чиселх, у, т.е. система (5.29) не имеет действительных решений. Это означает, что плоскость прине пересекает эллипсоид (5.25).

При первое уравнение системы (5.29) имеет вид

,

откуда . Таким образом, плоскостивстречают эллипсоид (5.25) в его вершинах. Наконец, если, то систему уравнений, выражающих линию сечения, можно переписать так:

.

Эти уравнения являются уравнениями эллипса, лежащего в плоскости сечения ; центр этого эллипса – точка, оси симметрии параллельны осямОх и Оу, а полуоси равны

.

Рассмотренные сечения дают представление о форме эллипсоида. Такой способ исследования поверхности называется методом параллельных сечений; им мы будем пользоваться в дальнейшем при исследовании и других поверхностей.

3.2. Однополостный гиперболоид

Определение. Однополостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

. (5.30)

Будем считать . Также, как и в предыдущем разделе, доказывается, что для однополостного гиперболоида (5.30) начало координат является центром симметрии (центр), оси координат – осями симметрии (главные оси), а координатные плоскости – плоскостями симметрии (главные плоскости).

Если в уравнении (5.30) , то однополостный гиперболоид (5.30) называетсяоднополостным гиперболоидом вращения, так как может быть получен вращением гиперболы

вокруг ее мнимой оси (рис.3.14).

Вершинами однополостного гиперболоида называются точки пересечения гиперболоида с его главными осями. Гиперболоид в случае имеет четыре вершины.

Плоскость хОу пересекает однополостный гиперболоид (5.30) по эллипсу, выражаемыми уравнениями

,

Рис. 3.14

называемому горловым эллипсом однополостного гиперболоида. Плоскость yOz пересекает однополостный гиперболоид (5.30) по гиперболе, выражаемой уравнениями

,

а плоскость xOz– по гиперболе, выражаемой уравнениями

.

Рассмотрим сечения однополостного гиперболоида (5.30) плоскостями, параллельными координатной плоскости хОу, т.е. плоскостями.

Уравнения линии сечения будут

или

.

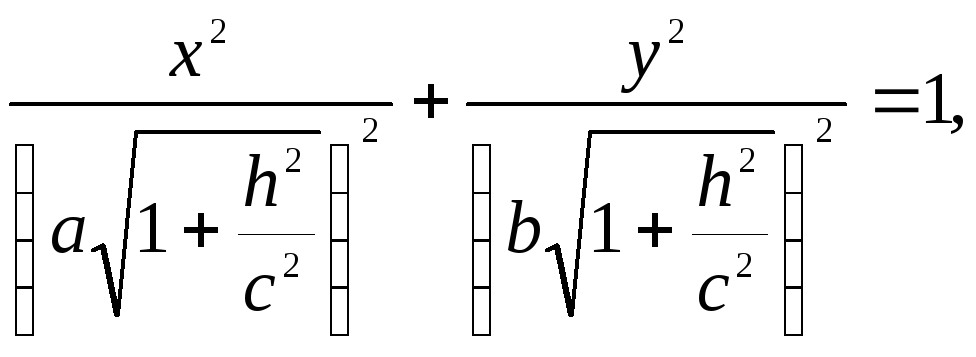
Этими уравнениями выражается эллипс с полуосями

(5.31)

с центром на оси Oz в точке и осями, параллельными соответственно осямОх и Оу. Из выражений (5.31) следует, что ,, т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (5.30) рассекается плоскостями, параллельными плоскостихОу.

Плоскость , параллельная плоскостиyOz, пересекает однополостный гиперболоид (5.30) по линии, выраженной уравнениями

, .

Если , то этими уравнениями определяется гипербола с центром в точке (, лежащая в плоскости, действительная ось которой параллельна осиОу, а мнимая – оси Oz. Полуоси этой гиперболы: (действительная полуось),(мнимая полуось).

Если , то уравнения линии сечения имеют вид

, .

Уравнения

,

являются уравнениями двух пересекающихся прямых:

, – первая прямая;

, – вторая прямая.

Аналогично уравнения ,являются уравнениями двух прямых:

, и ,.

Если , то в сечении получается гипербола, уравнения которой

, .

Действительная ось этой гиперболы параллельна оси Oz, а мнимая – оси Оу; центр лежит в точке .

Асимптоты всех гипербол, получающихся при пересечении однополостного гиперболоида (5.30) плоскостями , параллельны прямым, получающимся при пересечении гиперболоида плоскостями.

Сечения плоскостями , параллельными плоскостиxOz, аналогичны рассмотренным.

Все эти сечения дают представление о форме поверхности однополостного гиперболоида (5.30) (рис.3.14).