3.5. Эллиптический параболоид

Определение. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

, где. (5.34)

Будем считать, что . Если, то эллиптический параболоид (5.34) – это параболоид вращения, так как он получается вращением параболывокруг осиOz, являющейся осью параболы (рис.3.17).

Ось Oz является осью симметрии эллиптического параболоида (5.34) (она называется осью параболоида), а плоскости xOz и yOz – плоскостями симметрии (главные плоскости). Начало координат для эллиптического параболоида является точкой пересечения этой поверхности с ее осью и называется вершиной.

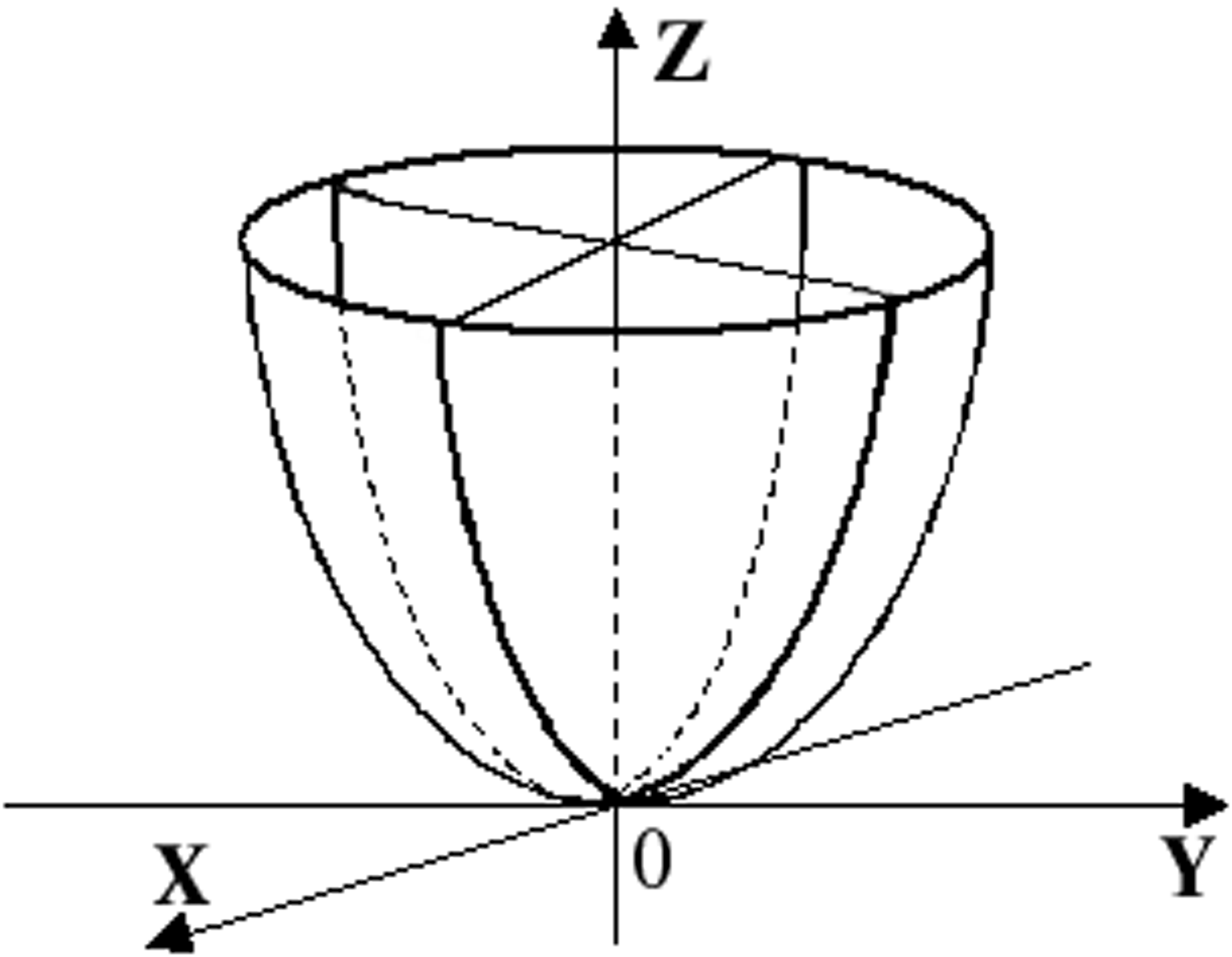
Рис. 3.17

Плоскость пересекает эллиптический параболоид (5.34) по линии

,. (5.35)

Если , то первое уравнение не имеет действительных рещшений, так как; это означает, что плоскостьприне пересекает эллиптический параболоид. Если, то, т.е. плоскостьхОу имеет с эллиптическим параболоидом только одну общую точку – вершину . Если, то, переписав уравнение (5.35) в виде,,

видим, что сечением является эллипс с центром в точке и полуосямии.

Плоскость xOz пересекает эллиптический параболоид (5.34) по параболе ,у = 0, а плоскость yOz – по параболе ,х = 0.

Таким образом, числа р и q – параметры парабол, получающихся в сечении параболоида его плоскостями симметрии (рис.3.17) .

Рассмотрим сечения эллиптического параболоида плоскостями, параллельными плоскости xOz, т.е. плоскостями, заданные уравнением .

Уравнения линии сечения: ,, или

,. (5.36)

Эти уравнения выражают параболу с вершиной в точке , ось симметрии которой одинаково направлена с осьюOz. Параметр параболы (5.36) равен р, т.е. параметру главного сечения элиптического параболоида плоскостью xOz (при этом t = 0).

Таким образом, эллиптический параболоид может быть образован параллельным переносом параболы (5.36), при котором вершина этой параболы перемещается по параболе ,х = 0, полученной пересечением эллиптического параболоида плоскостью yOz. Следовательно, плоскости этих парабол перпендикулярны, а оси параллельны и одинаково направлены.

Аналогичная картина получается и для сечений эллиптического параболоида (5.34) плоскостями, параллельными плоскости yOz.

3.6. Гиперболический параболоид

Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой спкциально выбранной прямоугольной системе координат имеет вид

, где. (5.37)

Для гиперболического параболоида (5.37) плоскости xOz и yOz являются плоскостями симметрии, а ось Oz – осью симметрии.

Ось симметрии гиперболического параболоида называется просто его осью. Точка, в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид (5.37) имеет вершину в начале координат.

Плоскости xOz и yOz, являющиеся для гиперболического параболоида (5.37) плоскостями симметрии, называются главными плоскостями гиперболического параболоида .

Гиперболический параболоид (5.37) в случае имеет только одну ось симметрии (осьОх), если же , то параболоид имеет еще две оси симметрии:и.

В самом деле, если координаты точки удовлетворяют уравнению, то этому же уравнению удовлетворяют координаты точки, симметричной с точкойотносительно прямой. Так же доказывается, что прямаяявляется осью симметрии.

Плоскость хОу пересекает гиперболический параболоид по двум прямым:

, или ,

и

.

Плоскость , параллельная плоскостихОу, пересекает гиперболический параболоид по гиперболе (рис.3.18, а)

. (5.38)

Если , то эти уравнения можно переписать в виде

.

Это гипербола, расположенная в плоскости с центром в точке, действительная ось которой параллельна осиОх, а мнимая – параллельна осиОу.

Если , то уравнения линии сечения можно представить в виде

.

Это гипербола, расположенная в плоскости с центром в точке, действительная ось которой параллельна осиОу, а мнимая – параллельна осиОх. Асимптоты всех гипербол, получающихся при пересечении гиперболического параболоида (5.37) плоскостями,, параллельны прямым, по которым этот параболоид пересекается с плоскостью.

Рис. 3.18

Плоскость xOz пересекает гиперболический параболоид по параболе (рис.3.18, б)

, (5.39)

а плоскость – по параболе

. (5.40)

Таким образом, числа p и q являются параметрами парабол, получающихся в сечении гиперболического параболоида (5.37) его главными плоскостями.

Рассмотрим сечения гиперболического параболоида (5.37) плоскостями, параллельными плоскости (рис.3.18, б), т.е. плоскостями, выраженными уравнением.

Уравнения линии сечения имеют вид

, или .

Эти уравнения выражают параболу с вершиной в точке , ось которой выражается уравнениями,у = 0, а направление оси совпадает с отрицательным направлением оси Oz. Параметр параболы

(5.41)

равен q, т.е. параметру главного сечения (5.40) гиперболического параболоида плоскостью yOz (t = 0).

Таким образом, гиперболический параболоид может быть образован параллельным переносом параболы (5.41), при котором вершина параболы (5.41) перемещается по параболе (5.39); плоскость параболы (5.39) перпендикулярна плоскости параболы (5.41), а оси этих парабол параллельны и противоположно направлены (рис.3.18, б).

Аналогичная картина получается и для сечений гиперболического параболоида плоскостями, параллельными плоскости xOz.

Гиперболический параболоид называют иногда седлообразной поверхностью.