§3. Параметрические уравнения прямой

Теорема. Параметрические уравнения прямой, проходящей через точкуМ₀(х₀,у₀) и имеющей направляющий вектор, в декартовой системе координат имеют вид

.

Доказательство.ПустьМ(х,у) – произвольная точка плоскости. ТочкаМ(х,у) будет лежать на данной прямой тогда и только тогда, когда векторыиколлинеарны, т.е. тогда и только тогда, когда они отличаются числовым множителем (т.е. пропорциональны)

(2.7)

или в координатах , откуда

.

Если tпринимает все действительные значения, то точкаМс этими координатами описывает всю данную прямую.

Вводя радиусы-векторы иточекМ₀иМ, можно соотношение (2.7) переписать так: , откуда

. (2.8)

Это параметрическое уравнение прямой в векторной форме, проходящей через точку и имеющей направляющий вектор.

§4. Уравнение прямой, проходящей через две точки

Теорема. Уравнение прямой, проходящей через две точкиМ₁(х₁,у₁) иМ₂(х₂,у₂), заданные относительно декартовой системы координат, можно записать в одном из следующих видов:

, (2.9)

или

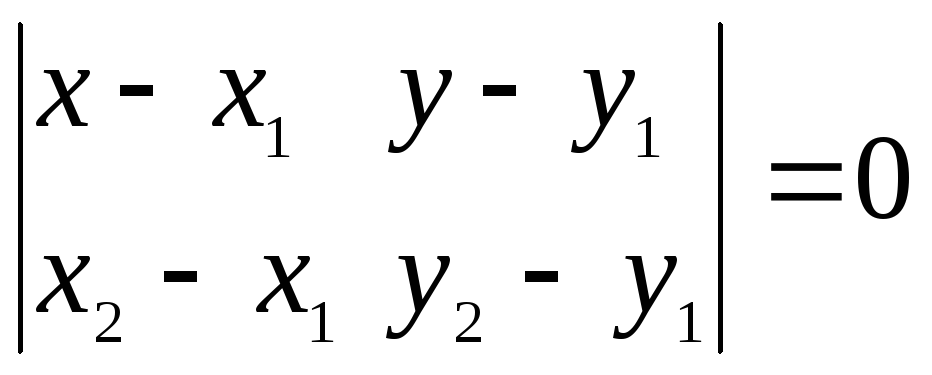, (2.10)

или

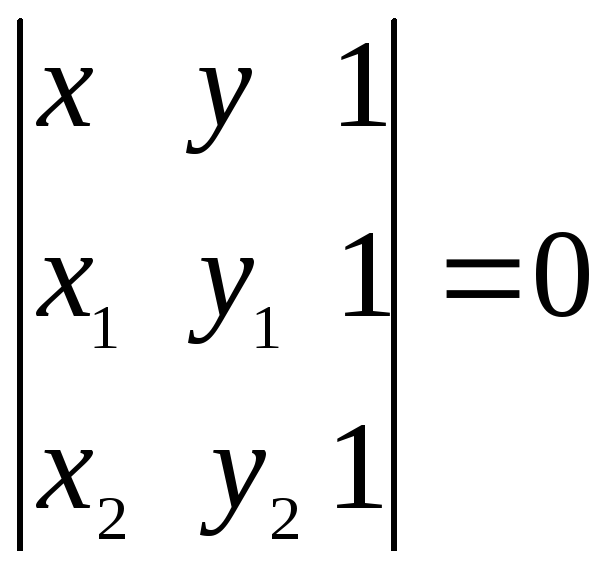, (2.11)

или в параметрической форме

.

Доказательство. За направляющий вектор прямой можно взять вектор

;

далее остается применить результаты §1 и §3.

§5. Уравнение прямой в отрезках

Пусть прямая не проходит через начало декартовой системы координат и пересекает обе оси координат: ось Ох в точке (а,0), а осьОу – в точке (0,b).

Абсцисса аи ординатаbточек пересечения прямой с осямиОх иОучасто называются отрезками, отсекаемыми прямой на осях координат.

Уравнение указанной прямой будет иметь вид

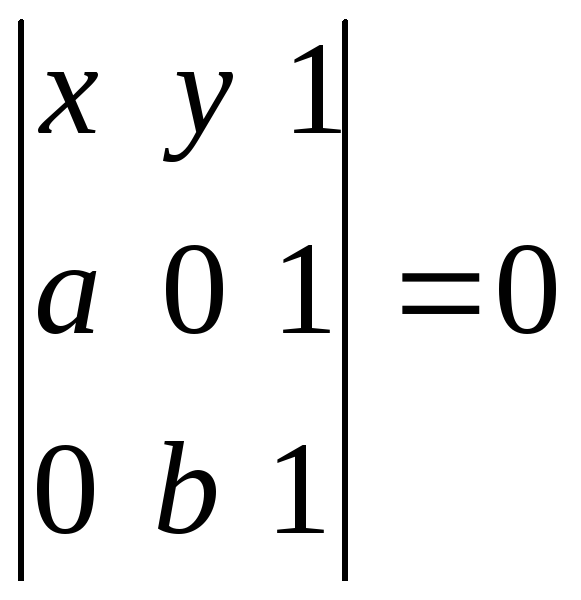или. (2.12)

Это уравнение называется уравнением прямой в отрезках.

§6. Угловой коэффициент прямой

Определение. Угловым коэффициентом kпрямой, заданной относительно декартовой прямоугольной системы координат, называется отношение второй координаты направляющего вектора этой прямой к его первой координате:

.

Прямые, параллельные оси Оу, и сама осьОуне имеют углового коэффициента, так какпервая координата любого направляющего вектора всех таких прямых равна нулю.

Для каждой прямой, пересекающей ось Оу, угловой коэффициент имеет вполне определенное значение, не зависящее от выбора направляющего вектора.

В самом деле, если и– два направляющих вектора одной и той же прямой, пересекающей осьОу, то они коллинеарны и, следовательно,

, (гдеи).

В декартовой прямоугольной системе координат угловой коэффициент kпрямой, пересекающей осьОу, равен тангенсу угла от осиОхдо направляющего вектора этой прямой: .

В самом деле, если угол от оси Ох до вектораравен, то на основании формул (4.2) книги 2 и при условии, что, координаты вектораравны

,

.

Из этих соотношений и следует, что

.

§7. Уравнение прямой с угловым коэффициентом

Уравнение прямой, проходящей через точку М₀(х₀,у₀) и имеющей угловой коэффициентk, в декартовой системе координат имеет вид

.(2.13)

Уравнение (2.13) следует из канонического уравнения прямой (§1). Это уравнение содержит множество всех прямых, принадлежащих пучку прямых с центром в точке М₀, кроме лишь прямой, перпендикулярной оси абсцисс (или параллельной осиОу).

Определение.Множество всех прямых, проходящих через одну точкуМ₀и лежащих в одной плоскости, называетсяпучком прямых с центром в точке М₀.

Уравнение прямой, имеющей угловой коэффициент kи пересекающей осьОув точке (0,b), в декартовой системе координат имеет вид

.(2.14)

Уравнение (2.14) следует из уравнения (2.13), если в нем положить .

Число bназывают иногданачальной ординатой этой прямой,а уравнение (2.14) –уравнением прямой с данной начальной ординатой и данным угловым коэффициентом.

Если прямая задана общим уравнением Ах + Ву + С = 0 в декартовой системе координат и, если эта прямая непараллельна осиОу, т.е., то, разделив это уравнение наВ, получим, откуда

или

, где.