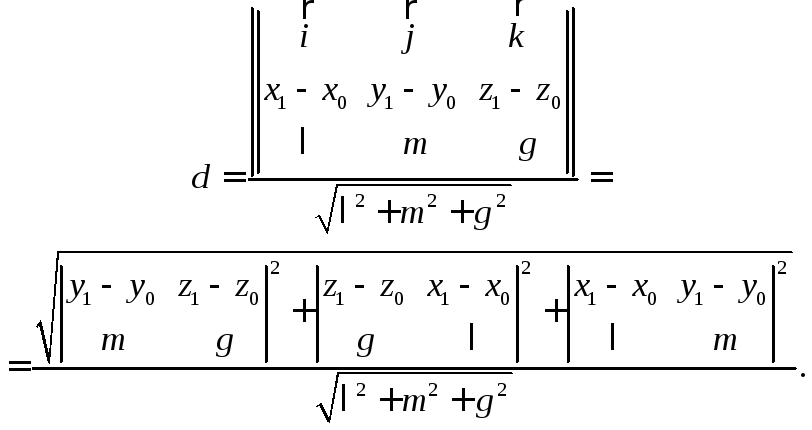- •Аналитическая геометрия
- •Глава 1 линии, поверхности и их уравнения
- •§1. Линия на координатной плоскости
- •§2. Поверхность в геометрическом пространстве
- •§3. Линия в геометрическом пространстве
- •§4. Алгебраические линии и поверхности
- •4.1. Алгебраические линии на плоскости
- •4.2. Алгебраические поверхности
- •§5. Полярная система координат на плоскости и в пространстве
- •5.1. Полярная система координат на плоскости
- •5.2. Полярная система координат в пространстве. Цилиндрические и сферические координаты
- •Глава 2 прямая линия на плоскости
- •§1. Уравнение прямой, проходящей через данную точку в данном направлении
- •§2. Общее уравнение прямой
- •§3. Параметрические уравнения прямой
- •§4. Уравнение прямой, проходящей через две точки
- •§5. Уравнение прямой в отрезках
- •§6. Угловой коэффициент прямой
- •§7. Уравнение прямой с угловым коэффициентом
- •§8. Взаимное расположение двух прямых
- •§9. Нормальное уравнение прямой
- •§10. Расстояние от точки до прямой
- •§11. Угол между двумя прямыми; условия коллинеарности и перпендикулярности двух прямых
- •Глава 3
- •§3. Условия перпендикулярности и компланарности вектора и плоскости, заданной общим уравнением
- •§4. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой
- •§5. Уравнение плоскости в отрезках
- •§6. Взаимное расположение двух плоскостей
- •6.1. Условие пересечения двух плоскостей и угол между ними
- •6.2. Условие параллельности двух плоскостей
- •6.3. Условие совпадения двух плоскостей
- •§7. Взаимное расположение трех плоскостей
- •§8. Нормальное уравнение плоскости
- •§9. Приведение общего уравнения плоскости к нормальному виду
- •§10. Расстояние от точки до плоскости
- •Глава 4 прямая и плоскость в трехмерном пространстве
- •§1. Уравнения прямой в трехмерном пространстве
- •1.1. Канонические и параметрические уравнения прямой
- •1.2. Уравнения прямой, проходящей через две точки
- •1.3. Прямая как линия пересечения двух плоскостей. Общее уравнение прямой
- •§2. Угол между двумя прямыми в трехмерном пространстве
- •§3. Условие принадлежности двух прямых одной плоскости
- •§4. Расстояние от точки до прямой в трехмерном пространстве
- •§5. Угол между прямой и плоскостью. Условие перпендикулярности прямой и плоскости
- •§6. Кратчайшее расстояние между двумя скрещивающимися прямыми
- •Глава 5 линии и поверхности второго порядка
- •§1. Линии второго порядка, заданные каноническими уравнениями
- •1.1. Эллипс
- •1.2. Гипербола
- •1.3. Парабола
- •§2. Приведение общего уравнения линии второго порядка к простейшему (каноническому) виду
- •§3. Поверхности второго порядка, заданные каноническими уравненниями
- •3.1. Эллипсоид
- •3.2. Однополостный гиперболоид
- •3.3. Двуполостный гиперболоид
- •3.4. Конус второго порядка
- •3.5. Эллиптический параболоид
- •3.6. Гиперболический параболоид
- •3.7. Цилиндры второго порядка
- •§4. Приведение общего уравнения поверхности второго порядка к каноническому виду
- •Упражнения
1.2. Уравнения прямой, проходящей через две точки
Уравнения
прямой, проходящие через две различные
точки
![]() и
и![]() ,
заданные относительно декартовой
системы координат, можно записать в
виде
,
заданные относительно декартовой
системы координат, можно записать в
виде
![]() ,
,
или, в параметрической форме
![]() .
.
Доказательство.За направляющий вектор прямой можно
взять вектор![]() ,
после чего остается применить результаты
предыдущего пункта.
,
после чего остается применить результаты
предыдущего пункта.
1.3. Прямая как линия пересечения двух плоскостей. Общее уравнение прямой
В общем случае прямую в декартовой системе координат можно задать уравнениями двух плоскостей
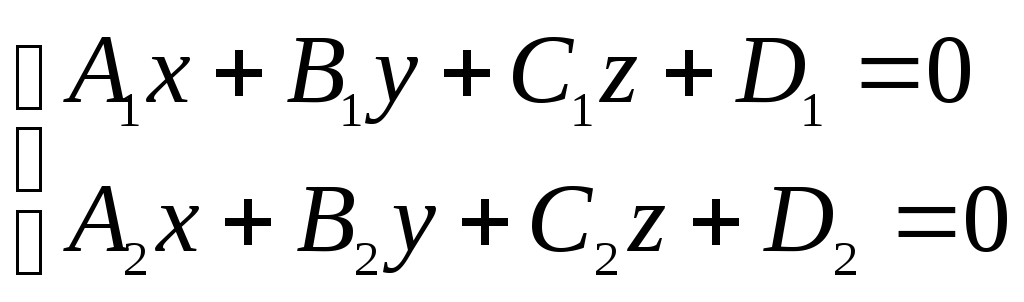 , (4.6)
, (4.6)
пересекающихся по этой прямой. Система (4.6) называется общим уравнением прямой в трехмерном пространстве.
Для
приведения прямой, заданной двумя
пересекающимися плоскостями (4.6), к
каноническому виду, надо найти какое-нибудь
решение
![]() системы (4.6). Точка
системы (4.6). Точка![]() лежит на прямой, по которой пересекаются
плоскости (4.6). Далее, вектор
лежит на прямой, по которой пересекаются
плоскости (4.6). Далее, вектор![]() с координатами
с координатами

является направляющим вектором данной прямой, так как он ненулевой и компланарен каждой из данных плоскостей. В самом деле, применяя необходимое и достаточное условие компланарности вектора и плоскости, получим
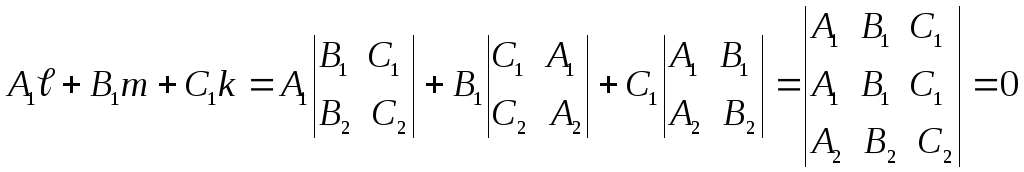
и, аналогично,
![]() ,
так что вектор
,
так что вектор![]() коллинеарен прямой, по которой пересекаются
плоскости (4.6).
коллинеарен прямой, по которой пересекаются
плоскости (4.6).
Тогда канонические уравнения прямой (4.6) можно записать в виде
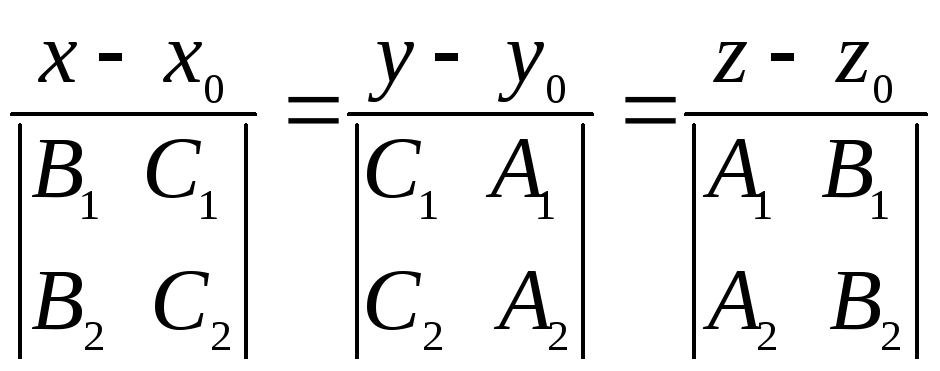 .
.
§2. Угол между двумя прямыми в трехмерном пространстве
Углом
между двумя прямыми в пространстве
называется любой из углов между двумя
параллельными им прямыми, проходящими
через некоторую точку пространства.
Таким образом, две прямые в пространстве
(если они не перпендикулярны) образуют
между собой два различных угла: один
острый, другой тупой. Сумма этих углов
равна
![]() .
.
Пусть
![]() и
и![]() – направляющие векторы данных прямых,
заданных относительно декартовой
прямоугольной системы координат. Угол
между этими векторами равен одному из
углов, образованных данными прямыми.
Следовательно, косинусы углов между
двумя данными прямыми выражается
формулой
– направляющие векторы данных прямых,
заданных относительно декартовой
прямоугольной системы координат. Угол
между этими векторами равен одному из
углов, образованных данными прямыми.
Следовательно, косинусы углов между
двумя данными прямыми выражается
формулой
![]() .
.
Отсюда получаем необходимое и достаточное условие перпендикулярности двух прямых:
![]() ;
;
для того, чтобы две прямые были взаимно перпендикулярны, необходимо и достаточно, чтобы сумма произведений соответствующих координат направляющих векторов этих прямых была равна нулю.
§3. Условие принадлежности двух прямых одной плоскости
Пусть две прямые заданы каноническими уравнениями
 (4.7)
(4.7)
Если
две прямые принадлежат одной и той же
плоскости, тогда их направляющие векторы
![]() ,
,![]() и вектор
и вектор![]() компланарны, т.е. смешанное произведение
компланарны, т.е. смешанное произведение
![]() .
.
Отсюда условие принадлежности прямых одной плоскости, записанное в координатной форме, имеет вид
 .
.
§4. Расстояние от точки до прямой в трехмерном пространстве
Пусть
в пространстве заданы точка
![]() и прямая каноническим уравнением
и прямая каноническим уравнением
![]()
относительно декартовой прямоугольной системы координат.
Расстояние
dот точкиМ1до прямой можно определить как высоту
параллелограмма, сторонами которого
служит вектор![]() и направляющий вектор
и направляющий вектор![]() прямой, отложенный от точкиМ0этой прямой. Поэтому для определения
расстоянияdрассмотрим
модуль векторного произведения:
прямой, отложенный от точкиМ0этой прямой. Поэтому для определения
расстоянияdрассмотрим
модуль векторного произведения:
![]() ,
,
но
![]() – высота параллелограмма, следовательно,
– высота параллелограмма, следовательно,
![]() ,
,
откуда
![]() .
.
Так
как
![]() ,
,![]() ,
то
,
то