§4. Алгебраические линии и поверхности

4.1. Алгебраические линии на плоскости

Определение 1. Линия на координатной плоскости называется алгебраической, если в некоторой декартовой прямоугольной системе координат уравнение линии является алгебраическим.

Алгебраическим уравнением называется уравнение, которое мы получим, приравняв нулю целую рациональную функцию, т.е. функцию, которая получается, если над аргументами и числами производятся только операции сложения и умножения. Например,

.

Замечание. Вычитание рассматривается как сложение, при котором одно из слагаемых умножено на –1, а деление на число, не равное нулю – как умножение на число, обратное этому числу.

Определение 2. Если линия определяется в декартовой прямоугольной системе координат алгебраическим уравнением п-й степени, то она называется алгебраической линией п-го порядка.

Степенью алгебраического уравнения

называется степень целой рациональной функции F, т.е. максимальное значение суммы показателей аргументов в выражении вида

,

суммой которых является функция F.

В приведенном выше примере функция z третьей степени.

Во всех декартовых системах координат алгебраическая линия определяется алгебраическим уравнением и имеет один и тот же порядок. Таким образом, алгебраический характер уравнения алгебраической линии и ее порядок инвариантны (т.е. неизменны) по отношению к преобразованию декартовой системы координат.

В аналитической геометрии на плоскости изучаются главным образом алгебраические линии первого и второго порядков, т.е. линии, заданные относительно декартовой системы координат уравнениями

, (1.4)

Данные уравнения называются общими уравнениями линий первого и второго порядка.

4.2. Алгебраические поверхности

Определение 1. Алгебраической поверхностью называется множество всех точек М(x,y,z) геометрического пространства, координаты которых в декартовой прямоугольной системе координат удовлетворяют алгебраическому уравнению

. (1.5)

Определение 2. Степень целой рациональной функции называетсяпорядком алгебраической поверхности.

Так же, как и для алгебраической линии, алгебраический характер уравнения (1.5) и порядок алгебраической поверхности инвариантны по отношению к преобразованию декартовой системы координат.

В аналитической геометрии в пространстве изучаются главным образом поверхности первого и второго порядка, т.е. поверхности, заданные относительно декартовой системы координат уравнениями

,

. (1.6)

Эти уравнения называются общими уравнениями поверхностипервого и второго порядка.

Таким образом, из вышесказанного следует, что линию и поверхность можно задать геометрически и аналитически с помощью уравнения. Для составления уравнений линий и поверхностей пользуются не только декартовой системой координат, но и другими, например, полярной системой координат.

§5. Полярная система координат на плоскости и в пространстве

5.1. Полярная система координат на плоскости

Говорят, что на плоскости введена полярная система координат, если на ней выбраны точка О, называемаяполюсом, полупрямаяОх, выходящая из точкиО, называемаяполярной осью, масштабный отрезокОЕ = 1 и указано положительное направление отсчета угла от осиОхдо любого луча, исходящего из полюсаО.

Положение любой точки М, не совпадающей с полюсом, на плоскости при помощи такой системы координат можно определить двумя числами: числом, выражающем расстояние точкиМ от полюса, и числом– величиной угла, образованного лучом, исходящим из полюса, содержащим отрезокОМс полярной осью. Положительным направлением отсчета угласчитается направление против часовой стрелки от осиОх. Упорядоченная пара чиселназывается полярными координатами точкиМ. Первая координатаназывается такжеполярным радиусом, а вторая ––полярным углом.

Тот факт, что числа иесть координаты точкиМ, записывают так:

. Для полюсаО считают= 0,– любое число.

Замечание. В некоторых случаях полярному радиусуприписывают знак: именно, считают, если уголизмеряют от полярной оси до луча, который образуется при продолжении отрезкаОМ за точкуО.

Полярные координаты иоднозначно определяют положение точки на плоскости. Обратное утверждение неверно, так как каждой точке координатной плоскости соответствует одно и то жеи бесчисленное множество полярных углов, которые могут отличаться друг от друга на, где. Таким образом, в отличие от декартовой системы координат, полярная система координат на плоскости не дает возможности установить взаимно однозначное соответствие между множеством всех точек координатной плоскости и множеством упорядоченных пар действительных чисел. Для того, чтобы получить взаимно однозначное соответствие, на полярный уголналагают ограничения:

(или).

Эти значения называются главными значениями полярного угла.

Установим связь между полярными и декартовыми координатами точки М. Для этого совместим правую прямоугольную систему координатхОус полярной так, чтобы начало координат совпало с полюсом, а полярная ось – с положительной полуосью абсцисс. Масштабный отрезокОЕполярной системы координат примем и за масштабный отрезок декартовой системы (рис.3.1).

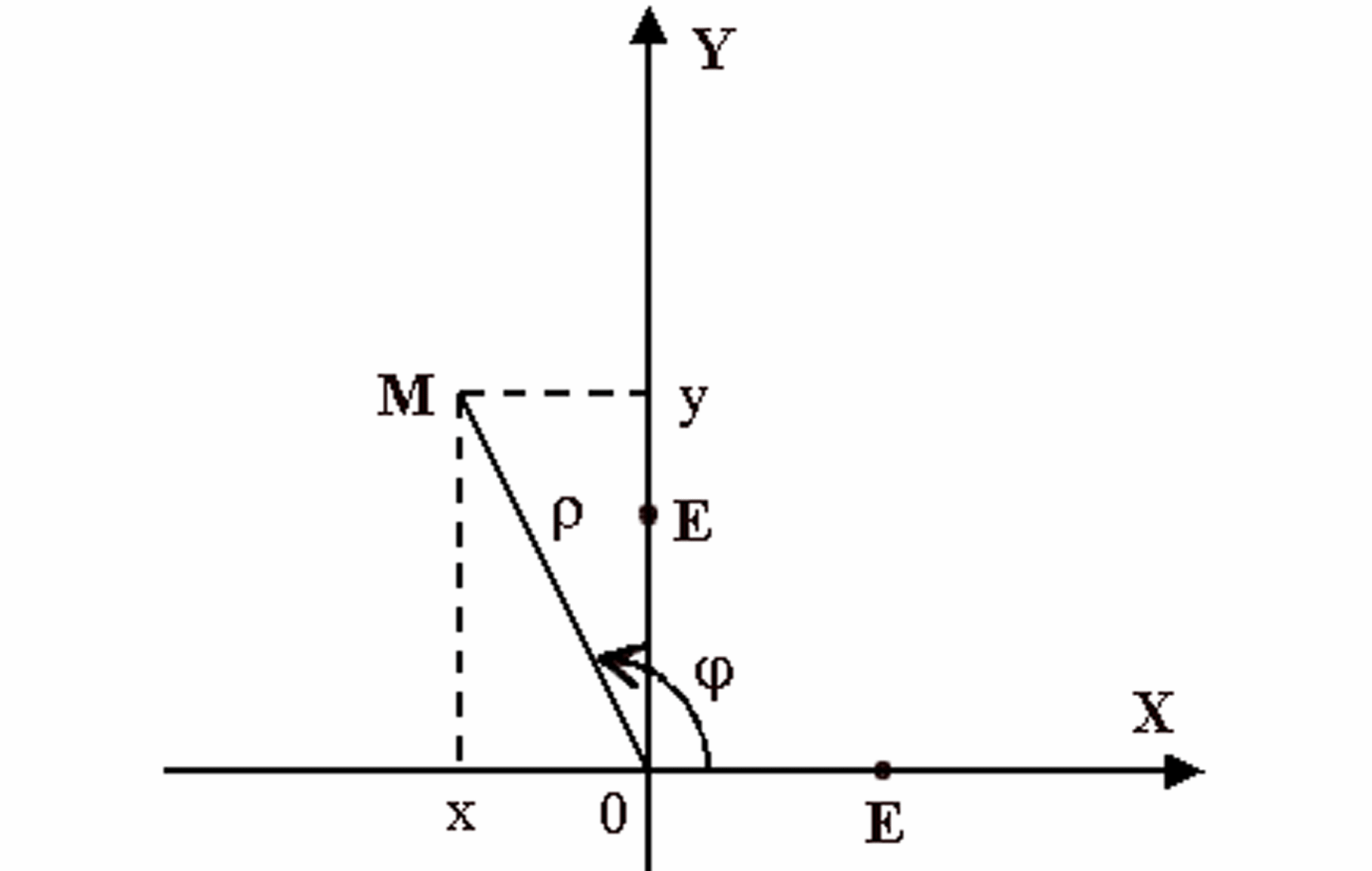
Рис. 3.1

Пусть и– полярные координаты произвольной точкиМ плоскости, не совпадающей с полюсом, ахиу– ее декартовы прямоугольные координаты в указанной выше системе.

По определению тригонометрических функций имеем

,(1.7)

Эти формулы выражают декартовы координаты точки плоскости через полярные. Решая систему (1.7) относительно и(при условии, что), получаем

, (1.8)

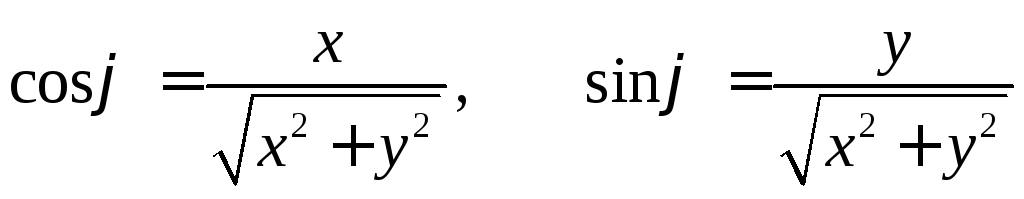(1.9)

или, если ,

. (1.10)

Формулы (1.8), (1.9), (1.10) позволяют вычислить полярные координаты иточкиМпо ее декартовым координатамхиу. При условии, что(т.е. рассматриваются главные значения полярного угла), из (1.9) получаем

В случае, если , то из (1.10) имеем

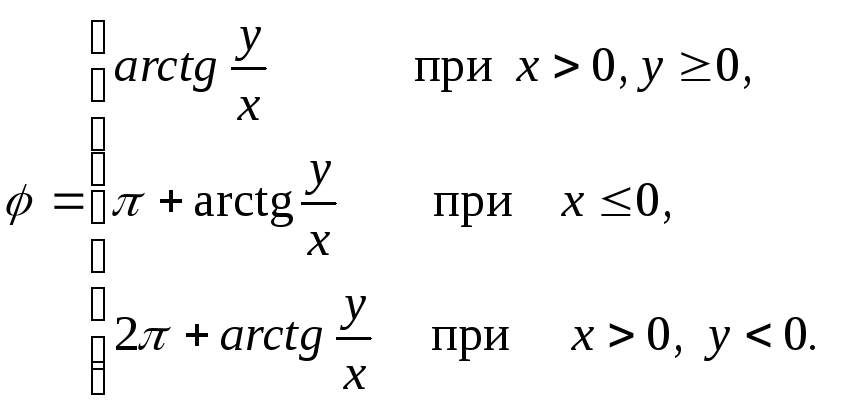
Уравнением линии в полярной системе координат называется уравнение

Φ(ρ, φ) = 0, (1.11)

которому удовлетворяют полярные координаты ивсех точек этой линии и только координаты таких точек.

В частности, уравнение линии в полярных координатах может иметь вид. Например, уравнение, гдеа = const, определяет в полярных координатах окружность с центром в полюсе и радиусомa; уравнение– окружность радиусаа, центр которой находится в точкеρ = а,φ= 0; уравнениеρ = аφ– кривую, которая называетсяспиралью Архимеда(изобразить такую кривую предлагается самостоятельно).