3.3. Двуполостный гиперболоид

Определение. Двуполостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

. (5.32)

Начало координат является центром симметрии (центр) двуполостного гиперболоида, оси координат – осями симметрии (главные оси), координатные плоскости – плоскостями симметрии (главные плоскости).

Если в уравнении (5.32) , то двуполостный гиперболоид (5.32) называетсядвуполостным гиперболоидом вращения, так как может быть получен вращением гиперболы

вокруг ее действительной оси Oz (рис.3.15).

Рис. 3.15

Вершинами двуполостного гиперболоида называются точки его пересечения с главной осью Oz.

Двуполостный гиперболоид (5.32) имеет две вершины .

Плоскости xOz и yOz пересекают двуполостный гиперболоид (5.32) по гиперболам

, и,.

Сечение двуполостного гиперболоида плоскостью выражается уравнениями

, .

Если , то первое уравнение не имеет действительных решений – плоскостьне пересекает поверхности.

Если , то

, откуда ,

плоскости встречают поверхность двуполостного гиперболоида в его вершинах. Если, то уравнения линии сечения можно переписать в виде

, .

Этими уравнениями выражается эллипс с полуосями

,

с центром в точке и осями, параллельными соответственно осямОх и Оу. Плоскость пересекает поверхность двуполостного гиперболоида по линии, выраженной уравнениями

, ,

или

, ,

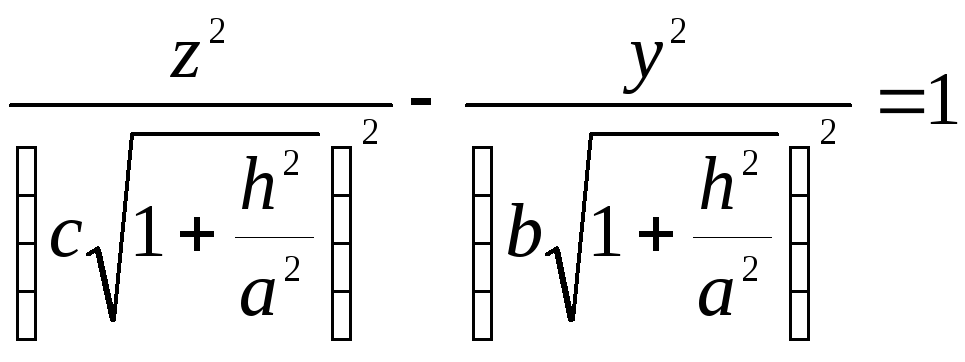т.е. по гиперболе с центром в точке , лежащей в плоскости. Действительная ось этой гиперболы параллельна осиOz, мнимая – оси Оу.

Аналогично исследуются сечения поверхности (5.32) плоскостями .

3.4. Конус второго порядка

Определение 1. Конусом второго порядка называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

(5.33)

(считаем, что в этом уравнии ). Начало координат, оси координат и координатные плоскости являются соответственно центром симметрии, осями симметрии и плоскостями симметрии и называютсявершиной, главными осями и главными плоскостями. Осью конуса (5.33) обычно называют ось Oz.

Основное свойство конуса: если на конусе (5.33)лежит точка (не совпадающая с вершиной), то на нем лежат все точки прямой, проходящей через вершинуО и эту точку М₀ (рис.3.16).

Рис. 3.16

В самом деле, если – произвольная точка, лежащая на прямой, то,y=λy₀, и поэтому

,

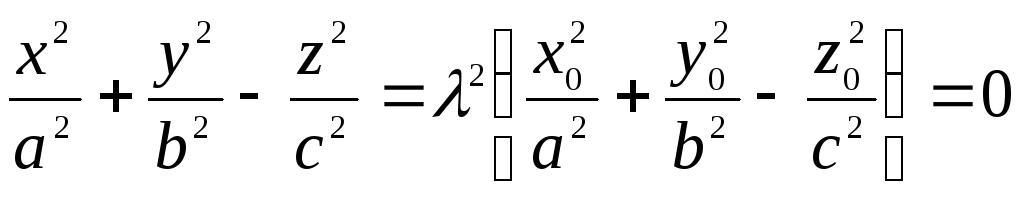а это значит, что точка принадлежит конусу.

Таким образом, поверхность (5.33) образована прямыми, проходящими через начало координат. Поэтому для представления вида этой поверхности достаточно рассмотреть ее сечение какой-нибудь плоскостью , параллельной плоскостихОу. В сечении получится эллипс, уравнения которого

, .

Центр этого эллипса лежит на оси Oz в точке , а значит, поверхность (5.33) образована прямыми, соединяющими начало координат со всеми точками эллипса (рис.3.16).

Исходя из основного свойства конуса второго порядка, дадим определение произвольной конической поверхности.

Определение 2. Конической поверхностью (или конусом) называется поверхность, образованная перемещением прямой, проходящей через одну и ту же точку и заданную кривую.

Перемещающаяся прямая называется образующей конуса, данная точка – вершиной, а заданная линия – направляющей.

По определению, уравнению конической поверхности должны удовлетворять координаты всех точек прямой образующей конуса, т.е. точки с координатами , где– любое действительное число;, а это значит, что функцияв уравнении, задающем коническую поверхность, должна быть однородной.

Определение 3. Функция называетсяоднородной, если она обладает следующими свойствами:

1. Если точка входит в область определения функции, то точка, где– любое действительное число, также входит в область определения этой функции;

2. Существует такое число k, что для любой точки из области определения функциии для любого числавыполняется соотношение

.

Число k называется показателем (степенью) однородности. Для конуса второго порядка (5.33) показатель однородности k = 2.