
- •Аналитическая геометрия
- •Глава 1 линии, поверхности и их уравнения
- •§1. Линия на координатной плоскости
- •§2. Поверхность в геометрическом пространстве
- •§3. Линия в геометрическом пространстве
- •§4. Алгебраические линии и поверхности
- •4.1. Алгебраические линии на плоскости
- •4.2. Алгебраические поверхности
- •§5. Полярная система координат на плоскости и в пространстве
- •5.1. Полярная система координат на плоскости
- •5.2. Полярная система координат в пространстве. Цилиндрические и сферические координаты
- •Глава 2 прямая линия на плоскости
- •§1. Уравнение прямой, проходящей через данную точку в данном направлении
- •§2. Общее уравнение прямой
- •§3. Параметрические уравнения прямой
- •§4. Уравнение прямой, проходящей через две точки
- •§5. Уравнение прямой в отрезках
- •§6. Угловой коэффициент прямой
- •§7. Уравнение прямой с угловым коэффициентом
- •§8. Взаимное расположение двух прямых
- •§9. Нормальное уравнение прямой
- •§10. Расстояние от точки до прямой
- •§11. Угол между двумя прямыми; условия коллинеарности и перпендикулярности двух прямых
- •Глава 3
- •§3. Условия перпендикулярности и компланарности вектора и плоскости, заданной общим уравнением
- •§4. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой
- •§5. Уравнение плоскости в отрезках
- •§6. Взаимное расположение двух плоскостей
- •6.1. Условие пересечения двух плоскостей и угол между ними
- •6.2. Условие параллельности двух плоскостей
- •6.3. Условие совпадения двух плоскостей
- •§7. Взаимное расположение трех плоскостей
- •§8. Нормальное уравнение плоскости
- •§9. Приведение общего уравнения плоскости к нормальному виду
- •§10. Расстояние от точки до плоскости
- •Глава 4 прямая и плоскость в трехмерном пространстве
- •§1. Уравнения прямой в трехмерном пространстве
- •1.1. Канонические и параметрические уравнения прямой
- •1.2. Уравнения прямой, проходящей через две точки
- •1.3. Прямая как линия пересечения двух плоскостей. Общее уравнение прямой
- •§2. Угол между двумя прямыми в трехмерном пространстве
- •§3. Условие принадлежности двух прямых одной плоскости
- •§4. Расстояние от точки до прямой в трехмерном пространстве
- •§5. Угол между прямой и плоскостью. Условие перпендикулярности прямой и плоскости
- •§6. Кратчайшее расстояние между двумя скрещивающимися прямыми
- •Глава 5 линии и поверхности второго порядка
- •§1. Линии второго порядка, заданные каноническими уравнениями
- •1.1. Эллипс
- •1.2. Гипербола
- •1.3. Парабола
- •§2. Приведение общего уравнения линии второго порядка к простейшему (каноническому) виду
- •§3. Поверхности второго порядка, заданные каноническими уравненниями
- •3.1. Эллипсоид
- •3.2. Однополостный гиперболоид
- •3.3. Двуполостный гиперболоид
- •3.4. Конус второго порядка
- •3.5. Эллиптический параболоид
- •3.6. Гиперболический параболоид
- •3.7. Цилиндры второго порядка
- •§4. Приведение общего уравнения поверхности второго порядка к каноническому виду
- •Упражнения
1.3. Парабола
Определение. Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемойфокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемойдиректрисой.
Расстояние от фокуса параболы до ее директрисы называется параметром параболы.
Эксцентриситет параболы – отношение расстояния любой точки параболы до фокуса к расстоянию ее до директрисы – есть постоянное число равное единице.
Найдем уравнение параболы. Возьмем такую систему координат хОу, чтобы ось абсцисс проходила через фокусF, перпендикулярно директрисех = Dпараболы, а ось ординат делила расстояние между фокусом и директрисой пополам (рис.3.11).
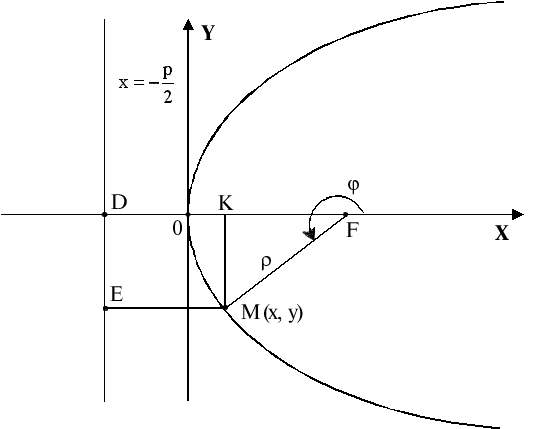
Рис. 3.11
Расстояние
FDмежду фокусом и
директрисой параболы обозначим черезр(параметр параболы). В выбранной
системе координат фокусFимеет координаты![]() ,
а уравнение директрисы есть
,
а уравнение директрисы есть![]() .
.
Пусть
![]() – произвольная точка плоскости. ТогдаМ, согласно определению, будет точкой
параболы тогда и только тогда, когда
– произвольная точка плоскости. ТогдаМ, согласно определению, будет точкой
параболы тогда и только тогда, когда![]() .
Так как
.
Так как
![]() ,
а
,
а![]() ,
,
то уравнение параболы
имеет вид
![]() .
.
Это уравнение
эквивалентно следующему: ![]() ,
,
или
![]() . (5.19)
. (5.19)
Уравнение (5.19) называется каноническим уравнением параболы.
Свойства параболы:
1. Сравнивая уравнения (5.19) и (5.2), убеждаемся в том, что парабола есть кривая второго порядка.
2.
Поскольку
![]() ,
то из уравнения (5.19) имеем
,
то из уравнения (5.19) имеем![]() .
Следовательно, парабола есть неограниченная
кривая, расположенная в правой
полуплоскости относительно осиОуи осьОхявляется осью симметрии
параболы (рис.3.11). Это единственная ось
симметрии параболы.
.
Следовательно, парабола есть неограниченная
кривая, расположенная в правой
полуплоскости относительно осиОуи осьОхявляется осью симметрии
параболы (рис.3.11). Это единственная ось
симметрии параболы.
Парабола не имеет центра симметрии, она не является центральной кривой.
Точка пересечения параболы с ее осью симметрии называется вершиной параболы.Парабола (5.19) имеет только одну вершину, которая лежит в начале координатО(0, 0).
3.
Уравнение
![]() ,
где
,
где![]() ,
определяет параболу с вершиной в начале
координат и осью симметрииОу.
Парабола расположена в верхней
полуплоскости относительно осиОх.
,
определяет параболу с вершиной в начале
координат и осью симметрииОу.
Парабола расположена в верхней
полуплоскости относительно осиОх.
Уравнение
![]() пишут часто в виде, разрешенном
относительно ординатыу:
пишут часто в виде, разрешенном
относительно ординатыу:
![]() ,
где
,
где![]() .
.
4.
Уравнение
![]() ,
где
,
где![]() ,
определяет параболу, которая симметрична
с параболой
,
определяет параболу, которая симметрична
с параболой![]() относительно осиОу, а уравнение
относительно осиОу, а уравнение![]() – параболу, которая симметрична с
параболой
– параболу, которая симметрична с
параболой![]() относительно осиОх.
относительно осиОх.
5. Найдем
полярное уравнение параболы. Пусть
полюс полярной системы координат
совпадает с фокусом параболы
![]() ,
а полярная ось – с положительным
направлением осиОх(рис.3.11). Полярные
координаты точки параболы
,
а полярная ось – с положительным
направлением осиОх(рис.3.11). Полярные
координаты точки параболы![]() обозначим через
обозначим через![]() и
и![]() ,
т.е.
,
т.е.![]() .
Из треугольникаFMKнаходим
.
Из треугольникаFMKнаходим![]() ,
,![]() .
.
Подставляя значения хиув уравнение (5.19), получаем
![]() ,
,
Откуда
![]() .
.
Учитывая,
что
![]() и
и![]() ,
имеем
,
имеем![]() .
.
Тогда полярное уравнение параболы есть
![]() . (5.20)
. (5.20)
§2. Приведение общего уравнения линии второго порядка к простейшему (каноническому) виду
Приведение общего уравнения
![]() (5.21)
(5.21)
линии второго порядка к простейшему виду означает преобразование его к такому виду, по которому легко определить, задает ли это уравнение кривую и какую именно (окружность, эллипс, гиперболу, параболу, прямую, точку).
Теорема 1. Общее уравнение (5.21) линии второго порядка, заданной относительно прямоугольной декартовой системы координатхОу, при помощи поворота и переноса осей координат можно привести к одному из следующих видов:
![]() где
где![]() ,
,
![]() ,
где
,
где![]() ,
,
![]() где
где![]() .
.
Эти уравнения будем называть простейшими уравнениями линии второго порядка.
Доказательство.
Докажем сначала, что можно повернуть
осихОу на такой угол![]() ,
что в преобразованном уравнении
коэффициент при произведении
,
что в преобразованном уравнении
коэффициент при произведении![]() новых
координат обратится в нуль. Итак,
предполагая, что
новых
координат обратится в нуль. Итак,
предполагая, что![]() (если
(если![]() ,
то эту часть доказательства можно
опустить), повернем осихОупока
на произвольный угол
,
то эту часть доказательства можно
опустить), повернем осихОупока
на произвольный угол![]() .
Тогда координатыхиуточкиМв системехОучерез координаты
.
Тогда координатыхиуточкиМв системехОучерез координаты![]() и
и![]() той же точкиМв системе
той же точкиМв системе![]() будут
выражаться соотношениями (см. кн.2, гл.8,
§1, п.1.1).
будут
выражаться соотношениями (см. кн.2, гл.8,
§1, п.1.1).
![]() или
или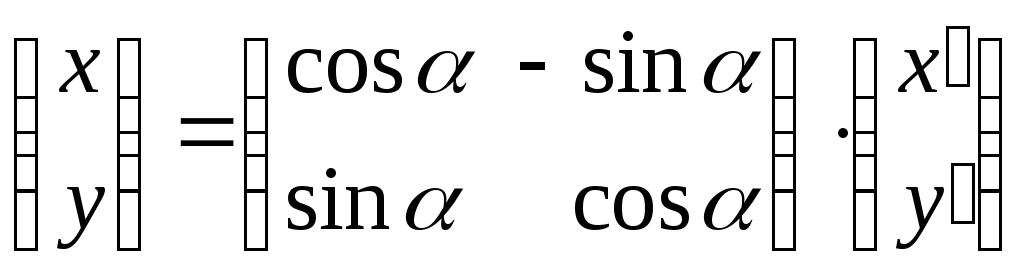 ,
,
где
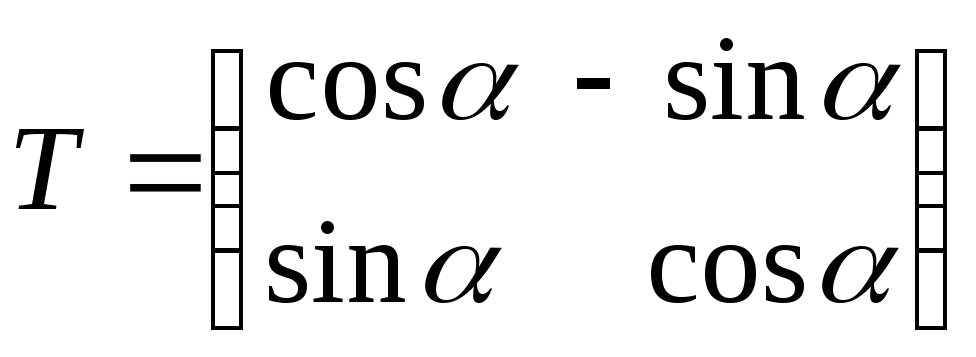 – матрица перехода,
– матрица перехода,![]() ,
а уравнение (5.21) примет вид
,
а уравнение (5.21) примет вид
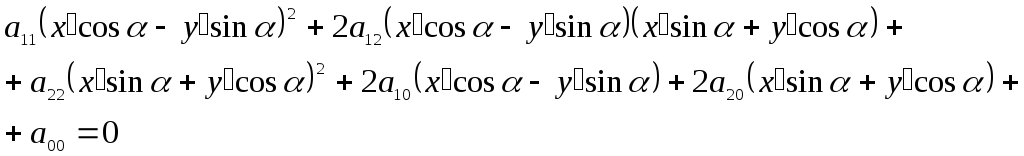
или
![]() ,
,
где

Условие
![]() принимает вид
принимает вид
![]() ,
,
откуда
![]() (5.22)
(5.22)
При
повороте на угол
![]() ,
определяемый этим соотношением, в
преобразованном уравнении коэффициент
,
определяемый этим соотношением, в
преобразованном уравнении коэффициент![]() обратится в нуль и оно примет вид
обратится в нуль и оно примет вид
![]() . (5.23)
. (5.23)
Отметим,
что при повороте системы координат на
угол
![]() ,
определяемый соотношением (5.22),
квадратичная форма
,
определяемый соотношением (5.22),
квадратичная форма
![]() ,
где
,
где![]() ,
,
содержащаяся в общем уравнении (5.21), приводится к каноническому виду (см. кн.2, гл.8, §3, п.3.1):
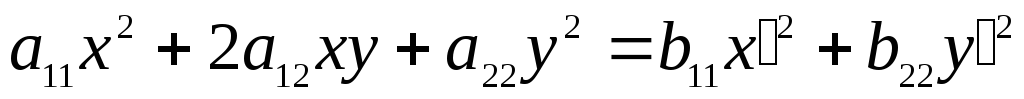 .
.
В этом
случае коэффициенты
![]() и
и![]() представляют собой собственные числа
представляют собой собственные числа![]() матрицы
матрицы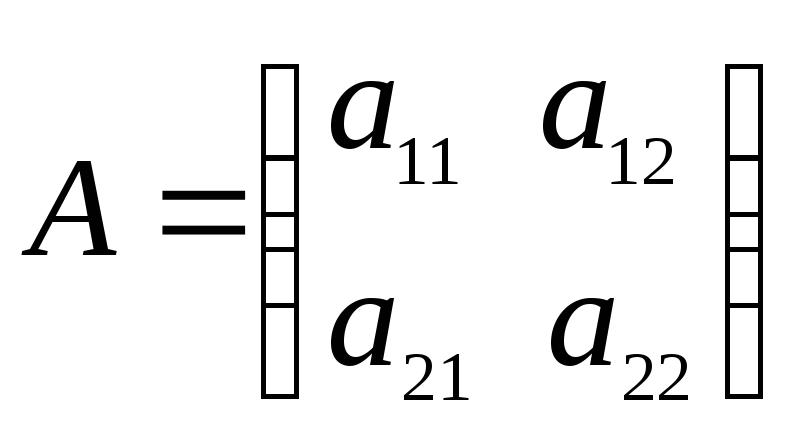 ,
где
,
где![]() ,
этой квадратичной формы. Следовательно,
они могут быть определены также и из
характеристического уравнения матрицыА:
,
этой квадратичной формы. Следовательно,
они могут быть определены также и из
характеристического уравнения матрицыА:
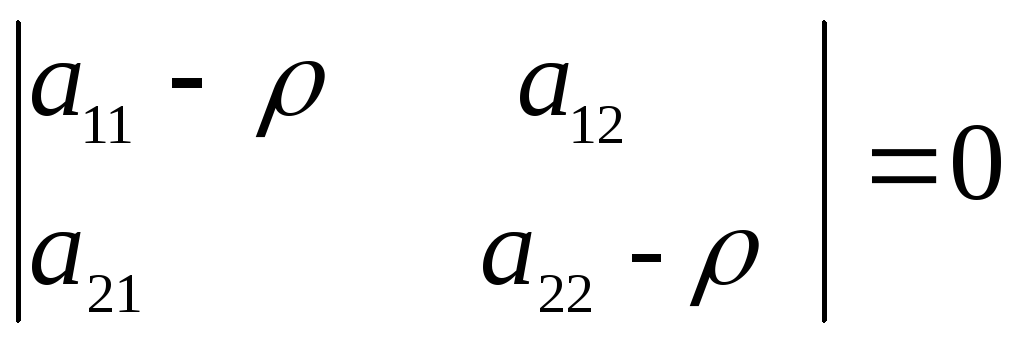 ,
,
или
![]() .
.
Отсюда находим
 ,
,
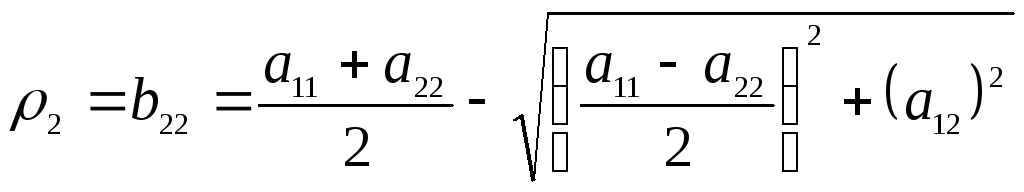 .
.
Чтобы привести уравнение (5.23) к простейшему виду, достаточно осуществить параллельный перенос системы координат.
1 случай:b11≠ 0,b22≠ 0.
Преобразуем уравнение (5.23) к виду

Производя
перенос осей
![]() так,
чтобы новым началом координат стала
точка
так,
чтобы новым началом координат стала
точка![]() (координаты этой точки даны относительно
системы
(координаты этой точки даны относительно
системы![]() ),
и, обозначая новую систему координат
через
),
и, обозначая новую систему координат
через![]() ,
будем иметь
,
будем иметь![]() так что уравнение (5.23) примет вид
так что уравнение (5.23) примет вид
![]() (5.24)
(5.24)
где
![]()
2 случай: илиb22= 0,b20≠ 0, илиb11= 0,b10≠ 0.
Предположим,
что b22= 0,b20≠ 0. Тогда уравнение (5.23) имеет вид![]()
или 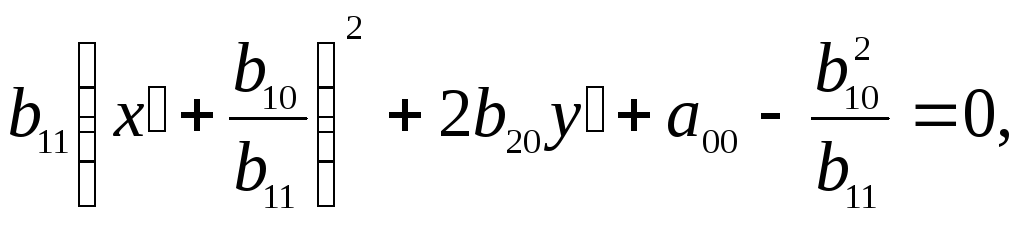
или 
Производя
перенос осей
![]() так,
чтобы новым началом координат стала
точка
так,
чтобы новым началом координат стала
точка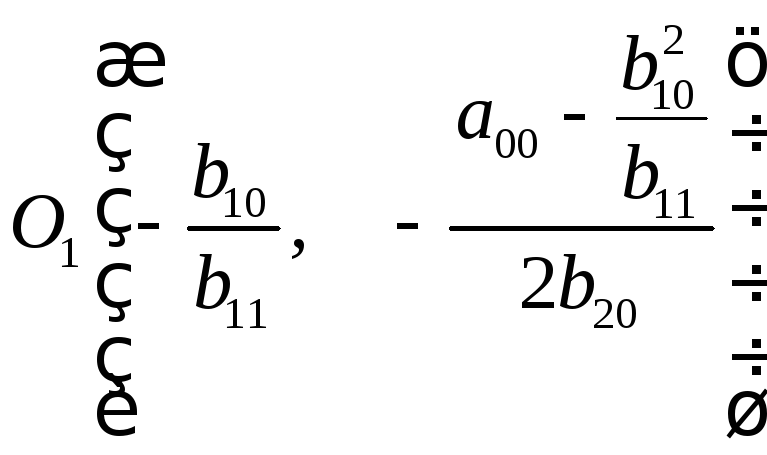 (координаты этой точки даны относительно
системы
(координаты этой точки даны относительно
системы![]() ),
и обозначая новую систему через
),
и обозначая новую систему через![]() будем
иметь
будем
иметь![]()
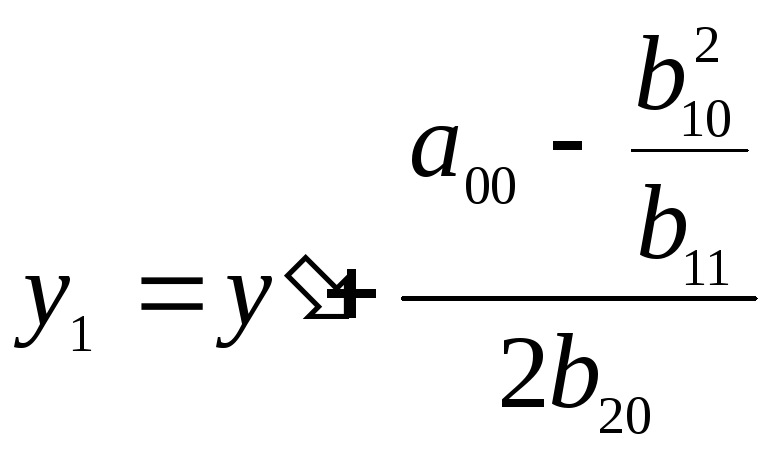 ,
так что, уравнение (5.23) примет вид
,
так что, уравнение (5.23) примет вид
![]() (Это уравнение параболы).
(Это уравнение параболы).
3
случай: или![]() или
или![]()
Предположим,
что
![]() Тогда уравнение (5.23) имеет вид
Тогда уравнение (5.23) имеет вид
![]() или
или
Перенося
оси
![]() так,
чтобы новым началом координат стала
точка
так,
чтобы новым началом координат стала
точка![]() и обозначая новую систему координат
через
и обозначая новую систему координат
через![]() будем иметь
будем иметь![]() так,
что уравнение (5.23) примет вид
так,
что уравнение (5.23) примет вид
![]() где
где![]()
Теорема 2.Общее уравнение (5.21) линии второго порядка, заданное относительно прямоугольной декартовой системы координат, определяет одну из следующих девяти линий (см. таблицу).
Доказательство. В предыдущей теореме было доказано, что если общее уравнение (5.21) линии второго порядка задано относительно декартовой прямоугольной системы координат, то оно при помощи преобразования прямоугольной системы координат в прямоугольную может быть приведено к одному из следующих простейших видов:
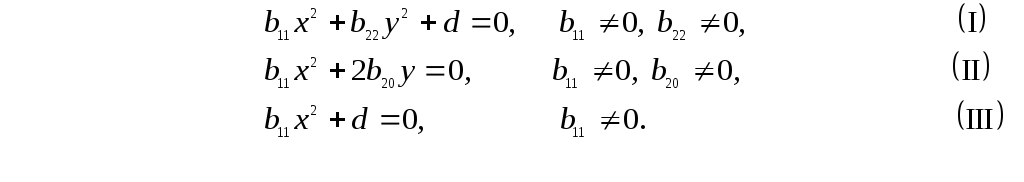 Здесь
через х
и у
мы обозначаем координаты точек в той
системе координат, в которой уравнение
линии является простейшим.
Здесь
через х
и у
мы обозначаем координаты точек в той
системе координат, в которой уравнение
линии является простейшим.
Таблица
|
Группа |
№п.п. |
Уравнение линии |
Название линии |
|
I |
1 |
|
Эллипс |
|
2 |
|
Мнимый эллипс | |
|
3 |
|
Две мнимые пересекающиеся прямые | |
|
4 |
|
Гипербола | |
|
5 |
|
Две пересекающиеся прямые | |
|
II |
6 |
|
Парабола |
|
III |
7 |
|
Две параллельные прямые |
|
8 |
|
Две мнимые параллельные прямые | |
|
9 |
|
Две совпадающие прямые |
Рассмотрим,
какой вид могут принять простейшие
уравнения
![]() линии второго порядка в зависимости от
знаков коэффициентов этих уравнений.
линии второго порядка в зависимости от
знаков коэффициентов этих уравнений.
(І):
1. Если
![]() и
и![]() одного знака, аd
имеет противоположный знак, то, деля
обе части уравнения (I)
на – d
и полагая
одного знака, аd
имеет противоположный знак, то, деля
обе части уравнения (I)
на – d
и полагая
![]() ,
приведем уравнение (I)
к виду
,
приведем уравнение (I)
к виду
![]() ,
,
– это каноническое уравнение эллипса.
2.
Если
![]() и
и![]() иd
одного знака, то уравнение (I)
приводится к виду
иd
одного знака, то уравнение (I)
приводится к виду
![]()
и
определяет мнимый эллипс (на мнимом
эллипсе нет, очевидно, ни одной точки
(действительной), так как х
и у
– действительные числа, то ![]() .
.
3.
Если
![]() и
и![]() одного знака, аd
= 0, то уравнение (I)
приводится к виду
одного знака, аd
= 0, то уравнение (I)
приводится к виду
![]() .
.
Это уравнение удовлетворяется только при х = у = 0. Но так как
![]() ,
,
то говорят, что это
уравнение распадается на пару мнимых
прямых
![]() ,
пересекающихся в действительной точкеО1(0, 0).
,
пересекающихся в действительной точкеО1(0, 0).
4. Если
![]() и
и![]() разных знаков, а
разных знаков, а![]() ,
то уравнение (I) приводится
к виду
,
то уравнение (I) приводится
к виду
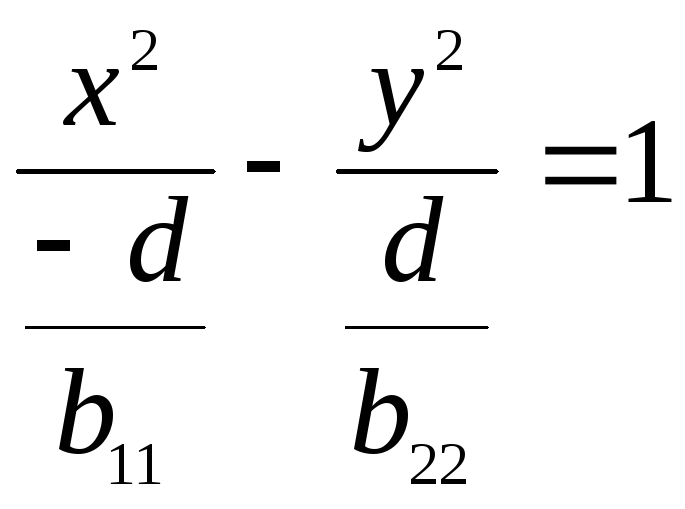 .
.
Считая,
что
![]() и полагая
и полагая![]() ,
получим каноническое уравнение гиперболы
,
получим каноническое уравнение гиперболы
![]()
(если
![]() ,
то получим
,
то получим![]() и, производя поворот осей на угол 90º,
т.е. полагая
и, производя поворот осей на угол 90º,
т.е. полагая![]() ,
,![]() ,
будем иметь
,
будем иметь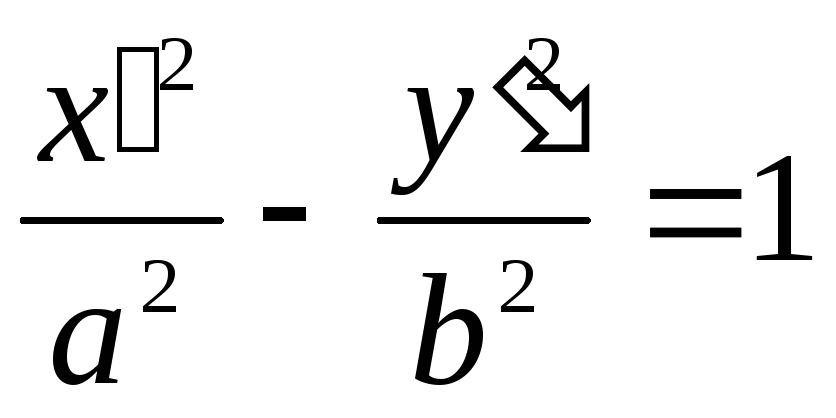 ).
).
5. Если
![]() и
и![]() разных знаков, а
разных знаков, а![]() ,
то уравнение (I) приводится
к виду
,
то уравнение (I) приводится
к виду![]() и определяет две пересекающиеся прямые:
и определяет две пересекающиеся прямые:
![]() .
.
(II).
Уравнение (II) можно привести
к виду![]() ,
где
,
где![]() Числорможно считать положительным,
так как в противном случае достаточно
изменить положительное направление
осиОуна противоположное.
Числорможно считать положительным,
так как в противном случае достаточно
изменить положительное направление
осиОуна противоположное.
(III). Уравнение (III) приводится к виду
![]() ,
или
,
или![]()
в зависимости от того, будет
![]() или же
или же![]() .
.
Уравнение
![]() определяет две параллельные прямые
определяет две параллельные прямые![]() и
и![]() .
.
Уравнению
![]() на множестве действительных чисел
отвечает пустое множество точек и оно
определяет две мнимые параллельные
прямые
на множестве действительных чисел
отвечает пустое множество точек и оно
определяет две мнимые параллельные
прямые![]() и
и![]() .
.
Уравнение
![]() определяет две совпадающие прямые –
ось абсцисс.
определяет две совпадающие прямые –
ось абсцисс.
Пример.Привести уравнение кривой
![]()
к каноническому виду и построить кривую, определяемую данным уравнением.
Определим
на какой угол αнеобходимо повернуть
систему координат, чтобы в преобразованном
уравнении коэффициент![]() Для этого воспользуемся условием (5.12)
Для этого воспользуемся условием (5.12)
![]()
откуда
![]()
Предоставляем
читателю убедиться в том, что какой бы
угол αмы ни выбрали, или![]() ,
или
,
или![]() ,
в конечном итоге мы придем к одной и той
же кривой. Для нашего рассмотрения
выберем
,
в конечном итоге мы придем к одной и той
же кривой. Для нашего рассмотрения
выберем![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]()
![]()
и уравнение кривой в
системе координат
![]() принимает
вид
принимает
вид

Выделим в левой части этого уравнения полный квадрат:
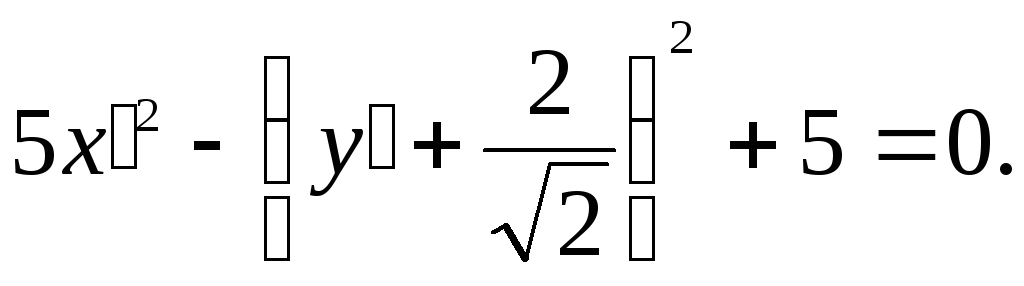
Осуществим
параллельный перенос системы координат
![]() по
формулам:
по
формулам:
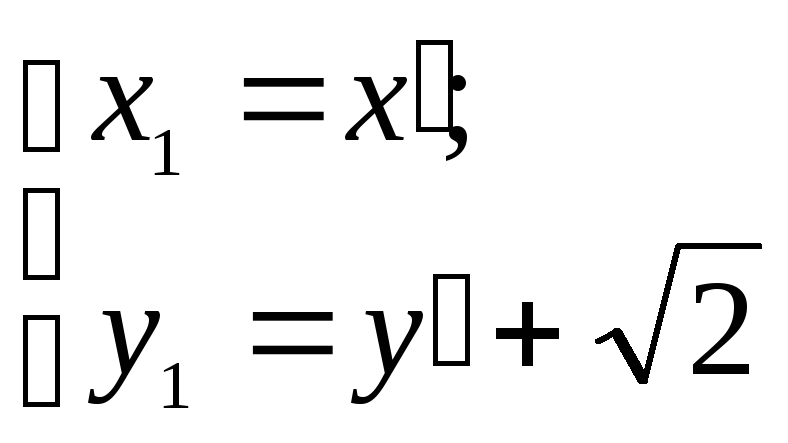 или
или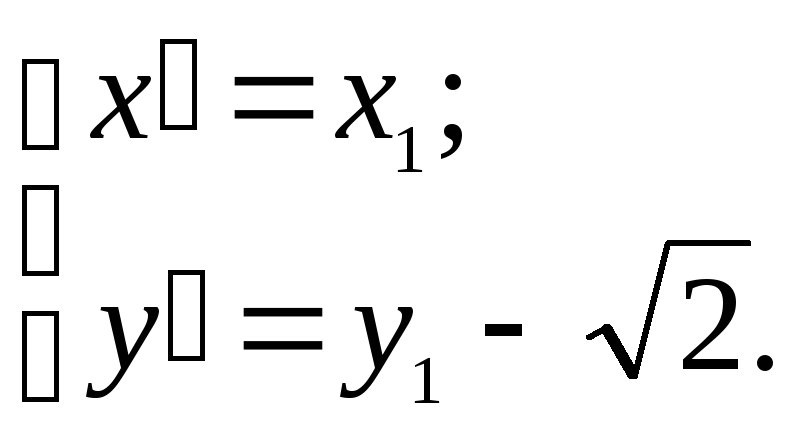
Тогда
получим в системе координат
![]()
![]()
откуда
![]()
Теперь
производя поворот осей
![]() на угол
на угол![]() (или
(или![]() ),
т.е. полагая
),
т.е. полагая![]() ,
,![]() ,
будем иметь
,
будем иметь![]() Это уравнение определяет гиперболу с
полуосями
Это уравнение определяет гиперболу с
полуосями![]() и
и![]() (рис.3.12).
(рис.3.12).
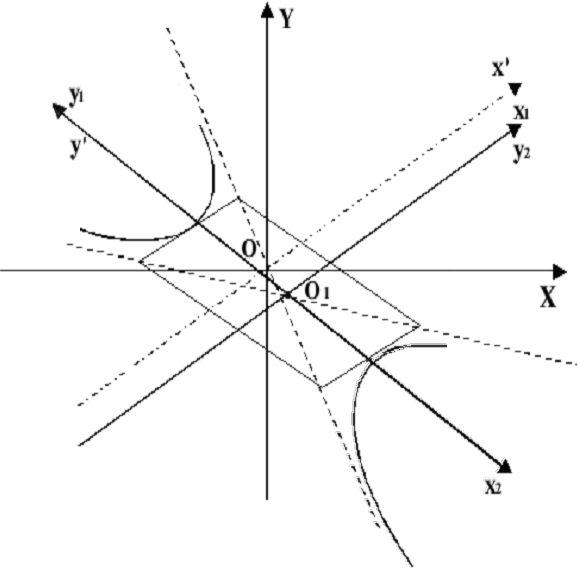
Рис. 3.12
