6.3. Условие совпадения двух плоскостей

Если плоскости (3.12) и (3.13) совпадают, то ранги основной и расширенной матриц системы, состоящей из уравнений (3.12) и (3.13), должны совпадать (система совместна) и быть равными единице (нормальные вектора иколлинеарны), т.е.

=.

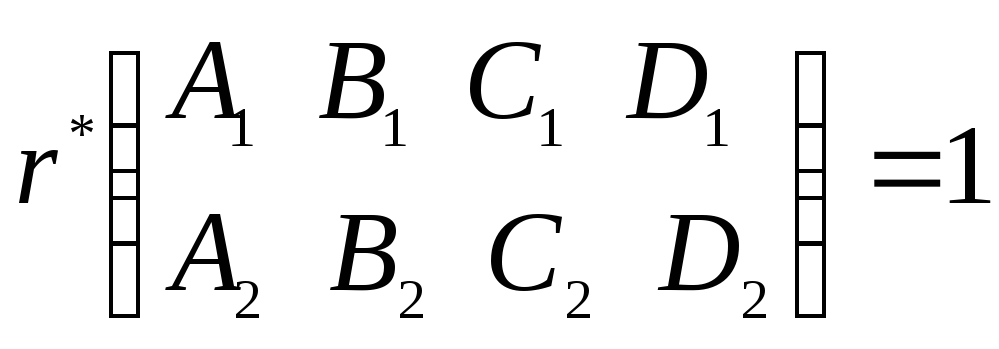Отсюда получаем условие совпадения плоскостей

,

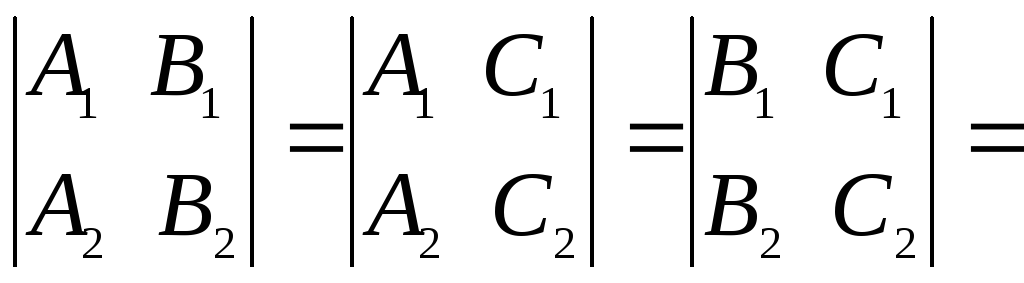
или

.

§7. Взаимное расположение трех плоскостей

Пусть относительно декартовой прямоугольной системы координат x, y, zзаданы три плоскости общими уравнениями

(3.17)

На основании предыдущего получаем следующие необходимые и достаточные условия взаимного расположения трех плоскостей.

1. Если определитель основной матрицыне равен нулю, то три данные плоскости имеют и притом только одну общую точку, так как в случаесистема (3.17) имеет и притом только одно решение: это решение, т.е. координаты единственной общей точки, принадлежащей трем данным плоскостям, мы получим, решив систему (3.17) (например, по формулам Крамера).

2. Если , а ранграсширенной матрицы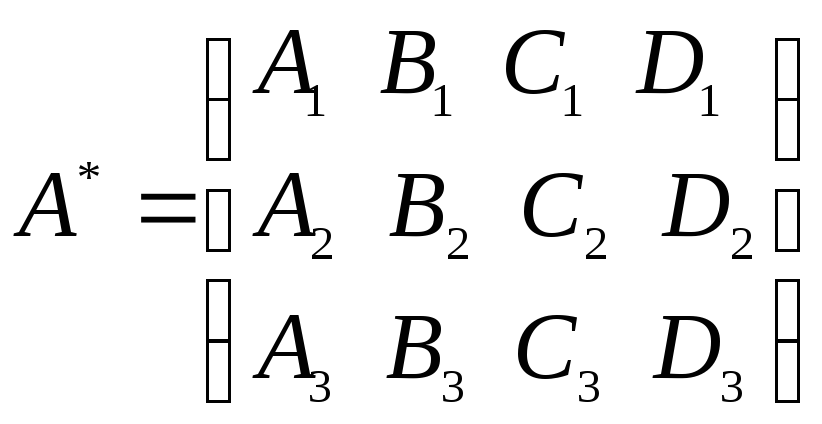равен трем и среди нормальных векторов,инет коллинеарных, то система несовместна (>); плоскости попарно пересекаются, причем прямые пересечения попарно различны.

3. Если ,, и среди нормальных векторов,иесть два коллинеарных (все три не могут быть коллинеарны, так как), то система несовместна; причем две плоскости параллельны, а третья их пересекает.

4. Если ,и среди нормальных векторов,инет коллинеарных, то плоскости попарно различны и проходят через одну прямую.

5. Если ,и среди нормальных векторов,иесть два коллинеарных, то две плоскости совпадают, а третья их пересекает.

6. Если , но коэффициенты любой пары уравнений (3.17) непропорциональны, то плоскости попарно параллельны.

7. Если , но среди уравнений (3.17) есть только два уравнения, коэффициенты которых пропорциональны, то две плоскости совпадают, а третья им параллельна.

8. Если , т.е. коэффициенты всех уравнений пропорциональны, то все плоскости совпадают.

§8. Нормальное уравнение плоскости

Пусть дана некоторая плоскость, не проходящая через начало координат. Проведем из начала координат (точки О) луч, перпендикулярный к плоскости. Точку пересечения луча с плоскостью обозначим буквойР, а длину перпендикуляраОР– черезр (рис.3.6).

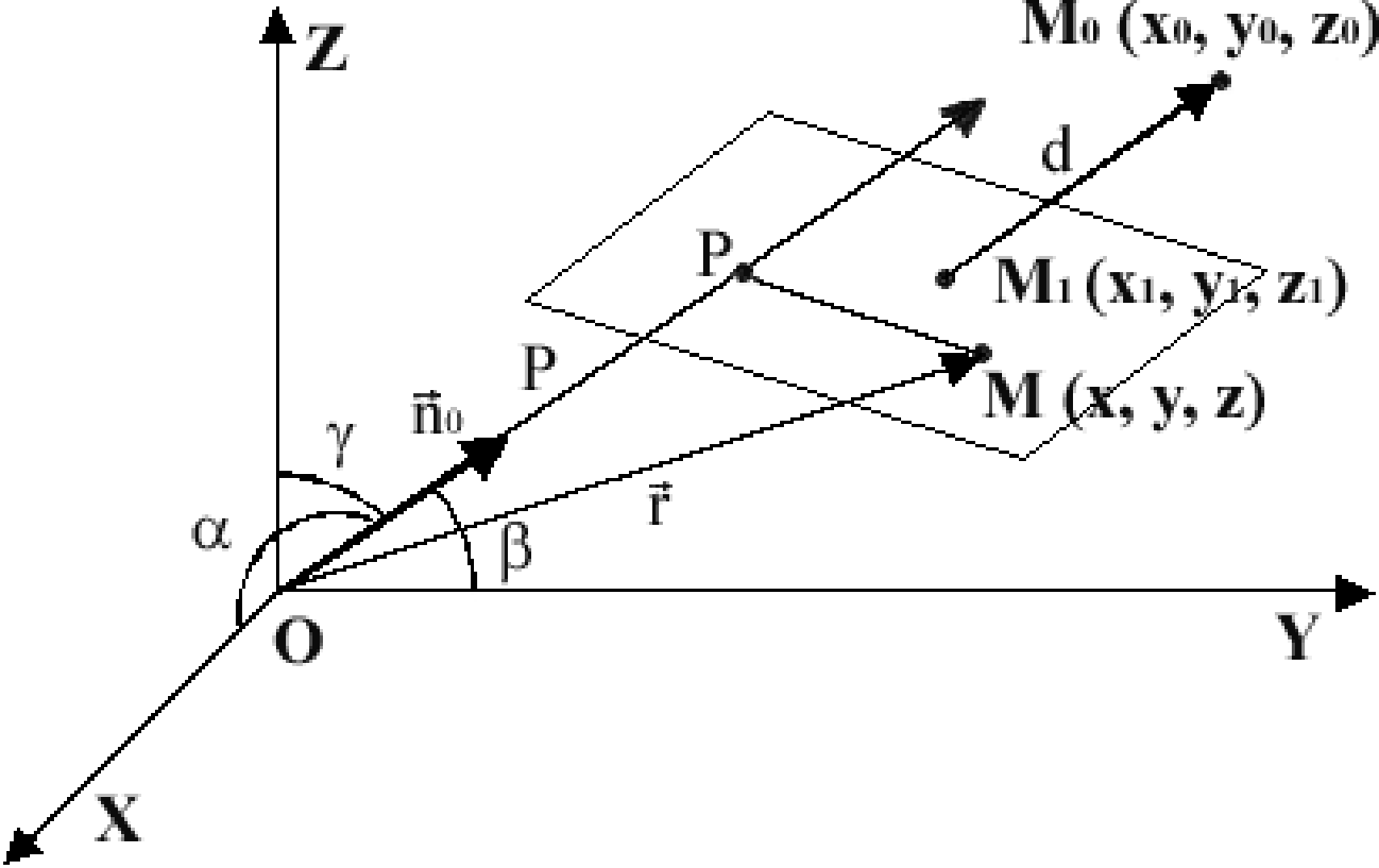
Рис. 3.6

Выберем на луче единичный векторс направляющими косинусами углов. Положительным направлениембудем считать направление отОкР. Составим уравнение плоскости, считая известными длинуи углы наклонавекторак осямOx, Oy, Oz соответственно.

Возьмем произвольную точку . Эта точка принадлежит заданной плоскости тогда и только тогда, когда проекция ее радиуса-векторана лучравнар; эту проекцию можно найти как скалярное произведениена единичный вектор:

.

Отсюда получаем уравнение

, (3.18)

которое называется нормальным уравнением плоскости.

Заметим, что для косинусов направляющих углов луча выполняется равенство

. (3.19)

Таким образом, уравнение плоскости, заданной относительно декартовой прямоугольной системы координат, называетсянормальным, если сумма квадратов коэффициентов при переменных равна 1, а свободный член есть отрицательное число; т.е. если

(3.20)

В векторной форме нормальное уравнение плоскости имеет вид

или.

Если плоскость проходит через начало координат, то р = 0, а направление вектора можно выбирать произвольно.