
- •Введение
- •3 Разработка общей структуры системы управления промышленным роботом
- •3.1 Особенности управления роботом как механической системой
- •3.2 Типовые структуры систем управления промышленными роботами
- •3.4 Датчики обратных связей промышленного робота
- •4.1 Решение задач кинематики
- •4.2 Решение прямой задачи динамики
- •5.1 Общая характеристика методов синтеза сау по их эталонным мм
- •7 Визуализация и архивирование технологического процесса
- •7.1 Выбор scada системы
- •7.2 Scada система trace mode
- •7.2.1 Общая структура и возможности trace mode
- •7.2.2 Исполнительные модули trace mode
- •7.2.3 Trace mode 6 - синтез новых технологий
- •7.3 Графическое отображение состояния производственных процессов
- •7.3.1 Назначение программы
- •7.3.2 Требования к аппаратным и программным ресурсам
- •7.3.3 Схема работы и возможности программы графического отображения состояния производственных процессов
- •7.3.4 Запуск и работа программы графического отображения
- •7.3.5 Система архивов trace mode
- •7.4 Сервер производственного контроля
- •7.4.1 Назначение сервера
- •7.4.2 Анализ информационных потребностей фирмы
- •7.4.3 Выбор сетевой ос
- •7.4.4 Выбор сетевых протоколов
- •7.4.5 Протокол 1-Wire
- •7.4.6 Стек протоколов tcp/ip
- •7.4.7 Протокол ррр
- •7.5 Web-сервер
- •7.6 Информационная безопасность
- •7.7 Резервное копирование
- •9.Безопасность и экологичность проекта
- •9.1 Биологическое действие лазерного излучения
- •9.2 Расчет общего освещения методом коэффициента использования светового потока
- •Расчет местного освещения
- •Расчет защитного заземления
- •9.5 Экологичность проекта
- •Список использованных источников
4.2 Решение прямой задачи динамики
При исследовании динамики манипуляторов составляют расчетную динамическую модель, учитывающую не только геометрические размеры звеньев и распределение кинематических пар, как при составлении кинематической модели, но и распределение масс звеньев и других элементов манипулятора, участвующих в движении. Могут быть учтены и другие свойства манипулятора, например упругие свойства его элементов. В этом случае числостепеней свободы системы становится больше числа степеней подвижности манипулятора, которое определяют как число независимых управляемых движений манипулятора (для манипуляторов с разомкнутой кинематической цепью оно равно числу приводов).
В аналитической механике имеются различные принципы и методы для составления дифференциальных уравнений движения механических систем любой сложности. Далее будем использовать уравнения Лагранжа второго рода [19].
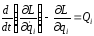 , (4.2)
, (4.2)
где
L – функция Лагранжа
(L=K-P);KиP –
полные кинетическая и потенциальная
энергия системы;qi
– обобщенные
координаты;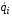 –
первая производная по времени обобщенных
координат;Qi
– обобщенные
силы (силы или моменты, развиваемые
приводами, а также внешние силы или
моменты, например
возникающие при взаимодействии
инструмента и обрабатываемой
поверхности), создаваемые в i-м
сочленении для реализации заданного
движения i-го
звена.
–
первая производная по времени обобщенных
координат;Qi
– обобщенные
силы (силы или моменты, развиваемые
приводами, а также внешние силы или
моменты, например
возникающие при взаимодействии
инструмента и обрабатываемой
поверхности), создаваемые в i-м
сочленении для реализации заданного
движения i-го
звена.
Запишем уравнение (5.1) в векторно-матричной форме:
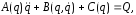 (4.3)
(4.3)
где
A(q) –
матрица инерционных коэффициентов,
зависящих от обобщенных координат;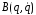 – вектор сил и моментов сил инерции,
зависящих от обобщенных координат и
скоростей; С(q) – вектор
сил и моментов сил тяжести;Q –
вектор обобщенных сил.
– вектор сил и моментов сил инерции,
зависящих от обобщенных координат и
скоростей; С(q) – вектор
сил и моментов сил тяжести;Q –
вектор обобщенных сил.
Рассмотрим
степени подвижности манипулятора со
структурной схемой, приведенной на
рисунке 5.1 по координатам
 .
Звенья манипулятора имеют массы
.
Звенья манипулятора имеют массы .
Размеры рабочего органа считаются
существенно малыми по сравнению с
остальными линейными размерами
манипулятора. Составим уравнения
движения манипулятора, считая все
элементы абсолютно твердыми телами.
Рука считается однородным стержнем
длиной
.
Размеры рабочего органа считаются
существенно малыми по сравнению с
остальными линейными размерами
манипулятора. Составим уравнения
движения манипулятора, считая все
элементы абсолютно твердыми телами.
Рука считается однородным стержнем
длиной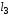 и массой
и массой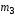 .
Рабочий орган представляет собой
точечную массу
.
Рабочий орган представляет собой
точечную массу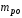 .
.
Кинетическая энергия манипулятора представляет собой сумму кинетических энергий отдельных частей:
 ,
(4.4)
,
(4.4)
где
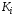 –
кинетическая энергияi-го
звена;
–
кинетическая энергияi-го
звена;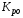 –
кинетическая энергия рабочего органа.
–
кинетическая энергия рабочего органа.
Кинетические энергии для звеньев и рабочего органа равны:
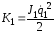 ;
;
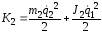 ;
;
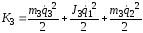 ;
;
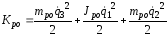 .
.
Моменты инерции для звеньев и рабочего органа равны:
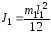 ;
;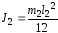 ;
; ;
;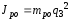 ,
,
где
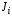 –
момент инерцииi-го звена;
–
момент инерцииi-го звена; –
момент инерции рабочего органа.
–
момент инерции рабочего органа.
Момент
инерции
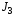 меняется на разных фазах движения из-за
изменения конфигурации манипулятора.
меняется на разных фазах движения из-за
изменения конфигурации манипулятора.
Подставим найденные выражения для кинетических энергий и моментов инерции в уравнение (5.3):

Потенциальная энергия манипулятора равна
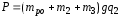 .
.
Для уравнения Лагранжа найдем производные:
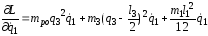 ;
;
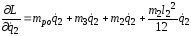 ;
;
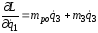 ;
;
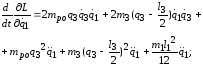
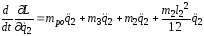 ;
;
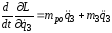 ;
;
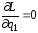 ;
;
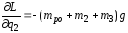 ;
;
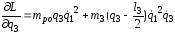 .
.
Подставим найденные производные в уравнение (4.2), произведем необходимые преобразования и получим решение прямой задачи динамики в векторно-матричной форме (4.3):
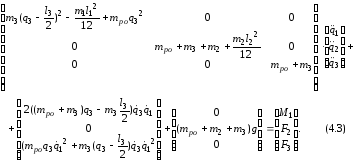
Здесь
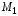 –
момент, развиваемый приводом в первом
сочленении,
–
момент, развиваемый приводом в первом
сочленении,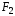 и
и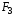 –
силы, развиваемые приводами во втором
и третьем сочленениях. Несмотря на
достаточно простую кинематическую
схему манипулятора, уравнения динамики
являются нелинейными и взаимосвязанными
по координатам
–
силы, развиваемые приводами во втором
и третьем сочленениях. Несмотря на
достаточно простую кинематическую
схему манипулятора, уравнения динамики
являются нелинейными и взаимосвязанными
по координатам и
и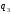 .
Однако движение по координате
.
Однако движение по координате описывается независимым линейным
уравнением.
описывается независимым линейным
уравнением.
4.3. Математическая модель электродвигателя постоянного тока
Математическое описание элементов САУ получают с использованием аналитических и экспериментальных методов. При применении аналитических методов используют известные физические закономерности, описывающие работу элементов и устройств, основу которых составляют дифференциальные уравнения. Далее, в зависимости от требуемой формы представления математического описания САУ, выполняют соответствующие преобразования исходной системы уравнений и приводят описание САУ к виду, удобному для дальнейшего исследования.
Электродвигатель постоянного тока имеет следующие уравнения:
электрической цепи
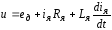 ;
;
механической цепи
 ;
;
момента сопротивления
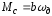 ;
;
момента двигателя
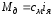 ;
;
э.д.с. двигателя
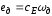 ,
,
где
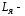 индуктивность
цепи якоря;
индуктивность
цепи якоря;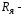 сопротивление
в цепи якоря;
сопротивление
в цепи якоря;
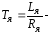 электромагнитная
постоянная времени, характеризует
инерционность электрической части
двигателя;
электромагнитная
постоянная времени, характеризует
инерционность электрической части
двигателя;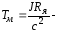 электромеханическая постоянная времени;
электромеханическая постоянная времени;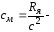 коэффициент
электромагнитного момента двигателя;
коэффициент
электромагнитного момента двигателя; конструктивная
постоянная электродвигателя;
конструктивная
постоянная электродвигателя;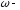 угловая
скорость;
угловая
скорость;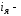 ток
в цепи якоря;
ток
в цепи якоря;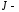 момент
инерции якоря;
момент
инерции якоря;
Двигатель соединяется с нагрузкой через
редуктор с передаточным отношением i.Вращающий момент двигателя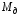 и
его угловую скорость
и
его угловую скорость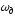 целесообразно привести к выходному
валу редуктора:
целесообразно привести к выходному
валу редуктора:

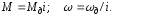
Решая их совместно, получим векторно-матричное уравнение, описывающее электродвигатель постоянного тока в матричном виде:

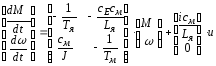 (4.5).
(4.5).
4.4 Математическая модель манипулятора в пространстве состояний
Для всего робота при одновременном выполнении движений по различным степеням подвижности необходимо совместно рассматривать движение манипулятора и системы приводов, включающей двигатели и передачи по всем степеням подвижности. К уравнениям движения манипулятора надо добавить уравнения для системы приводов, связывающие силы и моменты, развиваемые приводами (они стоят в правых частях уравнений движения манипулятора) с управляющими воздействиями, поступающими из системы управления на приводы.
Уравнения, описывающие динамику манипулятора и двигателя, получены выше.
Поскольку подвижные элементы робота считаются жестко связанными с корпусом и валом двигателя, частота вращения двигателя линейно связана с обобщенной скоростью звена. Поэтому в полную ММ “электродвигатель-манипулятор” из системы уравнений, описывающей электродвигатель (4.5), войдет только по одному уравнению, описывающему динамику формирования момента в соответствующем сочленении
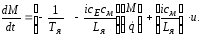
Второе уравнение, описывающее динамику формирования скорости вращения, полностью совпадет с аналогичным уравнением механической основы робота
.
Опишем динамику всей электромеханической системы уравнениями в пространстве состояний.
Введем переменные состояния:
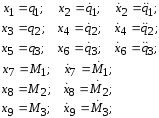
Представим уравнение (4.4) в виде:
 ,
,
где
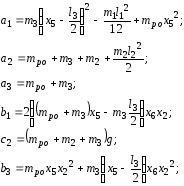
С учетом введенных обозначений система уравнений в пространстве состоя-
ний, описывающая манипулятор, оснащенный электродвигателями постоянно-
го тока, имеет вид:
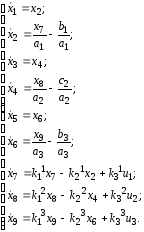 (4.6)
(4.6)
где
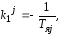
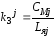 ,
,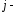 номер
сочленения.
номер
сочленения.
В векторно-матричном виде система уравнений (4.6) записывается :
 (4.7)
(4.7)
Полученная система уравнений, описывающая объект управления в пространстве состояний, имеет девятый порядок. Система обладает существенными нелинейностями, которые наряду с большой размерностью затрудняют синтез. В следующем разделе предлагается метод позволяющий синтезировать дискретно-непрерывную систему управления без необходимости упрощения математической модели, что увеличивает точность позиционирования ПР рабочего органа.
5 Анализ методов синтеза систем управления
