
Дифференциальные уравнения
Основные теоремы дифференциального исчисления.
Теорема Ферма.
![]() непрерывна на
непрерывна на
![]() и дифференцируема на
и дифференцируема на
![]()
![]()
Или ![]()
![]()
![]()
Доказательство.
![]()
![]()
![]()
![]()
![]()
![]()

Теорема Ролля.
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
![]()
Доказательство
Наиб
![]() ,
наим
,
наим
![]() ,
где
,
где
![]()
1)
![]()
![]()
![]()
2)
![]() или
или
![]()
Теорема Лагранжа
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
Теорема Ролля частный случай т.Лагранжа.
Доказательство.
![]()
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Теорема Каши.
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
Доказательство.
![]()
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
![]()

Теорема Лопиталя![]() .
.
![]() ,
,![]() - удовл. т.Каши
- удовл. т.Каши
![]()
Сущ.
 сущ
сущ

Доказательство

![]()
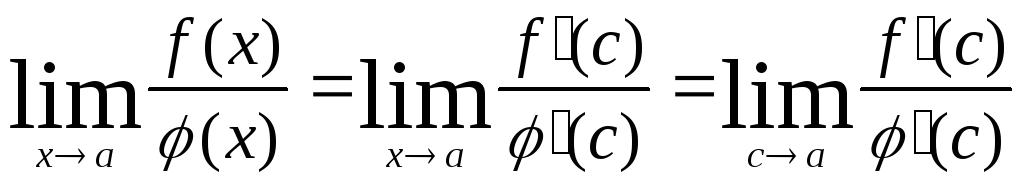
Замечание
Вместо
![]() можно
можно ![]()
Теорема Лопиталя2![]()
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]() непрерывна на
непрерывна на
![]()
диф. на
![]()
![]()
![]()
![]()
Сущ
 сущ
сущ

![]()
Применение дифференциального исчисления к исследованию функций
-
Монотонность
Т1.(необходимые условия монотонности)
![]() - непрерывна и
дифференцируема
- непрерывна и
дифференцируема
Если
![]() возрастает
возрастает
![]()
![]()
Если
![]() убывает
убывает
![]()
![]()
Доказательство
![]()

![]() ч.т.д.
ч.т.д.
Т2.(достаточное условие монотонности)
![]() непрерывна и
дифференцируема
непрерывна и
дифференцируема
![]() возрастает
возрастает
![]() убывает
убывает
Доказательство.
![]()
Уравнение Бернулли.
(1)
![]()
![]()
Решение.
-
Как линейное.
![]()

-
Сводится к линейному
-
разделим на

![]()
Замена
![]()
![]()
![]()
Пример.


Уравнение
![]()
![]()


![]()

![]()


Пример.
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()
![]()
Дифференциальные уравнения высших порядков.
y (n) =f(x,y,y′,…,y(n-1)) (1) если уравнение n-го порядка, то будет n начальных условий.
y(x0)=y0
y′(x0)= y0′ (2) решения (1), удовлетворяющего усл. (2)
y (n-1) (x0)=y0(n-1) назыв. Задачей Коши
Теорема: (о существовании и единственности решения задачи Коши)
f, fy, f′y,…, f′y(n-1) непр. в обл. D M0(x0, y0, y0′,…, y0(n-1))
=> существует единств. Решение
y=φ(x) ур-я (1) удовл-го (2)
(*) y=φ(x1,C1,...,Cn) общее решение (1), если:
1) A) – решение любое С1,..,Сn
2)
![]() (2)
(2)
![]()
![]() !
C1,C20,...Cn0
!
C1,C20,...Cn0
y= φ(C1,C20,...Cn0) - частное решение
Ф(x, y, C1,...,Cn)=0 общий интеграл
Ф(x, y, C10,...,Cn0)=0 частный интеграл
Уравнения 2-го порядка:
y˝=f(x,y,y΄) (1)
система:
y(x0)= y0
y′(x0)= y0′ (2)
 только одна будет под данным углом
прямая (касательная)
только одна будет под данным углом
прямая (касательная)
Уравнение 2-го порядка допускающие понижение порядка.
I. F(x, y′, y′′)=0 - уравнение не содержащее иск. фун-ии y
y′=p(x), y′′=p′
F(x,p,p′)=0
II. F(y, y′, y′′)=0 – уравнение не содерж. произвольной переменной, у – независимая перем-ая
y′=p(y)
y′′x 2= (y′)′x=p′x=p′y *y′x=p′p
F(y,p,p′,p)=0
Например
y*y′′-(y′)²+(y′)³=0
y′=P(y); y′′=p′p
y*P′P-P²+P³=0
P(y*p′-p-p²)=0
-
p=0; y′=0; y=C
-
yP′-P-P²=0
ydp/dy=p-p²
dp/(p- p²)=dy/y
1/(p- p²)=1/p – 1/(p-1)
ln(p)-ln(p-1)=ln(y)+ln(C1)
p/(p-1)=C1y; P-PC1y= –C1y;
P=C1y/(C1y-1); C≠0
-
y′x= C1y/(C1y-1);
dy/dx= C1y/(C1y-1); ∫((C1y-1)/C1y)dy=∫dx;
y-(1/ C1)ln(y)=x+C2
P=0; p=1; y′=1; y=x+ C3; y(0)=-1; y′(0)=0; y=1
Задача о 2-ой космической скорости.
F=mM*k/r²;
-a*m=mMk/ r²
-a=Mk/ r²
v′=-kM/ r²
r ′′=-kM/ r² - уравнение 2го типа
r′=v(r)
r′′=v΄v
v΄v= -kM/ r² - уравнение с разделяющимися переменными
∫vdv= - ∫ (kM/ r²)dr
v²/2=kM/R+C
C=v²/2 - kM/R
v²/2= kM/R+(V0²/2 – kM/R) g=kM/R²
0 r
=> V0²/2 – kM/R0 ; V0² kM/R
V0=√2kM/R
kM/R=gR; V0=√2gR ; R=(40*106)/2π
V0=√2*9,81*40*106)/2π=2*10³√9,81/3,14=11,2*10³(м/с)
Уравнения цепной линии

системы
H=T cosφ; H=T cosφ;
P=T sinφ ; PS=T sinφ;
tgφ=PS/H; P/H=1/a;
y′=s/a
y˝=1/a*S΄x
y˝=(√1+(y΄)²)/a
y′=p(x); y˝=p′; dp/dx=(√1+p²)/a;
p
 ′=(√1+p²)/a;
p(0)=0; ∫dp/(√1+p²)=∫dx/a;
′=(√1+p²)/a;
p(0)=0; ∫dp/(√1+p²)=∫dx/a;
ln 



 p+(√1+p²) =x/a+с с=0
p+(√1+p²) =x/a+с с=0
P+√p²+1=ex/a
p²+1=( ex/a –p)²; 1=e 2x/a -2pe x/a
P=(e2x/a - 1)/2ex/a =(ex/a - e-x/a)/2=sh(x/a)
y′= sh(x/a); y=a*ch(x/a)+C1
y=a*ch(x/a)
Особое решение дифференциальных уравнений.
Это такое решение, в котором нарушается условие единственности.
F(x, y, y′)=0 (1)
y=φ(x) –особое решение {если, через каждую точку кривой φ(x) проходит еще одно решение и эта кривая не принадлежит общему решению}
Огибающая семейство кривых.
Ф(x,y,c)=0 (2) уравнение (2) задает параметрич. семейство, зависящее от параметра С.

Кривая ℓ называется огибающей семейства (2), если в каждой точке кривая ℓ касается одной из кривых семейства, причем в разных точках касается разных точек.
Теорема
Если семейство (2) является общим интегралом уравнения (1), то его огибающая является особым решением уравнения (1), потому что в каждой точке она удовлетворяет уравнению (1).
Док – во:
Для кривой α1 константа С имеет свое значение => для любой точки существует свое значение С.
Возьмем С не константу, а функцию от х,у
Ф=(x,y,c(x,y))=0 (*)
Ф΄x+ Ф΄y*y΄+ Ф΄c(C΄x+ C΄y* y΄)=0 (**)
Ф΄x+ Ф΄y*y΄=0
Из (2) y΄= - Ф΄x/ Ф΄y;
Ф΄c(c(x,y)) ΄x=0, т.к. на огиб. С не явл. константой => (c(x,y))΄x≠0 => Ф΄c=0
Система:
Ф(x,y,c)=0
Ф΄c(x,y,c)=0 (3) система, из которой находиться уравнение огибающей.
Замечание: (3) задает любое С дискриминантные кривые, в том числе и огибающие.
Решение дифференциальных уравнений.
y²(1+y΄²)=R²
1+y΄²= R²/ y²
y΄=±√ (R²/ y²-1); y΄=±(√ (R²- y²))/y
dy/dx=±(√ (R²- y²))/y;
ydy/(√ (R²-
y²))= - +∫dx

- +√ (R²- y²)=x+C;
R²- y²=(x+c)²
(x+c)²+ y²= R²
система
(x+c)²+ y²= R²
2(x+c)=0 (β)
y²= R²
y=±R(γ)
Задача:
Орудие стреляет под углом α к горизонту. Найти семейство траекторий и огибающую этого семейства.
V0 = нач скорость (движение поступательное)
 x=
V0t*cos
α
x=
V0t*cos
α
y= V0t*sin α - gt²/2 – семейство относит. пар-ра α
t=x/ V0t*cos α
y=x tgα - gx²/2V0*1/cos²α
tg α=k; 1/cos²α=tg²α+1=k²+1;
y=kx - g/2V0²( k²+1) x²
g/2V0²=a; k=1/2ax;
 парабола
парабола
система:
y=kx - a(k²+1)x²
0=x - ax²2k
y=1/2a - a(1/4a²x²+1) x²
y=1/2a - 1/4a - ax²
y=1/4a - ax²
Линейные д.у.

Теорема множество решений однородного ур-я (2) образуют линейные пространства
Д-во: L – линейное пр-во
для
![]() элементов
элементов
![]() ,
,
![]() const
const
![]()
![]() (и 8 аксиом)
(и 8 аксиом)
пусть у1,у2 – решение (2)
рассмотрим их лин. комбинацию:

Система функций
![]() называется Л.Н., если равенство
называется Л.Н., если равенство
![]()
выполняется
![]()
![]() Л.З, если
Л.З, если
![]()
![]()
для любых рассматриваемых ф-ций
Теорема 1 Система функций Л.З.
![]() когда одна из них является линейной
комбинацией
когда одна из них является линейной
комбинацией
всех остальных.
![]() - линейно зависима
- линейно зависима
![]()
Д-во:
![]()
![]()
например
![]()
![]()
![]() например
например
![]() является линейной комбинацией
является линейной комбинацией
![]()
Следствие: если система содержит функцию
![]() эта система Л.З.
эта система Л.З.
2 вектора Л.З.
![]() когда они колиниарны
когда они колиниарны
2 функции:
![]() Л.З.
Л.З.
![]() или
или
![]() ,
,
т.е. одна функция линейно выражается через другую
Определитель Вронского

Теорема 2 пусть система ф-ций
![]() Л.З.
Л.З.
![]() их определитель Вронского
их определитель Вронского
![]() ,
т.е.
,
т.е.
![]()
Д-во:
![]()

Теорема 3 пусть
![]() решение ур-я (2)
решение ур-я (2)
![]() или
или
![]()
Д-во: (n=2)
![]()
![]() решения
решения
![]()

Определитель Вронского для системы решений удовлетворяет дифф-му ур-ю :

допустим, при значении
![]()

![]() - Лиувиль
- Лиувиль
Теорема 4 пусть
![]() решения ур-я (2)
решения ур-я (2)
система решений
![]() - Л.Н.
- Л.Н.
![]()
Теорема 5 пусть
![]() Л.Н. решения ур-я (2)
Л.Н. решения ур-я (2)
функция
![]() является общим решением (2)
является общим решением (2)
чтобы выписать общее решение однородного ур-я, нужно найти
n – Л.Н. частных решений
Д-во: 1)
![]() - решение
- решение
![]() - доказано
- доказано
2) при
![]() начальных условиях
начальных условиях
![]() набор констант
набор констант
![]() начальных условиях
начальных условиях
![]()
введем начальное условие:

получим систему n – го
порядка относительно констант
![]()

система (***) имеет единственное решение
![]() ,
т.е. константы определяются единственным
образом.
,
т.е. константы определяются единственным
образом.
Теорема 6
![]() Л.Н. решения ур-я (2)
Л.Н. решения ур-я (2)
![]() - решение (1)
- решение (1)
![]() общее решение неоднородного уравнения
(1)
общее решение неоднородного уравнения
(1)
( здесь
![]() общее решение (2) )
общее решение (2) )
Д-во: 1)
![]() - решение (1)
- решение (1)

![]() - решение (1)
- решение (1)
2) подставим начальные условия:

Уравнения с постоянными коэффициентами
![]()
![]() (2.1) однородное уравнение 2го порядка
(2.1) однородное уравнение 2го порядка
![]() подберем
подберем
![]() так, чтобы
так, чтобы
![]() было решением
было решением

![]()
1)
![]()

2)

Теорема 7 если функция
![]() является решением однородного ур-я (2)
является решением однородного ур-я (2)
![]() тоже являются решениями (2)
тоже являются решениями (2)
Д-во:
![]()
![]()
отделим действительную часть от мнимой:

из Т. следует, что в качестве решения можем брать действительную и мнимую части:

3)
![]() есть только одно решение
есть только одно решение

подберем второе решение, чтобы
![]() не являлось Const
не являлось Const
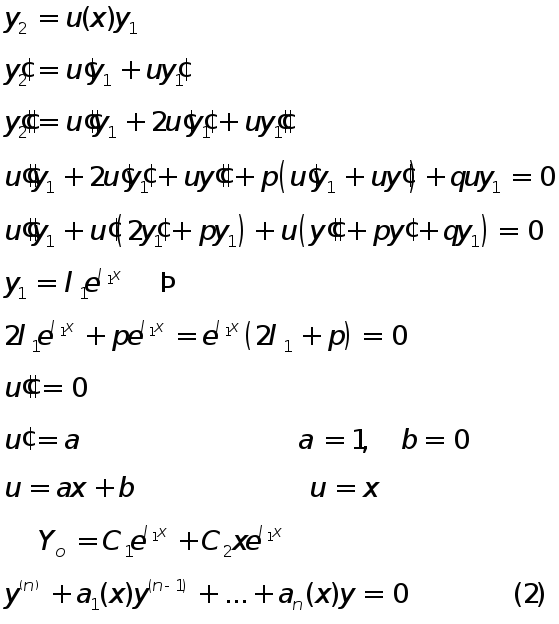
![]() многочлен n-ной степени
многочлен n-ной степени
пусть
![]() - корень уравнения (3) кратности m
- корень уравнения (3) кратности m
ф-ция:
![]() решение (2)
решение (2)
если n - кратный корень, то есть m Л.Н. частных решений.
Решение неоднородного уравнения.
( 1)
1)
(2)
- общее решение (2)
Метод вариации произвольных постоянных.
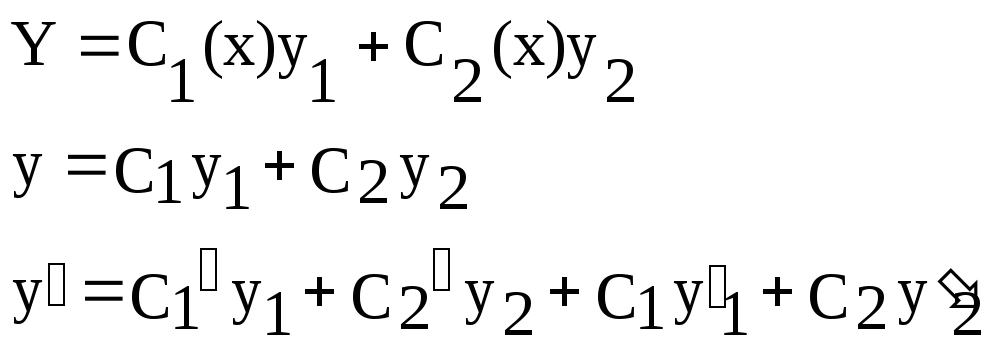
- решение (1) ищем в этом виде.
Пусть
![]() =0
->
=0
->


![]() =
f(x)
=
f(x)
(3) -> единственное решение.
![]() =
0
=
0
 y1
y2
y1
y2
![]() = W(y1,y2)
= W(y1,y2)![]() 0
0
![]()
![]()
В общем виде:
![]()
![]()
Пусть
![]() - общее решение
- общее решение
![]() ,
,
Тогда
![]() - общее решение
- общее решение
![]() ,
,
где
![]()

 (3)
(3)
Пример 1.

Решение.
1)
![]() =
0;
=
0;

2) y =C1(x)cos x + C2(x) sin x



![]()


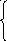
![]()
![]()
y =
![]() cos
x +
cos
x +
![]() sin
x + (
sin
x + (![]() cos
x + tg x sin x).
cos
x + tg x sin x).
Ответ. y =
![]() cos
x +
cos
x +
![]() sin
x + (
sin
x + (![]() cos
x + tg x sin x).
cos
x + tg x sin x).
Решение неоднородного линейного уравнения с постоянными коэффициентами, где правая часть имеет специальный вид.
(![]() 1)
1)
(2)
( 3)
3)
I.
![]() не
корень характеристического уравнения.
не
корень характеристического уравнения.
![]() ищем в виде:
ищем в виде:
![]()
тогда

(*)
II.
![]() или
или
![]() ,
k1
,
k1![]() k2
k2
![]() ищем в виде:
ищем в виде:

(**)
Ш.
![]() =k2=-p/2
=k2=-p/2
![]() ищем в виде:
ищем в виде:

(***)
2) f(x)=
![]() (Pn(x)
cos
(Pn(x)
cos![]() x
+ Qn(x)sin
x
+ Qn(x)sin![]() x)
n- старшая из степеней.
x)
n- старшая из степеней.
I.
![]() +i
+i![]()
![]()
![]() =
=
![]() (Un(x)
cos
(Un(x)
cos![]() x
+ Vn(x)sin
x
+ Vn(x)sin![]() x)
x)
II.
![]() +i
+i![]()
![]()
![]() =x*
=x*
![]() (Un(x)
cos
(Un(x)
cos![]() x
+ Vn(x)sin
x
+ Vn(x)sin![]() x)
x)
Пример 2.
![]()
Решение.
1)

2)
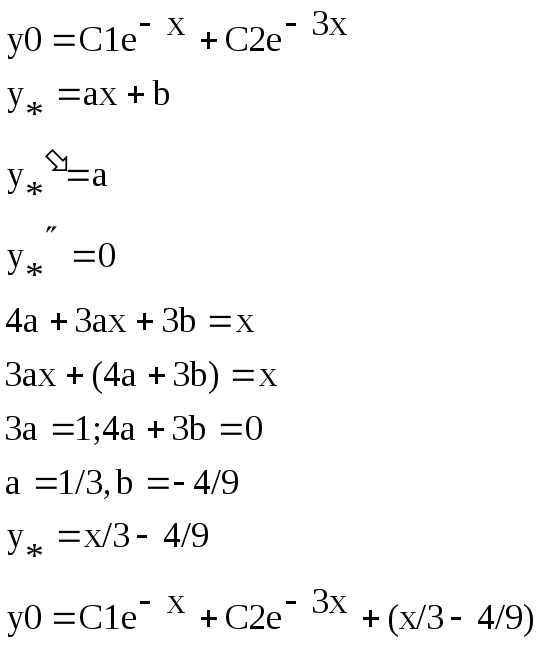
Ответ.
![]() .
.
Пример 3.
![]() Решение.
Решение.
1)

2)

Ответ.
![]()
Пример 4.
![]()
Решение.
1)

2)

Ответ.
![]() .
.
Пример 5.
![]()
1)

2)
![]() =A
cos x+ B sin x
=A
cos x+ B sin x
![]() =-A
sin x+ B cos x
=-A
sin x+ B cos x
![]() =-Acos
x – B sin x
=-Acos
x – B sin x
-Acos x – Bsin x – 2Asin x + 2Bcos x+5Acos x +5Bsin x = 2cos x
cos x(-A+2B+5A)=2cos x +sin x (B+2A-5B)
-A+2B+5A=2
4A+2B=2
2A+2B=1
B=1/5, A=2/5;
y = 2/5 cos x +1/5 sin x
y =
![]()
Ответ. y=![]() .
.
Пример 6.
![]()
1)

2)
![]() =x (Acos 2x + Bsin 2x)
=x (Acos 2x + Bsin 2x)
![]() =(-2Asin
2x+2Bcos 2x)x + Acos 2x+ Bsin 2x
=(-2Asin
2x+2Bcos 2x)x + Acos 2x+ Bsin 2x
![]() =
- 2Asin 2x + 2Bcos 2x + x(-4Acos 2x – 4Bsin 2x) + Acos 2x +Bsin 2x.
=
- 2Asin 2x + 2Bcos 2x + x(-4Acos 2x – 4Bsin 2x) + Acos 2x +Bsin 2x.
-2Asin 2x+ 2B cos 2x + Acos 2x + Bsin 2x = 0
(-2A+B)sin 2x + (2B+A)cos 2x=0.
A=0, B=1/4;
![]() =x(1/4
sin 2x).
=x(1/4
sin 2x).
Y=C1cos 2x + C2 sin 2x+ ¼*x*sin 2x.
Ответ. Y=C1cos 2x + C2 sin 2x+ ¼*x*sin 2x.
Теорема 8.
![]()
![]() решение
решение

![]() решение
решение
 решение
уравнения
решение
уравнения
![]() +
+![]()
Доказательство.
Проверим:

ч.т.д.
Пример 7.
![]()
Решение.
1)

2)
f1(x) = x ,
![]() =Ax+B
=Ax+B
f2(x) = 3![]()
![]()
(A+ C![]() )`
+ 4 (Ax+B+C
)`
+ 4 (Ax+B+C![]() )
= x + 3
)
= x + 3![]()
C![]() +4Ax+4B+4C
+4Ax+4B+4C![]() =x
+3
=x
+3![]()
C=3/5, A=1/4, B=0;
y=C1cos 2x + C2sin 2x + 1/4x+ 3/5![]()
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРОВНЕНИЙ.
(1)

(2)

Т.1
Если система разрешена относительно старших производных, то можно свести к нормальному виду.

Док.
![]()
пусть y=y1, y|=y2,…, y(n-1)=yn
![]()

![]()
Сведение дифференциальных систем уравнений к линейным


![]()
![]() ;
;
![]()
Аналогично
![]()
![]()

 (
(![]() )
)
решение относительно y2,…,yn


Подставим в (![]() )
)
![]()
![]()

y| = x+y+z
z| = 2x-4y-3z
y(0)=0
z(0)=0
y|| = 1+y| +z|
y|| = 1+x+y+z+2x-4y-3z
z=y| -x-y

![]()
K=-1
y0 =e-x(c1+c2x)
2)
y*
Ax+B
![]()
![]()
2A+Ax+B = 5x+1
 A=5
A=5
B=-9

1=c1-9 c1=10
0=-2c1+c2+14 c2=6

![]()
Линейные системы

(1)

X=(x1,…,xn)
![]()

![]()
![]() …
…
![]()
A(t)= ![]()
![]() …
…
![]()
…………………………
![]()
![]() …
…
![]()
![]()
(1)
(2)
![]()
Общее решение однородной системы
![]()
x1,…,xn – частные лин. Независимые решения (2)
С1,…,Сn – произвольные постоянные
О.р. (1):
X=X0+X*
X0- общее решение однородной системы
X*- частные решения (1)


![]()

y|,…,yn
– лин. Независимы =>
![]()
x|,…,xn – решение (2)
x|,…,xn
лин. независимы![]() W(x|,…,xn)
W(x|,…,xn)![]()
Линейные системы с постоянными коэффициентами
(1)
![]()
(2)
![]()
ищем решение (2) в виде
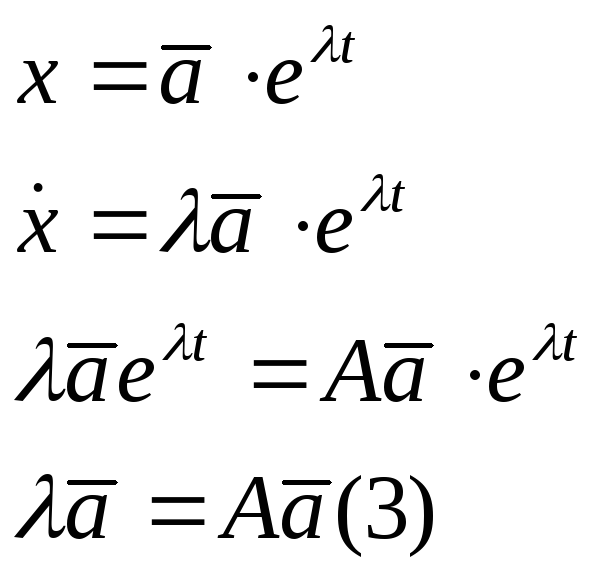
Если
![]() и выполняется (3), то
и выполняется (3), то
![]() называется собственным числом А
называется собственным числом А
![]() - собственным
вектором
- собственным
вектором
![]()
![]()
![]() (4)
(4)
1) (4) имеет n
корней
![]()
=>
![]() ,
j=1,…,n.
,
j=1,…,n.
лин. независимые решения (2)
2) (4) имеет кратные корни.
Пусть
![]() - корень кратности
- корень кратности
![]()
ему соответствуют
собственные векторы
![]()
![]()
2.1) k=m
![]()
лин. независимые решения (2)
2.2) k<m
=> частное решение ищется в виде
![]()


 3 4 -2
3 4 -2
A= 1 0 1
6 -6 5


-1-![]() 4 -2
4 -2
1 -![]() 1
1
6 -6 5-![]()
(-3-![]() )
(
)
(![]() -5
-5![]() +6
+6![]() )
-4(5-
)
-4(5-![]() -6)
-2(-6+6
-6)
-2(-6+6![]() )=0
)=0
-(![]() +3)(
+3)(
![]() 2
-5
2
-5![]() +6
+6![]() )
+8
)
+8![]() +16
+16
(![]() +3)(
+3)(
![]() -2)(
-2)(
![]() -3)
+8(
-3)
+8(![]() -2)=0
-2)=0
![]() =2
=2
![]() 2
-9 +8=0
2
-9 +8=0
![]() =
=![]() 1
1
