2. Кручение бруса с круглым поперечным сечением. Напряжение в брусе круглого поперечного сечения. Условия прочности. Определение угла закручивания. Условие прочности

Под кручением понимается такой вид нагружения, когда в поперечных сечениях бруса возникают крутящие моменты. Крутящий момент будем считать положительным, если, глядя со стороны внешней нормали к сечению, наблюдатель видит его направление против часовой стрелки (рис.3.9).

Рис. 3.9

Нанесем на боковую поверхность скручиваемого бруса ортогональную сетку (рис. 3.10).

Рис. 3.10

После закручивания прямоугольники перекашиваются. При кручении происходит поворот одного сечения относительно другого. Сформулируем гипотезы, которые положим в основу дальнейших выводов.

1. Сечения, плоские до закручивания, остаются плоскими, и после закручивания.

2. Радиусы, проведенные в любом поперечном сечении, в процессе кручения не искривляются.

Двумя поперечными и кольцевым сечением выделим элемент длиною (рис. 3.11).

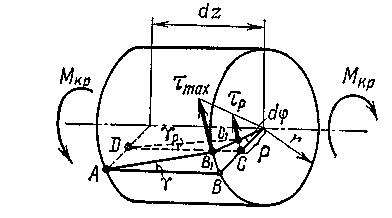
Рис. 3.11

Для удобства левое его сечение будем считать неподвижным. Поворот правого сечения относительно левого равен . Образующаяотклонится на малый уголи перейдет в положение. Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством.

Для произвольного волокна, отстоящего от центра на расстоянии , будем иметь. На основании закона Гука при сдвиге для двух указанных точек можно записать

(3.6)

, (3.7)

где — относительный угол закручивания.

Из формулы видно, что напряжения меняются по сечению по линейному закону пропорционально радиусу. Графически этот закон представлен на рис. 3.12,а. Для стержня кольцевого сечения закон распределения касательных напряжений показан на рис. 3.12,б.

Рис. 3.12

Элементарные силы создают крутящий момент

,

—полярный момент инерции.

Откуда ,

(3.8)

Подставляя в формулу (3.7) полученное выражение (3.8) окончательно получим

(3.9)

Мы получим формулу для определения в любой точке поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле

, (3.10)

где — полярный момент сопротивления.

Взаимный угол поворота двух сечений расположенных на расстоянии равен(т.к.).

С учетом (3.8) получим .

Абсолютный угол закручивания равен

(3.11)

Если —const, то

(3.12)

Условия прочности и жесткости при кручении имеют вид

(3.13)

(3.14)

Вычислим полярные моменты инерции и сопротивления для круга и кольца. По определению их значения определяются выражениями

, .

Вырежем тонкое кольцо (рис.3.13).

Рис. 3.13

Его площадь . Подставляяв интервал. После вычисления интеграла получим:,.

Для кольцевого сечения (рис.3.14) .

Рис. 3.14

Пусть , тогда,.