
- •Введение
- •Глава 1. Основы сопротивления материалов
- •Предмет «Сопротивление материалов»
- •Объект курса
- •Внешние силы
- •Основные понятия и гипотезы (допущения)
- •Внутренние силы и их определение. Метод сечений
- •Эпюры внутренних усилий
- •Понятие о напряжении и напряженном состоянии
- •Понятие о деформации тела и о деформации физических точек
- •Глава 2. Растяжение, сжатие бруса
- •Напряжения и деформации при растяжении и сжатии. Закон Гука
- •2.6. Диаграмма сжатия
- •2.7. Расчеты на прочность при растяжении (сжатии)
- •Глава 3. Сдвиг и кручение стержней
- •3.1. Понятие о чистом сдвиге. Напряжения и деформации при сдвиге. Закон Гука
- •Практический расчет соединений работающих на сдвиг
- •Кручение бруса с круглым поперечным сечением. Напряжение в брусе круглого поперечного сечения. Условия прочности. Определение угла закручивания. Условие прочности
- •Кручение бруса прямоугольного поперечного сечения
- •Потенциальная энергия бруса при кручении
- •Кручение бруса круглого поперечного сечения за пределом упругости
- •Глава 4. Геометрические характеристики плоских сечений
- •Основные понятия
- •Статические моменты сечения
- •Моменты инерции сечения. Зависимость между моментами инерции при параллельном переносе осей
- •Зависимость между моментами инерции сечения при повороте осей. Главные оси и главные моменты инерции
- •Глава 5. Изгиб
- •5.1. Основные понятия
- •5.2. Дифференциальные зависимости между и
- •5.3. Напряжения в брусе при чистом изгибе
- •5.4. Напряжения при поперечном изгибе
- •5.5. Чистый косой изгиб
- •Внецентренное растяжение и сжатие
- •Глава 6. Перемещения при изгибе
- •6.1. Метод Мора для определения перемещений
- •6.2. Способ Верещагина
- •Глава 7. Статически неопределимые стержневые системы
- •7.1. Введение
- •7.2. Классификация стержневых систем. Системы статической неопределимости
- •7.3. Метод сил. Выбор основной системы
- •7.4. Канонические уравнения метода сил
- •7.5. Использование свойств симметрии при раскрытии статической неопределенности
- •7.6. Определение перемещений в статически неопределимых системах
- •Глава 8. Устойчивость равновесия деформируемых систем
- •8.1. Основные понятия
- •8.2. Дифференциальное уравнение стержня потерявшего устойчивость
- •8.3. Задача Эйлера об устойчивости шарнирно опертого стержня сжатого силой р
- •8.4. Зависимость критической силы от условий закрепленного стержня
- •8.5. Пределы применимости формулы Эйлера
- •8.6. Практический метод расчета стержней на устойчивость
- •Глава 9. Элементы теории напряженного и деформированного состояния
- •9.1. Основные понятия
- •9.2. Напряжения на наклонных площадках
- •9.3. Главные оси и главные напряжения
- •9.4. Круговая диаграмма напряженного состояния
- •9.5. Экстремальные касательные напряжения
- •9.6. Октаэдрические площадки. Октаэдрические напряжения
- •9.7. Деформированное состояние
- •9.8. Формулы обобщенного закона Гука
- •Глава 10. Критерии пластичности и разрушения
- •10.1. Постановка вопроса
- •10.2. Условия пластичности и разрушения
- •10.3. Теория пластичности и разрушения Мора
- •Глава 11. Прочность материалов при циклически изменяющихся напряжениях
- •11.1. Понятие об усталостной прочности
- •11.2. Виды циклов напряжений
- •11.3. Предел выносливости
- •11.4. Диаграмма предельных амплитуд
- •11.5. Факторы, влияющие на усталостную прочность
- •11.5.1 Концентрация напряжений
- •11.5.2 Масштабный эффект
- •11.5.3 Влияние качества обработки поверхности
- •11.6. Расчет на прочность при переменных напряжениях
11.4. Диаграмма предельных амплитуд
Для построения
диаграммы предельных амплитуд необходимо
иметь пределы выносливости при различных
значениях параметра “![]() ”
(коэффициент асимметрии). Введение
”
(коэффициент асимметрии). Введение![]() значительно усложняет эксперимент,
т.к. теперь уже необходимо иметь несколько
десятков образцов, каждый десяток из
которых испытывается при
значительно усложняет эксперимент,
т.к. теперь уже необходимо иметь несколько
десятков образцов, каждый десяток из
которых испытывается при![]() .
Задавая постоянное значение
.
Задавая постоянное значение![]() ,
находим путем последовательных испытаний
образцов такое наибольшее значение
амплитуды, при котором материал способен
еще выдержать неограниченное число
циклов. В результате испытаний одного
десятка образцов получаем одну точку
на диаграмме предельных амплитуд.
Произведя испытания следующей группы
образцов, мы получаем еще одну точку и
т.д. (рис.11.7).
,
находим путем последовательных испытаний
образцов такое наибольшее значение
амплитуды, при котором материал способен
еще выдержать неограниченное число
циклов. В результате испытаний одного
десятка образцов получаем одну точку
на диаграмме предельных амплитуд.
Произведя испытания следующей группы
образцов, мы получаем еще одну точку и
т.д. (рис.11.7).
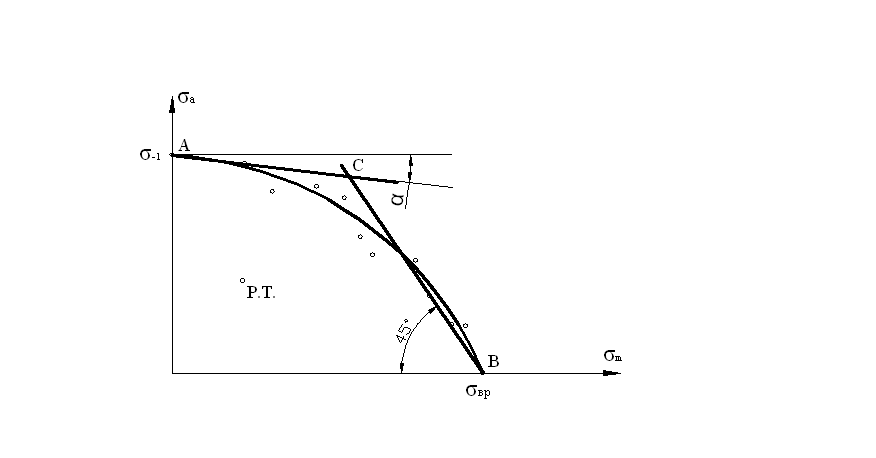
Рис. 11.7
Смысл диаграммы
предельных амплитуд очевиден. Пусть
цикл характеризуют напряжения
![]() и
и![]() ,
которые будем рассматривать как
координаты рабочей точки. Нанеся рабочую
точку на диаграмму, мы можем судить о
прочности образца. Если рабочая точка
располагается ниже предельной кривой,
то образец выдержит бесконечно большое
число циклов (не менее базового). Если
Р.Т. находится выше кривой, то образец
разрушится при каком-то числе циклов,
меньшем базового.
,
которые будем рассматривать как
координаты рабочей точки. Нанеся рабочую
точку на диаграмму, мы можем судить о
прочности образца. Если рабочая точка
располагается ниже предельной кривой,
то образец выдержит бесконечно большое
число циклов (не менее базового). Если
Р.Т. находится выше кривой, то образец
разрушится при каком-то числе циклов,
меньшем базового.
Построение
диаграммы предельных амплитуд![]() очень
трудоемко, поэтому ее часто схематизируют
отрезками прямых. Точка
очень
трудоемко, поэтому ее часто схематизируют
отрезками прямых. Точка![]() отражает соответствующее испытание
образцов при симметричном цикле. Точка
отражает соответствующее испытание
образцов при симметричном цикле. Точка![]() соответствует
статическому испытанию образцов. Для
хрупких материалов она определяется
по пределу прочности
соответствует
статическому испытанию образцов. Для
хрупких материалов она определяется
по пределу прочности![]() .
Для пластичных материалов ограничение
может быть как по пределу текучести
.
Для пластичных материалов ограничение
может быть как по пределу текучести![]() ,
так и пределу прочности
,
так и пределу прочности![]() .
.
Для построения
левой части диаграммы нужна еще хотя
бы одна точка, например, для пульсационного
цикла, либо знать угол
![]() наклона прямой. Введем понятие углового
коэффициента
наклона прямой. Введем понятие углового
коэффициента![]() =
=![]() .
Опытами доказано, что значение углового
коэффициента для углеродистых сталей
лежит в пределах 0,1÷0,2 и для легированных
0,2÷0,3.
.
Опытами доказано, что значение углового
коэффициента для углеродистых сталей
лежит в пределах 0,1÷0,2 и для легированных
0,2÷0,3.
Таким образом,
уравнение левой прямой имеет вид
![]() .
Правая часть диаграммы аппроксимируется
прямой, проходящей через точку
.
Правая часть диаграммы аппроксимируется
прямой, проходящей через точку![]() и составляющей угол 45
и составляющей угол 45![]() с осями
с осями![]() и
и![]()
![]()
Следовательно,
при схематизации диаграмма предельных
амплитуд, заменяется двумя прямыми
![]() и
и![]() .
.
Построенная
диаграмма пока не позволяет рассчитывать
детали на прочность, т.к. усталостная
прочность зависит еще от многих факторов.![]()
11.5. Факторы, влияющие на усталостную прочность
11.5.1 Концентрация напряжений
Концентрацией называют явление скачкообразного увеличения напряжений вблизи резких смен формы детали, отверстий, выточек (Рис. 11.8)

Рис. 11.8
Мерой концентрации является теоретический коэффициент концентрации напряжений равный:
![]() при растяжении,
изгибе,
при растяжении,
изгибе,
![]() при кручении,
при кручении,
![]() —так называемое
номинальное напряжение, определяемое
по формулам сопротивления материалов,
—так называемое
номинальное напряжение, определяемое
по формулам сопротивления материалов,
![]() —
наибольшее местное напряжение. Данные
о теоретическом коэффициенте концентрации
напряжений приводятся в справочниках
по машиностроению. Концентрация
напряжений оказывает на прочность
детали различное влияние в зависимости
от свойств материала и условий нагружения.
Поэтому вместо теоретического коэффициента
концентрации напряжения
—
наибольшее местное напряжение. Данные
о теоретическом коэффициенте концентрации
напряжений приводятся в справочниках
по машиностроению. Концентрация
напряжений оказывает на прочность
детали различное влияние в зависимости
от свойств материала и условий нагружения.
Поэтому вместо теоретического коэффициента
концентрации напряжения![]() вводят эффективный коэффициент
концентрации напряжений
вводят эффективный коэффициент
концентрации напряжений![]() и
и![]() .
.
Для симметричного цикла эффективный коэффициент концентрации напряжений определяют отношением
 ,
,
где
![]() — пределы выносливости гладкого образца,
— пределы выносливости гладкого образца,
![]() —пределы
выносливости подсчитанных по номинальным
напряжениям для образцов, имеющих
концентрацию напряжения, но такие же
размеры поперечного сечения как и у
гладкого образца.
—пределы
выносливости подсчитанных по номинальным
напряжениям для образцов, имеющих
концентрацию напряжения, но такие же
размеры поперечного сечения как и у
гладкого образца.
![]() определяют по таблицам.
определяют по таблицам.
В тех случаях,
когда нет экспериментальных данных, по
прямому определению
![]() и
и![]() прибегают
к приближенным оценкам. Например, по
формуле
прибегают
к приближенным оценкам. Например, по
формуле
![]()
![]() —коэффициент
чувствительности материала к концентрации
напряжений. Он зависит в основном от
материала. Для конструкционных сталей
—коэффициент
чувствительности материала к концентрации
напряжений. Он зависит в основном от
материала. Для конструкционных сталей
![]() .
.
