Раздел 2. Метод координат на плоскости

Изучая элементарную геометрию в объеме школьной программы, вы могли обратить внимание на одно важное обстоятельство: способы доказательств различных теорем, по своему содержанию часто довольно близких друг к другу, совершенно различны и мало связаны друг с другом. Например, сравните, приведенные в школьном учебнике, доказательства следующих теорем:

1. Три медианы треугольника пересекаются в одной точке.

2. Три высоты треугольника пересекаются в одной точке.

3. Три биссектрисы внутренних углов треугольника пересекаются в одной точке.

Доказав одну из этих теорем, мы ничего не приобретаем в смысле указания на то, как приступить к доказательству следующей. Ясно, что при этих условиях решение геометрических задач представляет громадные трудности и требует большого искусства геометров. Из истории развития математики известно, что в XVII веке возникла потребность в создании такого общего метода в геометрии, который был бы одинаково пригоден для решения самых разнообразных задач и для исследования самых разнообразных кривых. Именно таким методом является метод координат.

Независимо друг от друга основы аналитического метода были открыты в 1636–1637 гг. французскими математиками Пьером Ферма (1601–1665) и Рене Декартом (1596–1650). Распространение методов аналитической геометрии на пространственные образы было сделано значительно позже французским математиком Клеро (1713–1765).

Теперь переходим к систематическому изучению аналитического метода. Основная наша задача состоит в том, чтобы научиться составлять уравнения различных линий и использовать их при решении геометрических задач.

Тема 2.1. Аффинная система координат. Аффинные задачи

Литература: [1], гл. 3, §1, стр. 55–58; [3], гл. 1, §2, стр. 16–17; [4], гл. 6, §23, стр. 189–203.

Основные определения, теоремы и формулы

Тройка, состоящая из точки O и базиса , называетсяаффинной системой координат на плоскости и обозначается символом: Oили (O,) (рис. 11). Вектор(рис. 12) называетсярадиус-вектором точки M (относительно точки O).

Если , то числаиназываютсякоординатами точки M в системе координат O,. Числоназываетсяабсциссой точки M, а число –ординатой; пишут M(,). Заметим, что,.

ПустьA и B – две точки плоскости, а – некоторое действительное число, причем≠–1. Говорят, что точкаM делит (направленный) отрезок в отношении λ, если . При этом отношениеназывают отношением трех точекA, B и M (или простым отношением этих точек) и пишут: =(AB,M).

Координаты точкиM, делящей направленный отрезок в данном отношениивыражаются через соответствующие координаты концов отрезка по следующим формулам:.

Вопросы для повторения.

1. Что такое аффинная система координат? Как она задается? Как обозначается?

2. Как определяются координаты точки в аффинной системе координат?

3. Докажите, что если на плоскости задана аффинная система координат, то между точками плоскости и упорядоченными парами действительных чисел устанавливается взаимно однозначное соответствие.

4. Покажите на примерах как построить точку по ее заданным координатам в аффинной системе координат.

5. Докажите, что каждая координата вектора равна разности соответствующих координат конца и начала вектора.

6. Точка Mделит направленный отрезок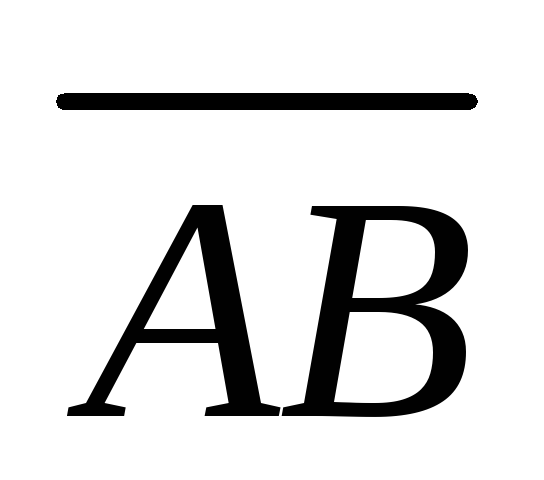в отношении. В каком отношении точкаMделит отрезок?

7. В каком отношении делится направленный отрезок 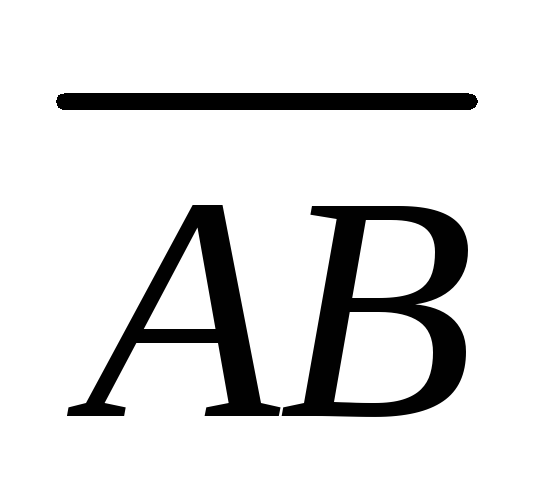: а) точкойA; б) точкойB; в) серединойMотрезкаAB?

8. Как выражаются координаты точки С, делящей отрезокАВв отношении, через соответствующие координаты концов отрезка?

9. Покажите, что для любого действительного числа , отличного от –1 , на прямойАВсуществует одна и только одна точкаМ, делящая направленный отрезокАВв отношении.

8. Какие значения принимает λ, когда точка МпрямойМ₁М₂лежит на: а) отрезкеМ₁М₂, б) луче,М₁М₂; в) луче, дополнительном к лучуМ₁М₂?

9. Точка Мделит направленный отрезокМ₁М₂в отношении λ. Как перемещается точкаМна прямойМ₁М₂, если известно, что:

а) λ →0; б) λ→+; в) λ→ –; г) λ→ –1.

1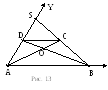0. Постойте точкиР₁,Р₂,Р₃, делящие данный направленный отрезокв отношении: 1)₁= 3, 2)₂= –2, 3)₃=–.

Пример1. В трапецииABCDнижнее основаниеABв три раза больше верхнего основанияCD. Принимая за начало координат точкуA, за положительное направление оси абсцисс – направление боковой стороныAD, а стороныABиAD– за единичные отрезки на этих осях, найти координаты вершин трапеции, а также координаты точкиOпересечения ее диагоналей и координатыS пересечения ее боковых сторон (Рис. 13).

Решение.По условию задачи аффинная система координат задана точкойAи векторами и . ПоэтомуA(0,0),B(1,0),D(0,1). Так как =, то +=+. Значит,C(;1).

Замечаем, что гомотетия с центром в точке Sи коэффициентом 3 переводит отрезокDCв отрезокAB. Следовательно,, т. е. точкаSделит отрезокADв отношении, и,;.

Найдем теперь координаты точки Oв системе координат (A, , ). Для этого необходимо найти разложение вектора по векторам и .

Так как ∆AOBподобен ∆COD, и коэффициент подобия равен 3, то =3. Записав это равенство в координатах, получим систему двух линейных уравнений с двумя неизвестными. Решая которую, получим:

;;.

Пример2. Найдите аффинные координаты точки, симметричной точкеотносительно точки.

Решение.Пусть– искомая точка. Тогда =. Переходя к координатам, получим,. Отсюда,.

Задачи

1. В заданной системе координат (O, 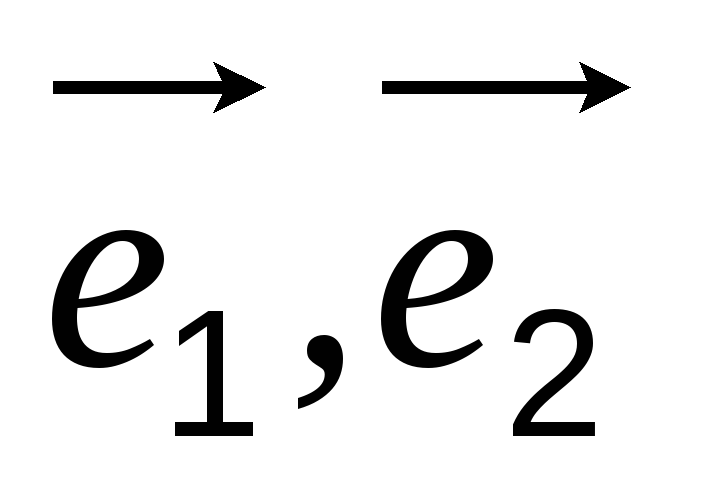) построить следующие точки:A(−1,0),B(−2,1),C(1,1),D(−3,2),E(0, −2),R(3, −3).

2. Найти координаты середин отрезков A₁B₁,A₂B₂,A₃B₃, если:

A₁(−1,5), B₁(−3,3), A₂(0,4), B₂(3,2), A₃(−2,6), B₃(1,4).

3. На прямой отмечена последовательность точек A₁, A₂, A₃, A₄, A₅, A₆ так, что A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅,A₆. Зная координаты точекA₂(2,5) иA₃(−1,7), определить отношения, в которых точкиA₁,A₃,A₄,A₆делят отрезокA₂A₅, а также координаты этих точек.

4. По координатам трех вершин A, B, Cпараллелограмма вычислить координаты четвертой вершины: 1)A(1,4),B(3, −1),C(0,2); 2)A(−1,0),B(2,1),C(4, −1).

5. Доказать, что точки A, BиCпринадлежат одной прямой и выяснить, какая из трех точек лежит между двумя другими, если: 1)A(2,1),B(0,5),C(4, −3); 2)A(−1,0),B(1, −2),C(3, −4).

6. Точки KиM – середины сторонBCиCDпараллелограммаABCD. Найти координаты вершин параллелограмма в репере (A, K, M).

7. Найти координаты точки пересечения диагоналей четырехугольника ABCDс вершинамиA(−2,14),B(4, −2),C(6, −2),D(6,10).

8. Заполните таблицу:

На геометрическом языке	На языке координат
1. Дана точка A
2. Данные точки A, B, C: лежат на одной прямой; не лежат на одной прямой; Cсередина отрезкаAB; Точка Cделит направленный отрезокAB в отношении λ
3. A, B, C, D– вершины параллелограмма
4. A, B, C, D– вершины трапеции с основаниямиABиCD