Задачи повышенной трудности

1. Дана окружность и некоторая точка A, лежащая в плоскости окружности. ОтрезокAN, гдеN– произвольная точка окружности, точкойMразделен в постоянном отношении. Найти множество точекM.

2. В прямоугольной декартовой системе координат даны уравнения двух пересекающихся окружностей:

Вывести формулу для вычисления угла между этими окружностями.

Домашнее задание

2. Написать уравнение окружности радиуса 5, касающейся прямых, заданных уравнениями 3x+4y–10=0, 5x–12y+26=0.

3. Написать уравнение окружности, проходящей через точки A(2,3) иB(3,6) и касающейся прямой, заданной уравнением

2x+y–2=0.

4. Найти координаты центра и радиус окружности, которая касается оси абсцисс и двух окружностей, заданных уравнениями x²+y²+6x+5=0,x²+y^2–6x+8=0.

5. Составить уравнение окружности, которая касается прямых y=0,y=2xи проходит через точкуA(2,1).

Тема 3.2. Эллипс

Литература: [1], гл. 6, § 2–4, стр. 119–129; [7], гл. 4, § 27, стр. 91–95.

Основные определения, теоремы и формулы

Если оси прямоугольной декартовой системы координат выбраны так, как показано на рисунке 26,то в этой системе координат уравнение эллипса имеет вид:, где– большая,– малая полуоси эллипса. Это уравнение называется каноническимуравнением эллипса. Фокальные радиусыr₁=F₁Mиr₂=F₂MточкиМ(х,y) эллипса вычисляются по формулам:r₁=a+x,r₂=a–x, гдес=F₁F₂. Числа,иcв рассматриваемом случае связаны соотношением:.

Число =, т. е. отношение расстояния между фокусами к длине большой оси называетсяэксцентриситетом эллипса.

Уравнения: (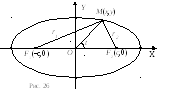0)являются параметрическими уравнениями эллипса, где t – величина угла между осью ОХ и прямой ОМ, соединяющей центр эллипса с его точкой.

Если фокусы эллипса расположены на оси ОY, то вид уравнения эллипса не меняется, но в этом случае > и с=. Эксцентриситет такого эллипсавычисляется по формуле: =.

Примеры решенных задач

Пример 1. Дано уравнение эллипса 25x²+169y²=4225. Вычислить длину его полуосей, найти координаты фокусов, эксцентриситет. Найти фокальные радиусы точкиМ()и точки эллипса, расстояние которых до левого фокусаF₁равно 14.

Решение: Разделив обе части данного уравнения на 4225, получим каноническое уравнение эллипса=1, откуда=169,b²=25. Значит, длины полуосей равны соответственно=13,b=5. Тогдас==12 иF₁(0,–12),F₂(0,12). Эксцентриситет эллипса:=.

Точка М() лежит на эллипсе. По известным формулам найдем ее фокальные радиусы:

r₁=13+22,r₂=13–=13–.

Так как расстояние от искомой точки до левого фокуса равно 14, то ее абсциссу можно найти из уравнения:

14=13+x,x=.

Подставляя найденные значения xв уравнение эллипса, найдем ординаты точек:

y==

Следовательно, условию задачи удовлетворяют две точки, имеющие следующие координаты:

() и ().

Пример 2.Написать уравнение касательной к эллипсу, параллельной прямой.

Решение: Искомая касательная параллельна данной прямой, следовательно, ее уравнение имеет вид. ОпределимСиз условия касания прямой эллипса.

Прямая касается эллипса, если она пересекает ее в двух совпавших точках.

Общие точки прямой и эллипса найдем из системы уравнений:

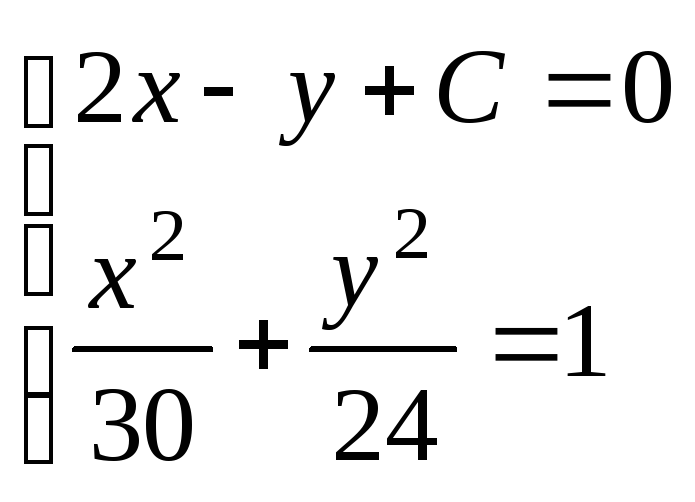
Из первого уравнения . Подставляя найденное выражение во второе уравнение системы, получим квадратное уравнение относительно:

.

Это уравнение имеет равные корни тогда и только тогда, когда его дискриминант равен нулю, то есть.

.

Следовательно, условию задачи удовлетворяют две касательные: .

Задачи

1. Цилиндр, поперечное сечение которого есть круг радиуса 10, пересечен плоскостью, образующей с осью цилиндра угол . Найдите величину полуосей эллипса, получающегося в сечении.

2. Вершина треугольника, имеющего неподвижное основание, перемещается так, периметр постоянен. Найдите траекторию движения вершины при условии, что основание треугольника равно 24, а периметр равен 50.

3. Наименьшее расстояние от Земли до Солнца равно приблизительно 147500000 км, а наибольшее 152500000 км. Найти большую полуось и эксцентриситет орбиты Земли.

4. На прямой l, уравнение которой в репере :, найти точку, сумма расстояний от которой до точекА(–3,0) иВ(5,0) равна 10.

5. Как расположены относительно эллипса точкиA(7, 6),B(5, –4) ,C(–4, 5)?

6. Вывести условие, при котором прямая касается эллипса

7. Доказать, что произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.

8. Доказать оптическое свойство эллипса: всякая касательная к эллипсу образует равные углы с фокальными радиусами точки прикосновения.

9. На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его центр.