Тема 1.6. Применение векторов к решению задач

школьного курса геометрии

Литература: [2], гл. 1, § 10, стр. 42–45; [19], гл. 1, § 1.6, стр. 86–105.

Основные сведения

Векторная алгебра может быть весьма успешно использована при решении широкого класса содержательных геометрических (аффинных и метрических) задач. Аффинные задачихарактеризуются тем, что все участвующие в них объекты и отношения определяются отношением отрезков, площадей, параллельностью. Вметрическихже задачах – длинами отрезков, величинами углов.

Как правило, векторное решение геометрической задачи позволяет автоматически, или после несложного анализа полученных формул и уравнений, сделать интересные обобщения доказываемых геометрических фактов.

Алгоритм применения векторовпри решении геометрических задач состоит из следующих этапов:

1. Выясняем, является ли рассматриваемая задача аффинной или же метрической.

2. Если задача аффинная, то, как правило, выбираем произвольный базис или вводим в рассмотрение наименьшее количество векторов, через которые можно выразить все интересующие нас векторы. Если же задача метрическая, то, как правило, выбираем ортонормированный базис.

3. Все, что дано в задаче, записываем с помощью векторов.

4. Все, что необходимо найти или доказать, записываем с помощью векторов.

5. С помощью алгебраических преобразований из того, что дано, получаем, что необходимо.

Из приведенного алгоритма видно, что если задачу можно перевести на язык векторов, то она решается с помощью векторов. И для успешного использования векторной алгебры к решению геометрических задач необходимо уметь переводить геометрические факты на язык векторов или на язык координат.

Ниже, в таблице, приведены часто встречающиеся примеры.

На языке геометрических фактов	На языке векторов	На языке координат векторов
Прямые ипараллельны.	Векторы иколлинеарны или=t(здесьи- направляющие векторы прямыхисоответственно)	Координаты векторов ипропорциональны, т.е..
Точки А, ВиС лежат на одной прямой.		Координаты векторов ипропорциональны, т.е. .
Точка Слежит между точкамиА иВ.	, <<	Координаты векторов ипропорциональны, т.е. .
Точки АиВсимметричны относительно точкиО.	или	Соответствующие координаты векторов иравны или соответствующие координаты вектора вдвое больше соответствующих координат вектора .
Угол между прямыми и: прямой; острый; тупой;	; ; ;	Если координаты векторов заданы в ортонормированном базисе: 1); 2); 3).

Задание: Для ускорения усвоения этого метода рекомендуем после решения каждой из рассматриваемых задач продумать, какая информация, чем была заменена в процессе работы, и продолжить заполнение таблицы.

Пример 1. Доказать, что медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делятся ею в отношении 2:1, считая от вершины.

Решение. Пусть медианыADиBE пересекаются в точкеО. Докажем, что третья медианаСМтоже проходит через точкуО. Из приведенной выше таблицы видно, что это все равно, что доказать коллинеарность векторови. Эта задача аффинная.

Пусть =,=. Замечаем, что векторы иможно выразить через векторыи:

,.

Так как , то,.

Аналогично, , поэтому:

, .

Найдем вектор . С одной стороны:

.

С другой стороны:

.

Значит, .

Так как векторы илинейно независимы, то отсюда:

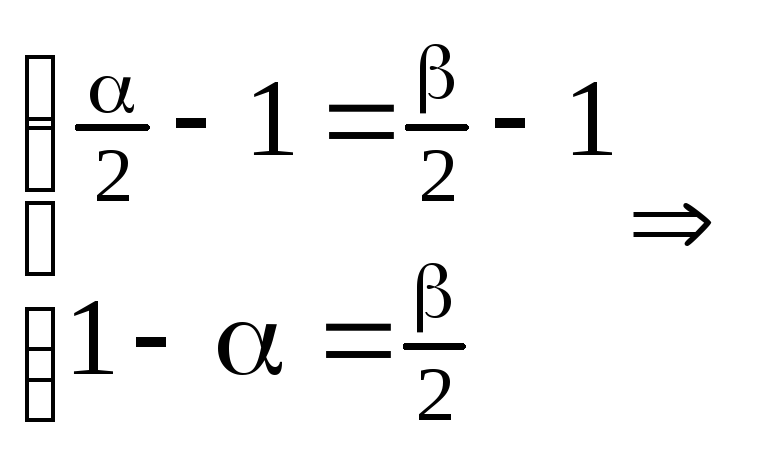
Значит, ,,.

Сравнив векторыи, заключаем:.

Следовательно, третья медиана СМ тоже проходит через точку О.

Пример 2. Доказать, что прямые, содержащие высоты треугольника пересекаются в одной точке.

Решение. Пусть высотыАDиВНпересекаются в точкеО(Рис. 10). Обозначим, ,.Тогда,,.

, то есть, ., т.е. .

Вычтя из первого подчеркнутого равенства второе, получим , т.е.или. Следовательно,перпендикулярноЗначит, и третья высота треугольника проходит так же через точкуО.

Задачи

1. С помощью векторов докажите следующие утверждения: а) если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник – параллелограмм; б) сумма квадратов длин диагоналей параллелограмма равна сумме квадратов всех его сторон; в) диагонали ромба взаимно перпендикулярны; г) средняя линия треугольника параллельна основанию и длина ее равна половине длины основания.

2. Доказать, что в треугольнике ABCугол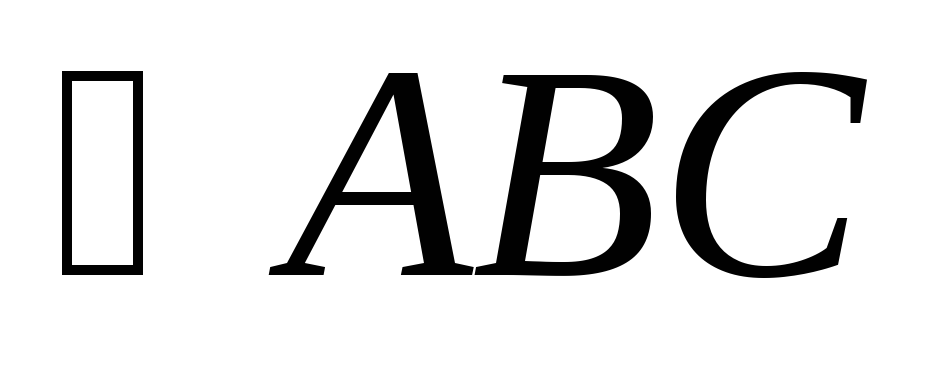прямой тогда и только тогда, когдаAC² =AB² +BC².

3. Доказать, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин ее непараллельных сторон, сложенной с удвоенным произведением длин оснований.

4. В кубе найти величину угла: а) между диагональю и скрещивающейся с ней диагональю грани; б) между скрещивающимися диагоналями соседних граней; в) между диагональю куба и пересекающейся с ней диагональю грани.

5. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей и учетверенного квадрата расстояния между серединами этих диагоналей (теорема Эйлера).

6. Доказать, что в правильном тетраэдре противоположные ребра взаимно перпендикулярны.

7. Доказать, что в четырехугольнике ABCDимеет место равенство: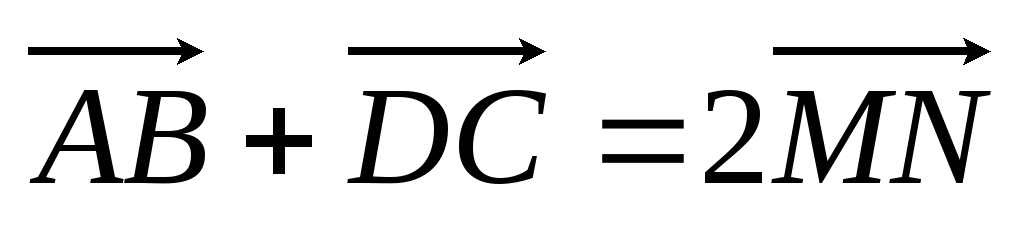, гдеM,N– соответственно середины сторонADиBC. Пользуясь этим равенством, докажите, что средняя линия трапеции (треугольника) параллельна основаниям (основанию) и равна их (ее) половине.