Тема 3.4.Парабола

Литература: [1], гл. 6, §1, стр. 114–119; [7], гл. 4, § 29, стр. 100–103.

Основные сведения

Параболой называется множество всех точек плоскости, расстояние от каждой из которых до данной точки F равно расстоянию до данной прямой d, не проходящей через точку F (Рис. 28). Точка F называется фокусом параболы, а прямая d – директрисой.

Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается через p.

Уравнение называетсяканоническим уравнением параболы.

Точка пересечения параболы со своей осью симметрии называется вершиной параболы.

Задачи

1. Написать уравнение параболы в репере 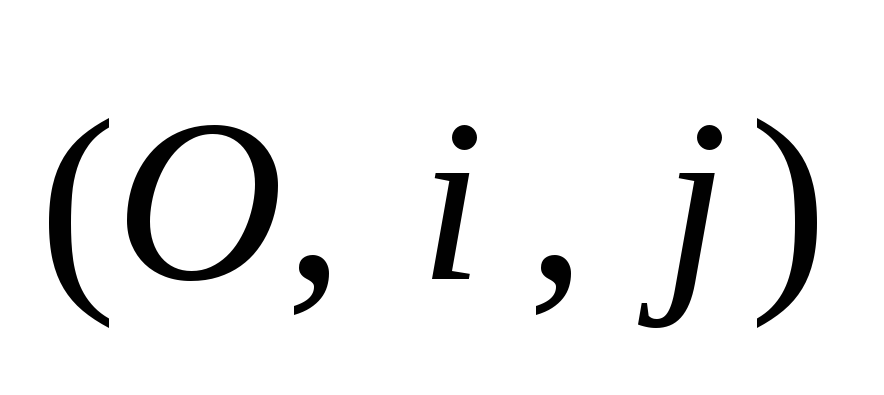, если в этом репере заданы координаты фокуса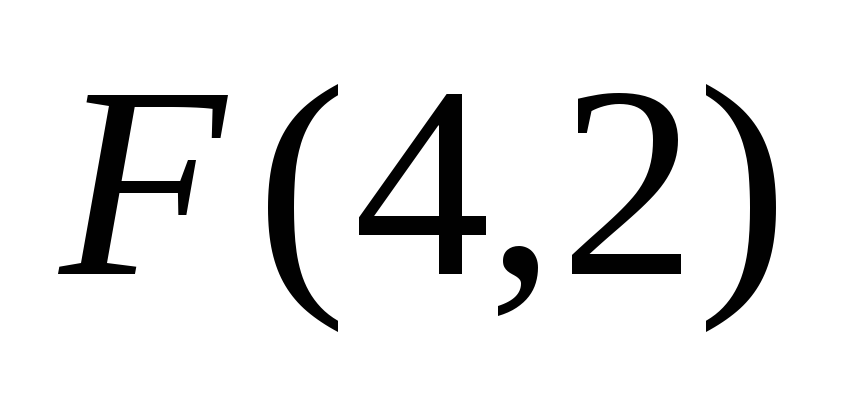и уравнение директрисы: х+3у+6=0. Определить параметр параболы.

2. На прямой, уравнение которой в репере 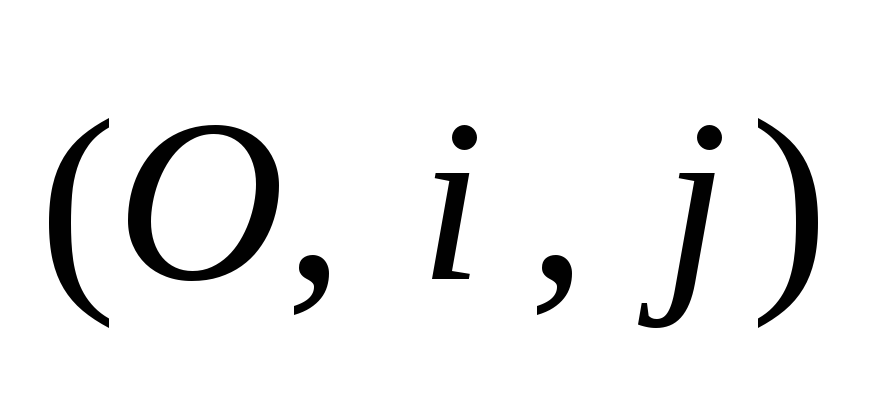8х–3у+6=0, найти точку, которая одинаково удалена от прямой:х–5=0 и точкиА(–3, 2).

3. Высота параболической арки равна h, а ширина ее основания равна. Найти параметр параболы.

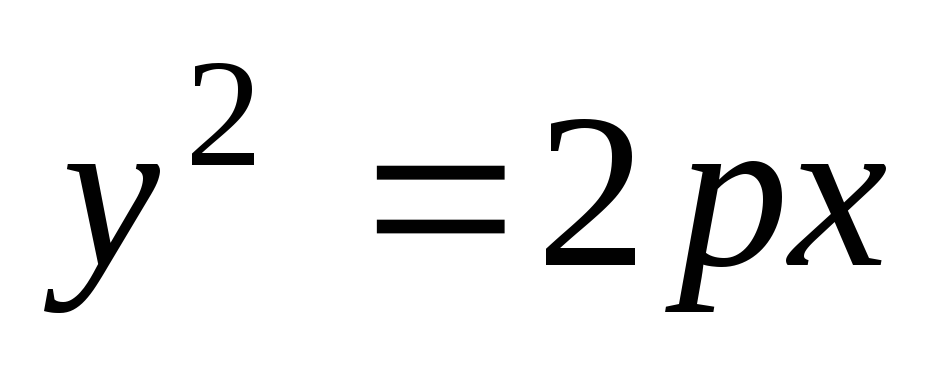4. Прямая х–3у+9=0 касается параболы. Найтиp.

5. Найти расстояние между параболой и прямой 4х+3у+46=0.

6. Найти фигуру, образованную основаниями перпендикуляров, опущенных из фокуса параболы на касательные к этой параболе.

7. Доказать, что фокус параболы и точки касания двух касательных к параболе, проведенных из любой точки директрисы, лежат на одной прямой.

8. Доказать оптическое свойство параболы: всякая касательная к параболе составляет равные углы с фокальным радиусом точки и с лучом, проходящим через точку касания и сонаправленным с ее осью.

9. Найти множество центров всех окружностей, походящих через данную точку Аи касающихся данной прямойl.

10. На чертеже изображена парабола. Пользуясь циркулем и линейкой, построить прямую, параллельную ее главному диаметру.

Задачи повышенной трудности

1. Доказать, что произведение длин отрезков перпендикуляров, проведенных из концов любой хорды на ось параболы, проходящей через ее фокус, постоянно.

2. Найти множество середин всех хорд параболы, проходящих через ее фокус.

3. Найти сторону правильного треугольника, вписанного в параболу, заданную уравнением .

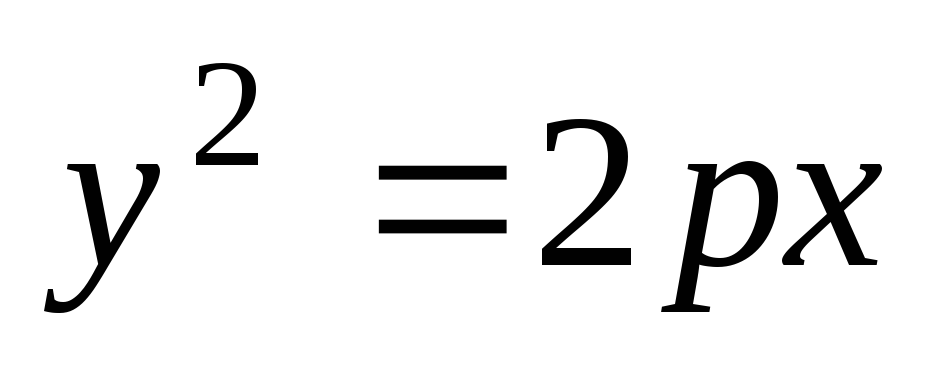Домашнее задание

1. Камень, брошенный под острым углом к горизонту, описал дугу параболы и упал на расстоянии 16 м от начального положения. Определить фокальный параметр параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12 м.

2. Написать каноническое уравнение параболы, которая задана в полярной системе координат уравнением .

3. Написать уравнение параболы, если известен ее параметр , фокуси уравнение директрисы.

Тема 3.5. Пересечение линии второго порядка с прямой. Асимптотические направления и асимптоты

Литература: [1], гл. 17, § 3, стр. 434–440; [7], гл. 4, § 32, стр. 109–114.

Основные сведения

Направление, определяемое ненулевым вектором , является асимптотическим направлением относительно линии второго порядка, заданной общим уравнением, тогда и только тогда, когда.

Если то, где,.

Если , то асимптотические направления определяются векторамии.

Теорема. Если>0, то линия второго порядка не имеет асимптотических направлений, если=0, то – одно асимптотическое направление, если<0, то – два асимптотических направления.

Лемма. Направление ненулевого вектораявляется асимптотическим направлением относительно линии второго порядка параболического типа, заданного общим уравнением, тогда и только тогда, когда.

Вопросы для повторения

1. Как могут располагаться на плоскости кривая второго порядка и прямая?

2. Какое направление называется асимптотическим относительно линии второго порядка?

3. Сколько различных асимптотических направлений может иметь линия второго порядка?

4. Приведите примеры линий, которые: 1) не имеют асимптотических направлений; 2) имеют одно асимптотическое направление; 3) имеют два асимптотических направления; 4) имеют более двух асимптотических направлений.

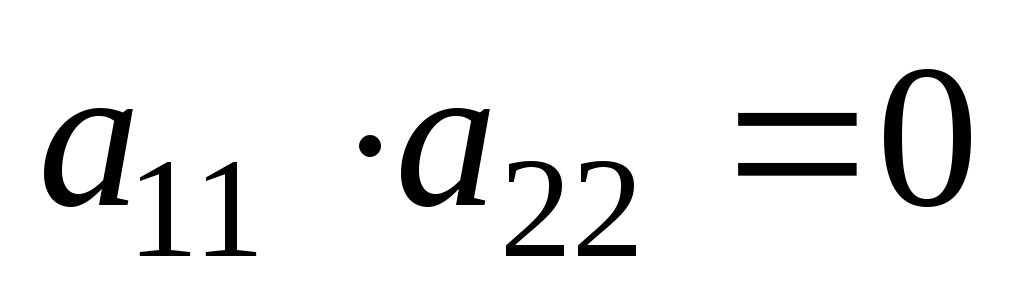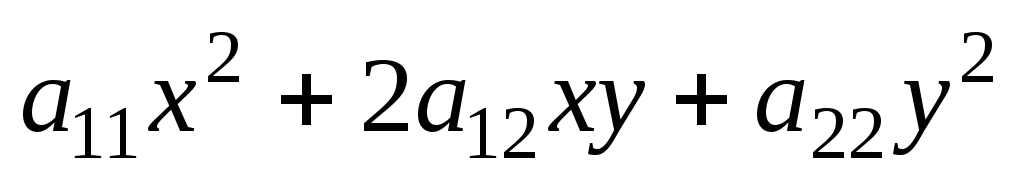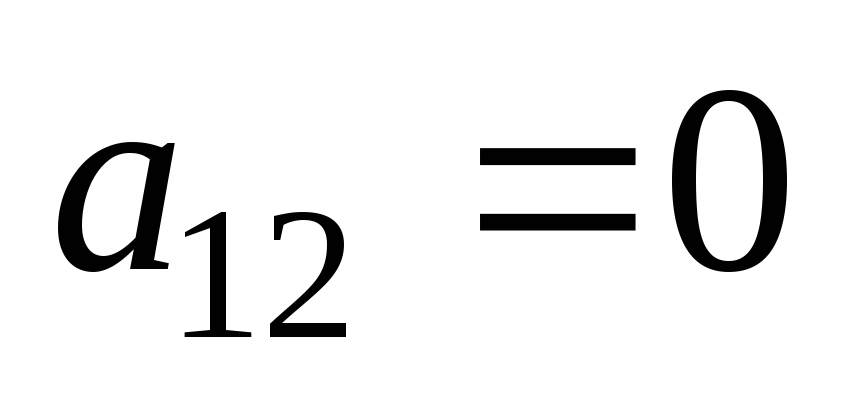
5. Может ли иметь асимптотические направления линия второго порядка, если: а) для коэффициентов общего уравнения линии второго порядка выполнено условие ; б) члены второго порядкаиз ее общего уравнения образуют полный квадрат; в)и.

Задачи

1. Выяснить, имеют ли оси координат асимптотическое направление относительно линии второго порядка, заданного уравнением:

а)

б)

в)

г) ?

2. Найти векторы асимптотического направлений линии второго порядка, заданной уравнением:

а) ;

б) ;

в) .

3. Через точку A(2,0) проведены две прямые, имеющие лишь по одной общей точке с линией, заданной в прямоугольной декартовой системе координат уравнением. Написать уравнения этих прямых и найти угол между ними.

4. Написать общее уравнение линии второго порядка, для которой ось абсцисс: а) имеет асимптотическое направление; б) не имеет с линией общих точек.

5. Написать уравнение гиперболы, проходящей через точку A(0,5) и имеющей асимптоты, заданные уравнениями.

6. Написать уравнение кривой второго порядка, для которой оси координат являются асимптотами и которая: 1) проходит через начало координат; 2) проходит через точку (1, 2).

Задачи повышенной трудности

1. Какой вид имеет общее уравнение линии второго порядка, имеющего пересекающиеся прямые своими асимптотами.

2. Какому условию удовлетворяют коэффициенты общего уравнения гиперболы, заданного в прямоугольной декартовой системе координат, если гипербола равносторонняя?

3. Пусть кривая второго порядка дана общим уравнением , коэффициенты которого удовлетворяют условиям, где . Доказать, что если координаты вектора удовлетворяют условиям , то прямая, параллельная вектору, является асимптотой кривой.

4. Доказать, что две линии второго порядка, заданные общими уравнениями, имеют общие асимптоты тогда и только тогда, когда все соответствующие коэффициенты их уравнений, кроме свободных членов, пропорциональны.

Домашнее задание

1. Написать общее уравнение линии второго порядка, для которой обе координатные оси: а) имеют асимптотические направления; б) не имеют с линией общих точек.

2. Написать уравнения прямых, проходящих через начало координат и пересекающих линию, заданную уравнением

,

лишь в одной точке.

3. Написать уравнения асимптот следующих кривых:

1) ; 2).