
- •Министерство образования и науки
- •Введение
- •Раздел 1. Элементы векторной алгебры в пространстве.
- •Тема 1.1. Направленные отрезки. Векторы.
- •Тема 1.2. Умножение векторов на действительные числа
- •Тема 1.3. Коллинеарные и компланарные векторы.
- •Тема 1.4. Скалярное произведение векторов
- •Тема 1.5. Векторные подпространства
- •Тема 1.6. Применение векторов к решению задач
- •Задачи повышенной трудности
- •Домашнее задание
- •Индивидуальные задания по векторной алгебре Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Раздел 2. Метод координат на плоскости
- •Тема 2.1. Аффинная система координат. Аффинные задачи
- •Задачи повышенной трудности
- •Тема 2.2. Прямоугольная система координат. Аффинные и метрические задачи
- •Тема 2.3. Полярная система координат. Метрические задачи
- •Тема 2.4. Ориентация плоскости. Преобразования координат на плоскости
- •Тема 2.5. Геометрическое истолкование уравнений и неравенств между координатами. Алгебраические линии.
- •Домашнее задание
- •Тема 2.6. Уравнения прямой в аффинной и прямоугольной декартовой системах координат. Аналитическое задание полуплоскости
- •Тема 2.7. Взаимное расположение двух прямых.
- •Тема 2.8. Расстояние от точки до прямой. Угол между двумя прямыми
- •Задачи повышенной трудности
- •Тема 2.9. Аффинные и метрические задачи на прямую. Решение задач школьного курса методом координат
- •Раздел 3. Кривые второго порядка
- •Тема 3.I. Окружность
- •Задачи повышенной трудности
- •Домашнее задание
- •Тема 3.2. Эллипс
- •Задачи повышенной трудности
- •Тема 3.3. Гипербола
- •Задачи повышенной трудности
- •Тема 3.4.Парабола
- •Задачи повышенной трудности
- •Тема 3.5. Пересечение линии второго порядка с прямой. Асимптотические направления и асимптоты
- •Тема 3.6. Центр линии второго порядка. Касательная
- •Тема 3.7. Сопряженные направления. Главные направления. Диаметры линии второго порядка
- •1) Эллипса ; 2) гиперболы.
- •Тема 3.8. Приведение общего уравнения кривой второго порядка к каноническому виду
- •Индивидуальные задания по кривым второго порядка
Тема 2.8. Расстояние от точки до прямой. Угол между двумя прямыми
Литература: [1], гл. 5,§ 8–9, стр. 107–112; [7], гл. 3, § 23, 24, стр. 80–85.
Основные определения, теоремы и формулы
В прямоугольной
системе координат расстояние от точки
![]() до прямой
до прямой![]() ,
заданной уравнением
,
заданной уравнением![]() вычисляется по формуле:
вычисляется по формуле:![]() .
.
Пусть даны две прямые
![]() и
и![]() .
Выберем направляющие векторы
.
Выберем направляющие векторы![]() и
и![]() этих
прямых так, чтобы направленный угол
между ними был не больше прямого угла.
Тогда направленный угол
этих
прямых так, чтобы направленный угол
между ними был не больше прямого угла.
Тогда направленный угол![]() между
векторами
между
векторами![]() и
и![]() называетсянаправленным углом между
прямыми
называетсянаправленным углом между
прямыми![]() и
и![]() :
: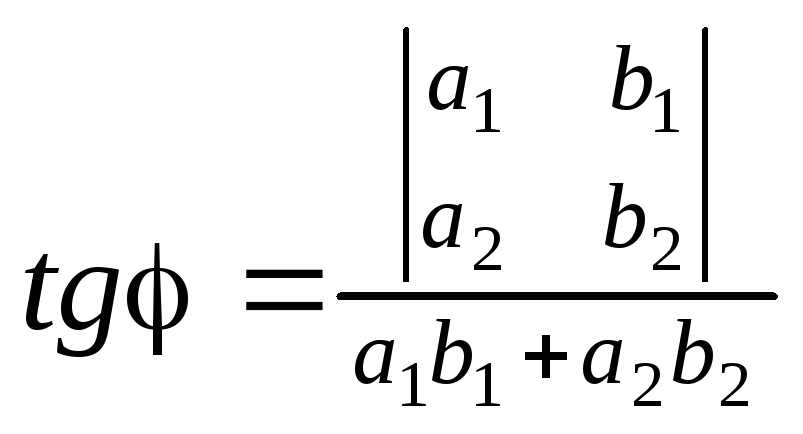 ,
где
,
где![]() и
и![]() соответственно координаты векторов
соответственно координаты векторов![]() и
и![]() в ортонормированном базисе.
в ортонормированном базисе.
Вопросы для самоконтроля
Что такое «расстояние от точки до прямой»?
Как определяется расстояние от точки до фигуры?
Вывести формулу для вычисления расстояния от точки M(x0,y0) до прямойAx+By+C=0.
Сформулировать определение угла между прямыми и пояснить на примере.
Вывести формулу для вычисления угла между двумя прямыми.
Какой вид примет формула для вычисления угла между прямыми, если прямые заданы: а) общими уравнениями
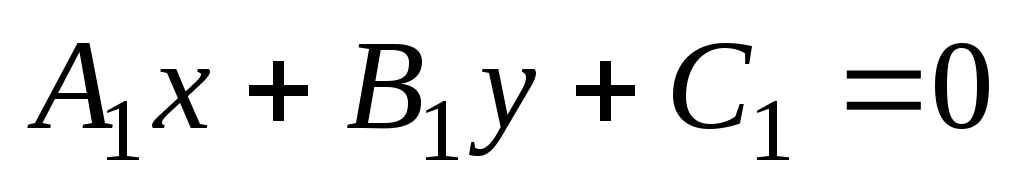 и
и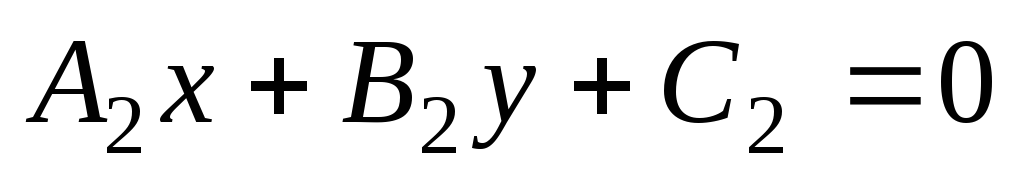 ;
б) уравнениями с угловыми коэффициентами
;
б) уравнениями с угловыми коэффициентами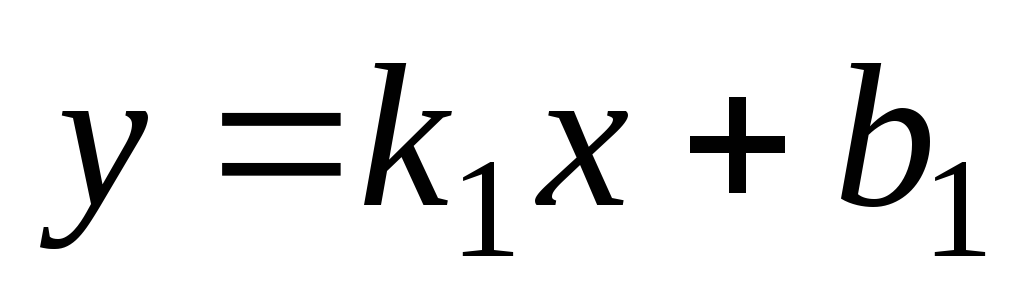 и
и ?
?Запишите условие перпендикулярности двух прямых в каждом из случаев, указанных выше.
Задачи
1. Написать уравнение прямой, проходящей через точку A(–1,4), если расстояние от этой прямой до точкиB(–2, –1) равно 5.
2. Найти координаты центра окружности, вписанной в треугольник ABC, если: а)A(2,1),B(–1,4),C(3, –1); б)A(0,1),B(–1,2),С(2,3).
3. Написать уравнения прямых, отстоящих от прямой, заданной уравнением 4x–3y–7=0, на расстоянии, равном 4.
Написать уравнения прямых, симметрия относительно которых переводит прямую x+y+1=0 в прямую 2x–y=0.
Начало координат является центром квадрата, уравнение одной из прямых, содержащих сторону квадрата, имеет вид x+2y–1=0. Вычислить координаты вершин квадрата.
Точка M(3, –2) принадлежит основаниюBCравнобедренного треугольникаABC. Написать уравнение прямойBC, если
AC: 4x–3y+7=0, AB: 3x–4y–3=0.
Написать уравнение прямой, содержащей биссектрису того из углов между прямыми, заданными уравнениями x+2y–5=0 и 3x–6y+2=0, внутри которого лежит начало координат.
8. Луч света, направленный по прямой, заданной уравнением x+y+3=0, отражается от прямой, заданной уравнением 3x-y+5=0. Написать уравнение прямой, на которой лежит отраженный луч.
Задачи повышенной трудности
1. Найти вершины квадрата ABCD, диагональACкоторого лежит на прямойx-y+1=0, вершинаB– на прямойx–4=0, вершинаD– на окружности, заданной уравнениемx2+y2–2x–10y+22=0.
2. Найти множество
всех точек плоскости, отношение расстояний
от каждой из которых до двух заданных
прямых равно отношению данных отрезков
![]() и
и![]() ,
если данные прямые: а) параллельны; б)
пересекаются.
,
если данные прямые: а) параллельны; б)
пересекаются.
3. В треугольник ABC с вершинами A(–1,0), B(7,0), C(1,4) вписан прямоугольник PQMN так, что точки P и Q лежат на стороне AB, а точки M и N – соответственно на сторонах BC и AC. Составить уравнения сторон прямоугольника PQMN, если известно, что PQ = 2QM.
Домашнее задание
1. На оси абсцисс найти точку, равноудаленную от прямых, которые заданы уравнениями x+3y+2=0 и 3x-y+1=0.
2. Составить уравнения прямых, содержащих катеты равнобедренного прямоугольного треугольника ABC, зная координаты вершиныC(4, –1) прямого угла и уравнение прямой 3x–y+5=0, содержащей гипотенузуABэтого треугольника.
3. Доказать, что прямые, заданные уравнениями
7x–5y+11=0, 3x+2y–16=0, 4x–7y–2=0,
образуют треугольник, и вычислить тангенсы внутренних углов этого треугольника.
