
- •Министерство образования и науки
- •Введение
- •Раздел 1. Элементы векторной алгебры в пространстве.
- •Тема 1.1. Направленные отрезки. Векторы.
- •Тема 1.2. Умножение векторов на действительные числа
- •Тема 1.3. Коллинеарные и компланарные векторы.
- •Тема 1.4. Скалярное произведение векторов
- •Тема 1.5. Векторные подпространства
- •Тема 1.6. Применение векторов к решению задач
- •Задачи повышенной трудности
- •Домашнее задание
- •Индивидуальные задания по векторной алгебре Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Раздел 2. Метод координат на плоскости
- •Тема 2.1. Аффинная система координат. Аффинные задачи
- •Задачи повышенной трудности
- •Тема 2.2. Прямоугольная система координат. Аффинные и метрические задачи
- •Тема 2.3. Полярная система координат. Метрические задачи
- •Тема 2.4. Ориентация плоскости. Преобразования координат на плоскости
- •Тема 2.5. Геометрическое истолкование уравнений и неравенств между координатами. Алгебраические линии.
- •Домашнее задание
- •Тема 2.6. Уравнения прямой в аффинной и прямоугольной декартовой системах координат. Аналитическое задание полуплоскости
- •Тема 2.7. Взаимное расположение двух прямых.
- •Тема 2.8. Расстояние от точки до прямой. Угол между двумя прямыми
- •Задачи повышенной трудности
- •Тема 2.9. Аффинные и метрические задачи на прямую. Решение задач школьного курса методом координат
- •Раздел 3. Кривые второго порядка
- •Тема 3.I. Окружность
- •Задачи повышенной трудности
- •Домашнее задание
- •Тема 3.2. Эллипс
- •Задачи повышенной трудности
- •Тема 3.3. Гипербола
- •Задачи повышенной трудности
- •Тема 3.4.Парабола
- •Задачи повышенной трудности
- •Тема 3.5. Пересечение линии второго порядка с прямой. Асимптотические направления и асимптоты
- •Тема 3.6. Центр линии второго порядка. Касательная
- •Тема 3.7. Сопряженные направления. Главные направления. Диаметры линии второго порядка
- •1) Эллипса ; 2) гиперболы.
- •Тема 3.8. Приведение общего уравнения кривой второго порядка к каноническому виду
- •Индивидуальные задания по кривым второго порядка
Тема 2.9. Аффинные и метрические задачи на прямую. Решение задач школьного курса методом координат
Литература: [1], гл. 5, § 1-10, стр. 87–114; [7], гл.2, § 19, стр. 68–72, гл. 3, §25, стр. 85–88.
Задание на плоскости системы координат позволяет определить точки плоскости с помощью пар чисел, а любую фигуру, как множество точек, можно тогда определить с помощью уравнений, неравенств или их систем и тем самым при доказательстве теорем или решении геометрических задач можно использовать аналитические методы.
В этом и заключается суть метода координат на плоскости.
Использование метода координат позволяет алгоритмизировать процесс решения геометрических задач.
Этот алгоритм содержит следующие этапы:
Выделим условие (данные) и заключение (требуемое) в задаче. Определим, какая это задача – аффинная или метрическая. При необходимости построим чертеж.
Если задача аффинная, то выберем на плоскости удобную аффинную систему координат. Если же задача метрическая, то выберем либо прямоугольную, либо полярную систему координат.
Переведем данные и требуемое в задаче на язык координат.
С помощью выкладок (вычислений) получим из данных требуемое.
Рассмотрим применение этого алгоритма при решении конкретной задачи.
Пример.Дан
треугольникАВСи точки![]() ,
,![]() ,
,![]() ,
отличные от вершин. Доказать, что прямые(АА1), (ВВ1), (СС1)
пересекаются в одной точке тогда и
только тогда, когда
,
отличные от вершин. Доказать, что прямые(АА1), (ВВ1), (СС1)
пересекаются в одной точке тогда и
только тогда, когда![]() (теорема
Чевы).
(теорема
Чевы).
Замечаем, что здесь представлены две взаимообратные задачи.
Задача 1.Дан
треугольникАВСи точки![]() ,
,![]() ,
,![]() .
Если
.
Если![]() ,
то (АА1),(ВВ1), (СС1)
пересекаются в одной точке (Рис. 24)
,
то (АА1),(ВВ1), (СС1)
пересекаются в одной точке (Рис. 24)
З адача2.Дан треугольникАВСи точки
адача2.Дан треугольникАВСи точки![]() ,
,![]() ,
,![]() .
Если прямые (АА1), (ВВ1),
(СС1) пересекаются в одной
точке, то
.
Если прямые (АА1), (ВВ1),
(СС1) пересекаются в одной
точке, то![]() .
.
Решим задачу 1.
Дано:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Доказать: ![]() .
.
Решение:Так как
в задаче говорится только о делении
отрезков в заданных отношениях и
пересечениях прямых, то это аффинная
задача и для ее решения можно выбрать
аффинную систему координат. Выберем
аффинный репер![]() .
ТогдаА(0, 0),В(0, 1),С(1, 0),С1(0,
у),В1(х,0),А1(х1,
у1). Обозначим
.
ТогдаА(0, 0),В(0, 1),С(1, 0),С1(0,
у),В1(х,0),А1(х1,
у1). Обозначим![]() ,
,![]() .
Тогда по условию задачи
.
Тогда по условию задачи![]() .
Определим координаты точекА1,В1,С1по известной
формуле деления отрезка в заданном
отношении:
.
Определим координаты точекА1,В1,С1по известной
формуле деления отрезка в заданном
отношении:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Значит,
![]() ,
,![]() ,
,![]() .
.
Составим уравнение прямых (АА1), (ВВ1), (СС1). Замечаем, что при составлении уравнения прямых (ВВ1) и (СС1) можно воспользоваться уравнением прямых в отрезках.
(ВВ1):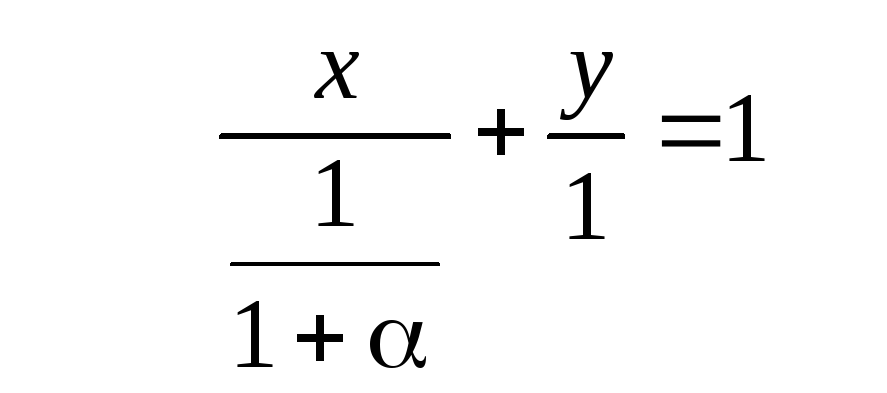 или
или![]() .
.
(СС1):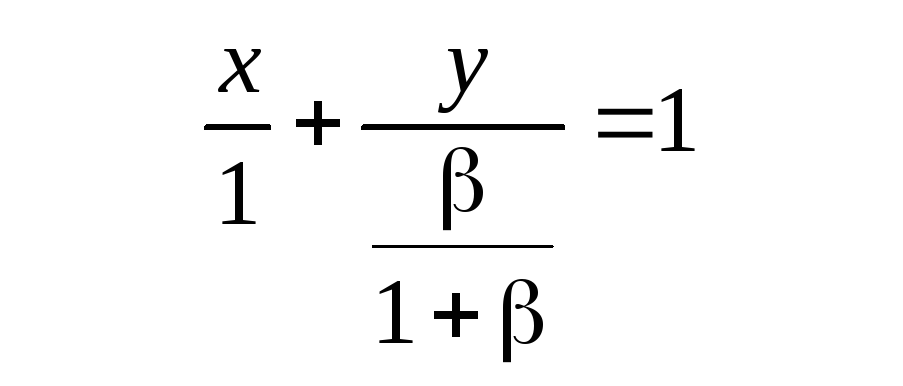 или
или![]() .
.
(АА1):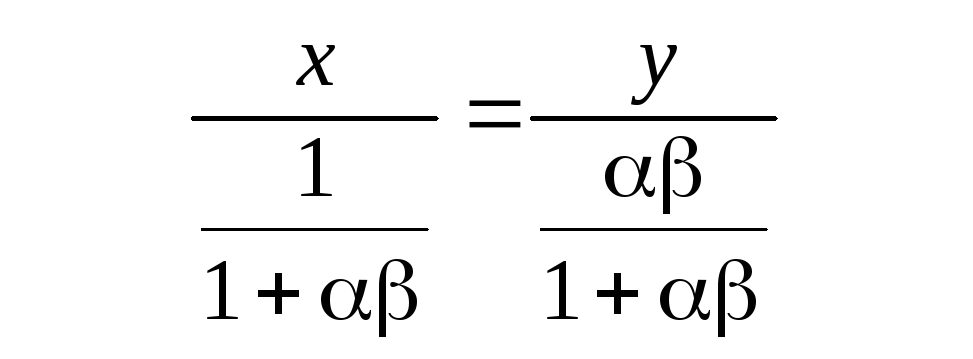 или
или![]() .
.
Определим координаты
точки
![]() :
:
![]()
Отсюда
![]() ;
;
![]() ;
;![]() .
.
Подставив координаты
точки Мв уравнение прямой (СС1),
получим тождество:![]() .
Следовательно,
.
Следовательно,![]() .
.
Задача 2 так же
решается методом координат. Выберем
аффинный репер
![]() .
ТогдаА(0,
0), В(0,
1), С(1,
0). Обозначим
.
ТогдаА(0,
0), В(0,
1), С(1,
0). Обозначим
![]() ,
,![]() и последовательно выполним следующие
действия: 1) вычислим координаты точек
и последовательно выполним следующие
действия: 1) вычислим координаты точек![]() и
и![]() ;
2) составим уравнения прямых
;
2) составим уравнения прямых![]() и
и![]() ;
3) определим координаты точки
;
3) определим координаты точки![]() ;
4) составим уравнение прямой
;
4) составим уравнение прямой![]() ;
5) определим координаты точки
;
5) определим координаты точки![]() – точки пересечения прямых
– точки пересечения прямых![]() и
и![]() ;
6) вычислим
;
6) вычислим![]() и убедимся, что оно равно
и убедимся, что оно равно![]() .
.
С интересными примерами применения метода координат можно познакомиться в [1, §§ 19, 26].
Задачи
1. Методом координат доказать, что в любом треугольнике пересекаются в одной точке: 1) медианы; 2) высоты; 3) биссектрисы.
2. Доказать, что сумма
квадратов расстояний от всех вершин
квадрата до прямой, проходящей через
его центр, не зависит от выбора прямой.
Найти эту сумму, если сторона квадрата
равна
![]() .
.
3. Найти множество центров тяжести всех треугольников, две вершины которых зафиксированы, а третьи вершины лежат на данной прямой.
4. В плоскости треугольника ABCдана произвольная точкаM. ТочкиM1,M2,M3симметричны точкеMотносительно середин сторонBC,CA,AB соответственно. Доказать, что прямыеAM1,BM2,CM3пересекаются в одной точке.
5. Точки EиM– середины сторонADиBCпараллелограммаABCD. Доказать, что прямыеBEиMDделят диагональACпараллелограмма на три равные части.
6. Даны две параллельные
прямые
![]() и
и![]() .
Найти множество точек, делящих в одном
и том же отношении
.
Найти множество точек, делящих в одном
и том же отношении![]() все
отрезкиLD, концы которых соответственно
лежат на прямых
все
отрезкиLD, концы которых соответственно
лежат на прямых![]() и
и![]() .
.
7. Доказать, что сумма квадратов расстояний от фиксированной точки, взятой в плоскости данной окружности, до концов произвольного диаметра этой окружности есть величина постоянная, не зависящая от выбора диаметра.
Задачи повышенной трудности
Доказать, что произведение любых двух сторон треугольника равно произведению его высоты, проведенной из их общей вершины, на диаметр описанной окружности.
Доказать, что каждая прямая, проходящая через основания высот, проведенных из двух вершин непрямоугольного треугольника, перпендикулярна прямой, проходящей через его третью вершину и центр окружности, описанной около этого треугольника.
Найти множество точек пересечения диагоналей прямоугольников, вписанных в данный треугольник так, что две соседние вершины каждого прямоугольника лежат на основании треугольника, а две другие на боковых сторонах.
Домашнее задание
В квадрат вписана окружность. Доказать, что сумма квадратов расстояний от любой точки окружности до сторон квадрата не зависит от выбора точки на окружности. Найти эту сумму, если сторона квадрата равна 2
 .
.Найти множество точек плоскости, сумма квадратов расстояний, от каждой из которых до концов одной диагонали прямоугольника равна сумме квадратов расстояний до концов другой его диагонали.
Даны две параллельные прямые
 и
и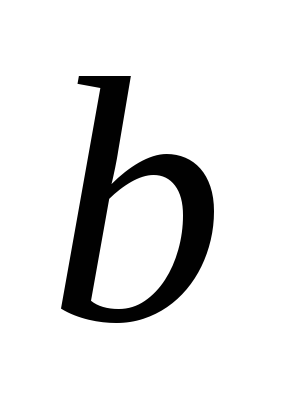 ,
и их центр симметрииM.
Через точкуMпроведены
две произвольные, взаимно перпендикулярные
прямыеsиl,
пересекающие прямые
,
и их центр симметрииM.
Через точкуMпроведены
две произвольные, взаимно перпендикулярные
прямыеsиl,
пересекающие прямые и
и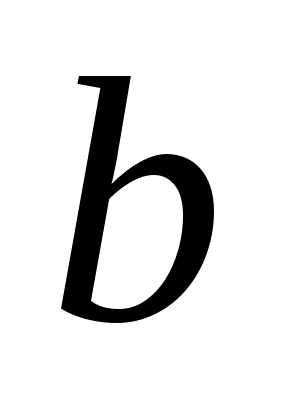 соответственно в точкаAиB.
Доказать, что расстояние от точкиMдо прямойABне зависит от выбора
прямыхsиl.
соответственно в точкаAиB.
Доказать, что расстояние от точкиMдо прямойABне зависит от выбора
прямыхsиl.
Индивидуальные задания
Вариант 1
Точки A(1,1),B(–1,2),C(2,–1) – три вершины равнобочной трапеции. Вычислить координаты четвертой вершины.
Фигура Fзадана уравнением
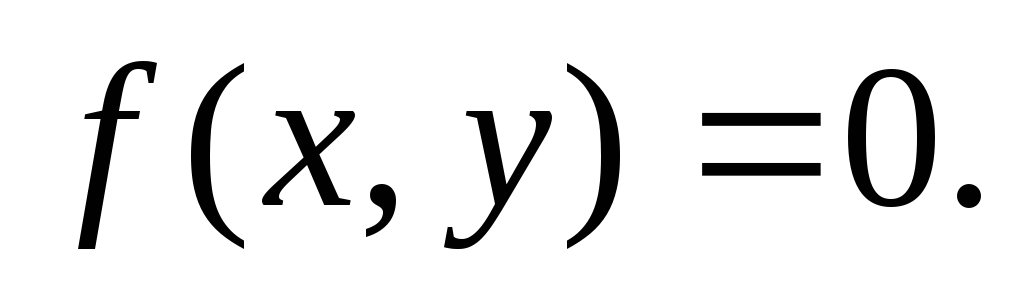 Какую фигуру задает уравнение: 1)
Какую фигуру задает уравнение: 1)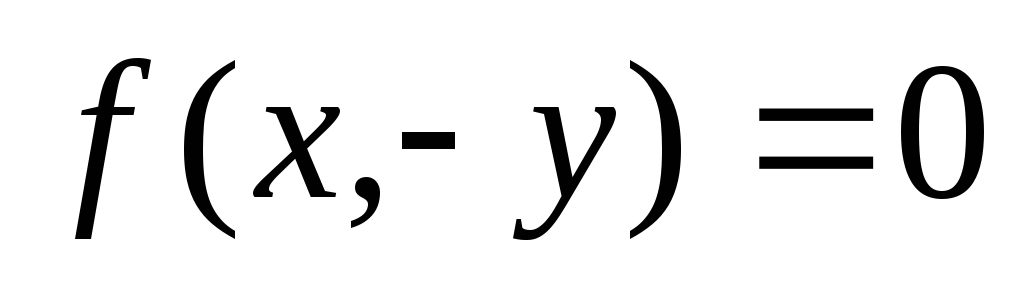 ;
2)
;
2)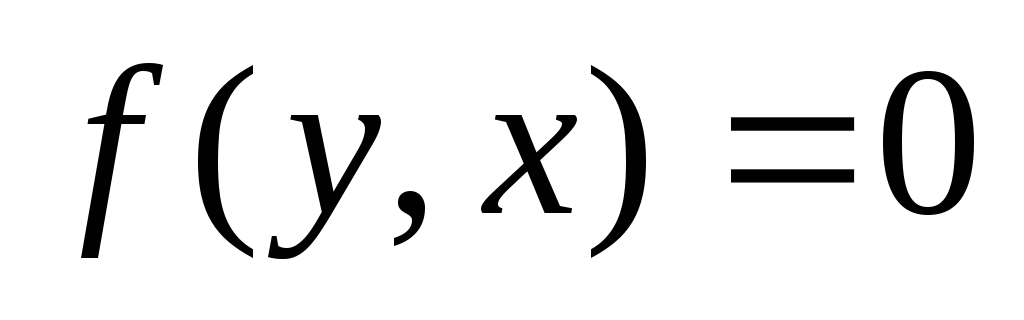 ;
3)
;
3)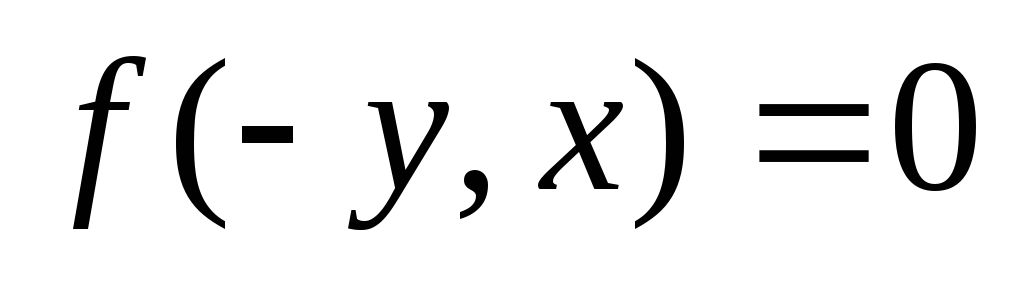 .
.Составить уравнение множества центров тяжести треугольников, имеющих две вершины A(x1,y1),B(x2,y2), если третья вершина лежит на окружности радиуса
 ,
центр которой – начало координат.
,
центр которой – начало координат.На прямой 2x–y–10=0 найти точку, сумма расстояний от которой до точекA(–5,0) иB(–3,4) была бы наименьшей.
Какие координаты будет иметь точка Aв аффинной системе координат (
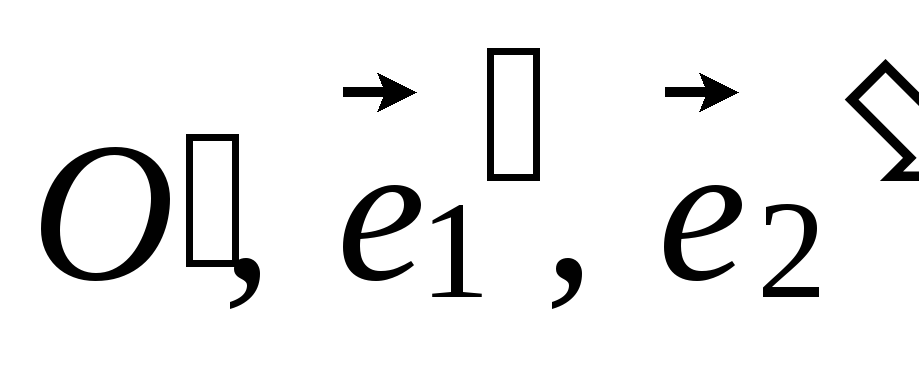 ),
если в репере (O,
),
если в репере (O, ):A(3,–1),
):A(3,–1),
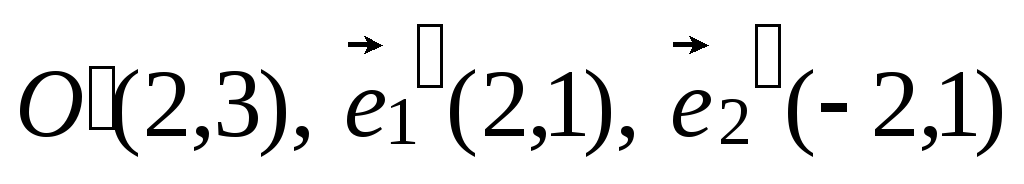 .
.
Вариант 2
Две прямые x+y–2=0,x+y+3=0 повернуты вокруг начала координат на 900. Найти координаты точек пересечения данных прямых и их образов при повороте. Доказать, что полученные точки являются вершинами квадрата.
Отрезок постоянной длины движется так, что один его конец скользит по окружности x2+y2 =r2, а другой – по осиOx (шатунно-кривошипный механизм). Составить уравнение кривой, которую описывает точка отрезка, разделяющая его на части
 и
и
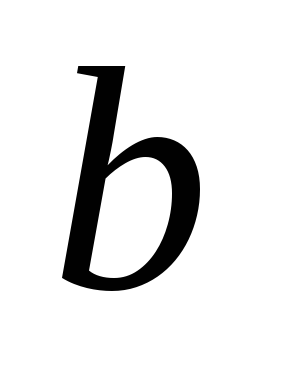 .
.Прямая dпроходит через вершинуAи середину медианыBMтреугольникаABC,N– точка пересечения прямойdсо сторонойBC. Доказать, что отношение (BC,N)=
 .
.В системе координат (O,
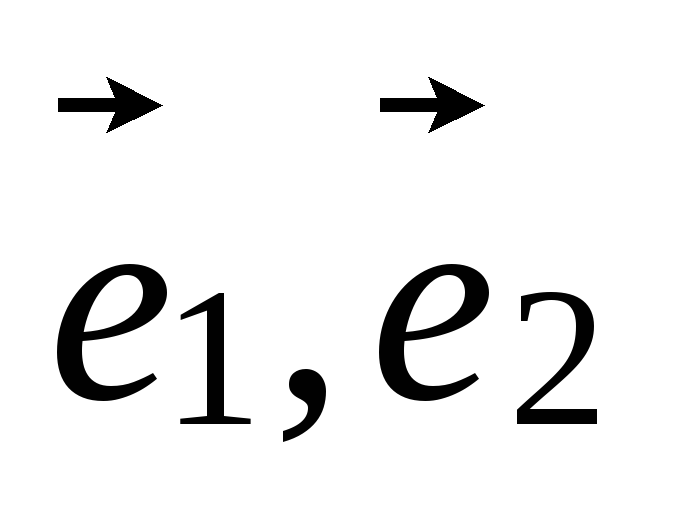 )
даны линии уравнениями:
)
даны линии уравнениями:
1) x–2y+1=0; 2)x+y=0; 3)y–3=0. Найти уравнения
тех же линий в системе (![]() ),
если
),
если![]() .
.
Вычислить площадь параллелограмма ABCDпо координатам трех его вершин в репере (O,
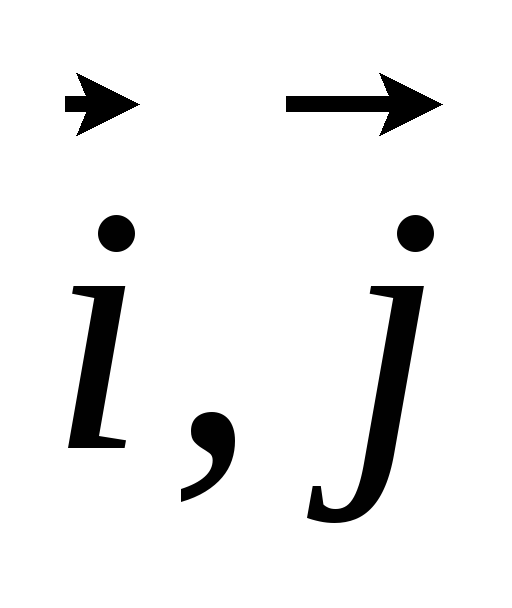 ):
1)A(3,1),B(–1,0),C(2,–1); 2)A(3,–1),B(2,1),C(–3,0).
):
1)A(3,1),B(–1,0),C(2,–1); 2)A(3,–1),B(2,1),C(–3,0).
Вариант 2
Дан треугольник ABC. Прямаяdпересекает прямыеBC,CA,ABсоответственно в точкахA1,B1иC1. На каждой прямой построены точкиA2,B2,C2симметричные точкамA1,B1,C1относительно середины содержащих их сторон. Доказать, что точкиA2,B2иC2принадлежат на одной прямой.
Найти множество точек плоскости, для каждой из которых расстояние до данной точки A вдвое больше расстояния до данной прямойa, проходящей через точкуA.
Написать аналитические условия, определяющие треугольник ABC, если: 1)A(3,1),B(–2,0),C(0,1); 2)A(–3,1),B(2,0),C(0,1).
На сторонах прямого угла ACBданы две точкиAиBтак, чтоCA=CB. Найти множество точекM, расположенных внутри угла, для которых лучMCесть биссектриса углаAMB.
Написать формулы преобразования прямоугольных декартовых координат в каждом из следующих случаев:
1)
![]() и системы координат (
и системы координат (![]() )
и (
)
и (![]()
![]() )
ориентированы одинаково; 2)
)
ориентированы одинаково; 2)![]() (
(![]() )=300и системы координат (
)=300и системы координат (![]() )
и (
)
и (![]()
![]() )
ориентированы противоположно.
)
ориентированы противоположно.
Вариант 3
По координатам концов двух отрезков AB иCDвыяснить, имеют ли они общую точку: 1)A(3,1),B(–2,0),C(0,1),D(–3,2); 2)A(1,0),B(2,4),C(3,0),D(0,6).
Через точку Mк сторонам треугольника проведены перпендикуляры. Найти множество точекM, для каждой из которых основания перпендикуляров принадлежат одной прямой.
На луче x=2+3t,y=1–2t,t ≤ 0 найти точкуB, расстояние от которой до начала луча равно 5.
Написать аналитические условия, определяющие параллелограмм ABCD, если: 1)A(0,1),B(–1,2),C(1,3); 2)A(1,1),B(–2,0),C(3,–1).
Найти координаты точки, имеющей одни и те же координаты в системах (O,
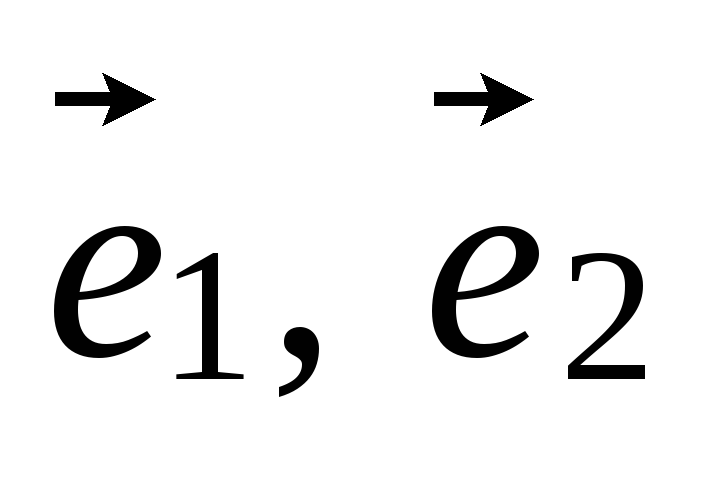 )
и (
)
и (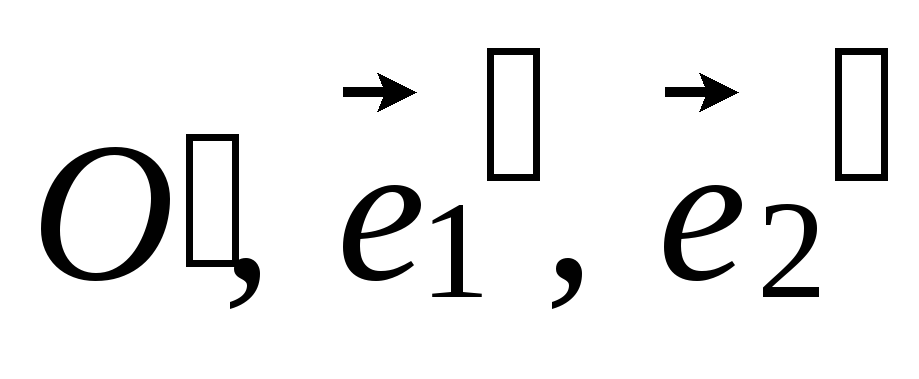 ),
где
),
где
 .
.Доказать, что треугольник ABC– равнобедренный, и составить уравнение его оси симметрии: 1)A(2,1),B(4,3),C(2,3).
Вариант 4
На луче x=2+3t,y=1–2t,t ≤ 0 найти точкуB, расстояние от которой до начала луча равно 3.
Дана прямая d и точкаA. Вычислить координаты основания перпендикуляра, проведенного из точкиAна прямуюd, если:
1) d: 3x+4y–1=0, A(2,–1); 2) d: x+3y+2=0, A(–2,3).
Даны уравнения прямых, содержащих высоты треугольника, и координаты одной из вершин треугольника. Вычислить координаты двух других вершин этого треугольника:
1) 3x+4y–7=0, 2x–y–1=0, A(5,–3); 2) 3x+4y–2=0, 4x–y+2=0, A(0,–1).
В равнобедренном треугольнике ABC(AB=BC) даны координаты вершинA(4,3),B(–1,2) и уравнение прямойBD: 3x–2y+7=0, перпендикулярнойAC. Написать уравнения прямыхABиBC.
Через точку пересечения медиан треугольника проведена прямая d. Найти соотношение между расстояниями от вершин треугольника до прямойd.
Вариант 5
Написать аналитические условия, определяющие параллелограмм ABCD, если: 1)A(0,1),B(–1,2),C(1,3); 2)A(1,1),B(–2,0),C(3,–1).
Вычислить координаты орта нормали прямой:
1) x+2y–3=0; 2)x=2t–1,y=5t+4;
3)
![]() .
.
Найти координаты точки, имеющей одни и те же координаты в системах (O,
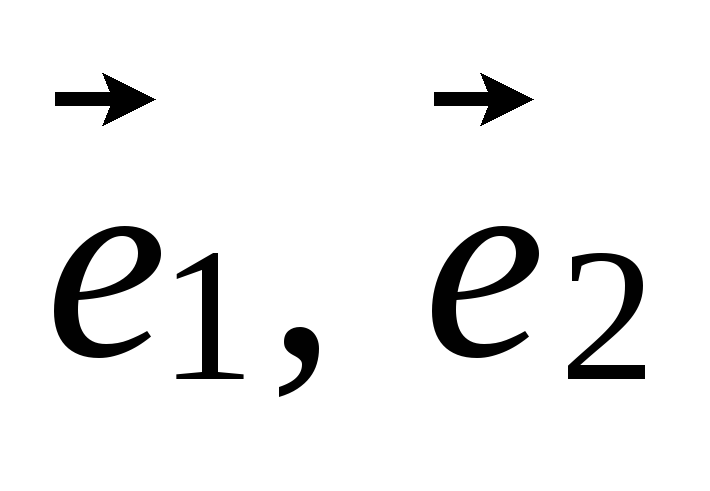 )
и (
)
и (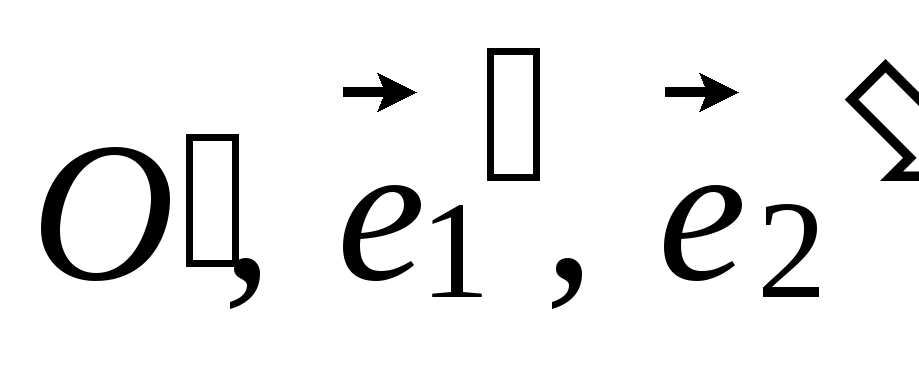 ),
где
),
где
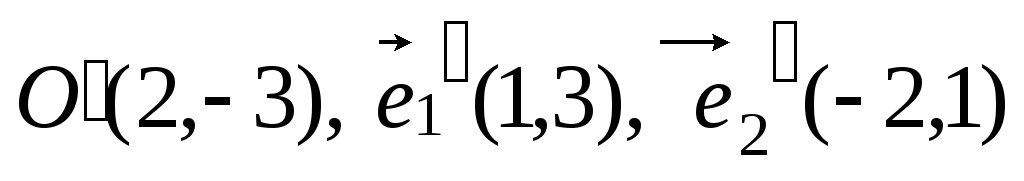 .
.Даны точки A(5,2) иB(2,1). На прямойx+y–5=0 найти точкуM, такую, чтобы
 AMB=450.
AMB=450.Точки M иN принадлежат соответственно сторонамDCиCBпараллелограммаABCD. Через середину отрезковDMиABпроведена прямая. Через середину отрезковADиBN– вторая прямая, пересекающая первую в точкеP. Доказать, что прямаяAPпроходит через середину отрезкаMN.
Вариант 6
Прямоугольную декартову систему координат (
 )
повернули вокруг начала координат на
угол +450. Найти уравнения: 1) новых
координатных осей в старой системе; 2)
старых координатных осей в новой
системе.
)
повернули вокруг начала координат на
угол +450. Найти уравнения: 1) новых
координатных осей в старой системе; 2)
старых координатных осей в новой
системе.Определить общую прямую следующих двух пучков:
(2+3λ)x–(4–7λ)y+λ=0, (3–μ)x+(4–7μ)y+5=0.
Даны два параллелограмма ABCDиAMNP, гдеM– точка стороныAB,N – точка стороныAD.Доказать, что прямыеMD,BP,NCпересекаются в одной точке.
Доказать, что треугольник ABC– равнобедренный, и составить уравнение его оси симметрии: 1)A(2,1),B(4,3),C(2,3); 2)A(1,–3),B(–1,1),C(0,–1).
Прямоугольную декартову систему координат (
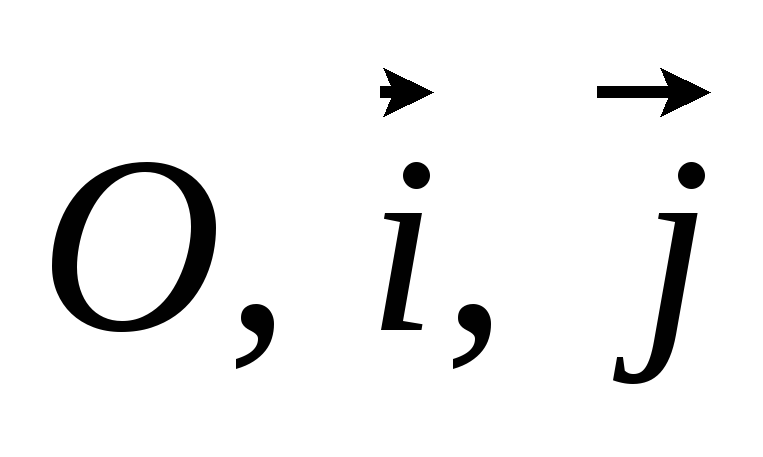 )
повернули вокруг начала координат на
угол +300. Найти уравнения: 1) новых
координатных осей в старой системе; 2)
старых координатных осей в новой
системе.
)
повернули вокруг начала координат на
угол +300. Найти уравнения: 1) новых
координатных осей в старой системе; 2)
старых координатных осей в новой
системе.
