Задачи повышенной трудности

1. Доказать, что окружность, построенная на большой оси эллипса как на диаметре, касается окружности, диаметром которой служит фокальный радиус произвольной точки эллипса.

2. Доказать, что множество центров всех окружностей, касающихся окружности и проходящих через фиксированную точку, лежащую внутри данной окружности, есть эллипс.

3. Доказать, что для любой прямой, проходящей через один из фокусов гиперболы с центром Oи пересекающей линию в точкахMиN, суммане зависит от выбора этой прямой.

Домашнее задание

1. Найти эксцентриситет эллипса, у которого сумма полуосей равна расстоянию между фокусами.

2. Через один из фокусов эллипса, заданного уравнением 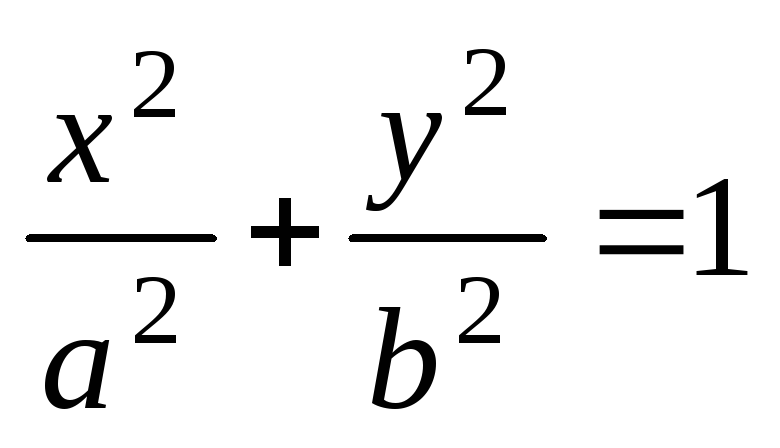, проведена хорда, параллельная оси ординат. Найти ее длину.

3. Найти сторону квадрата, вписанного в эллипс, заданного уравнением .

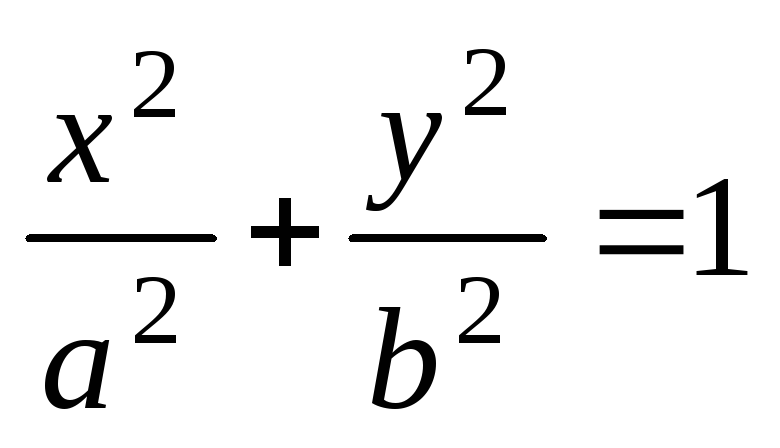Тема 3.3. Гипербола

Литература: [1], гл. 6, § 5–8, стр. 129–147; [7], гл. 4, § 28, стр. 95–100.

Основные сведения

Гиперболой называется множество всех точек плоскости (Рис. 27), абсолютное значение разности расстояний от каждой из которых до данных точек иравно длине данного отрезкаPQ, причем PQ<F₁F₂.

Точки иназываютсяфокусами гиперболы, а расстояние между ними –фокальным расстоянием.

ЕслиM– точка данной гиперболы, то отрезкиF₁MиF₂Mназываютсяфокальными радиусамиточкиM.

Уравнение называетсяканоническим уравнением гиперболы. Числаaиbназываются соответственнодействительной и мнимой полуосями гиперболы. Прямые с угловыми коэффициентами, проходящие через начало координат, называютсяасимптотами гиперболы.

Задачи

1. Составить уравнение гиперболы, фокусы которой лежат на оси ОYсимметрично началу системы координат, если:

1) Мнимая ось равна 6, гипербола проходит через точку (6,–4);

2) Уравнение асимптот и расстояние между вершинами 48;

3) Расстояние между директрисами , эксцентриситет.

2. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом и проходящей через точку.

3. Вывести условие, при котором прямая касается гиперболы:.

4. Найти множество центров окружностей, отсекающих на двух перпендикулярных прямых отрезки длинной 2и 2.

5. Докажите, что директрисы гиперболы проходят через основания перпендикуляров, опущенных из соответствующих фокусов на асимптоты. Выразите длины этих перпендикуляров через оси гиперболы.

6. Докажите, что произведение расстояний от любой точки до двух ее асимптот для данной гиперболы есть величина постоянная.

7. Докажите, что отрезок асимптоты от центра гиперболы до точки пересечения асимптоты с директрисой равен действительной полуоси гиперболы.

8. Доказать оптическое свойство гиперболы: луч света, исходящий из одного фокуса гиперболы, отразившись от нее, идет по прямой, соединяющий точку отражения с другим фокусом.

Задачи повышенной трудности

1. Доказать, что множество всех центров окружностей, касающихся данной окружности и проходящих через фиксированную точку, лежащую вне данной окружности, есть гипербола.

2. Доказать, что директриса гиперболы проходит через ортогональную проекцию соответствующего фокуса на асимптоту.

3. Доказать, что если асимптоты гиперболы имеют уравнения 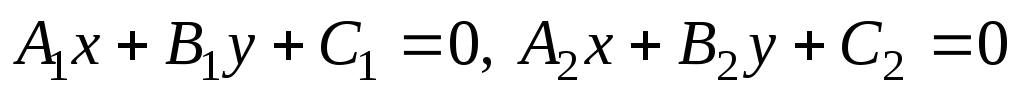, то уравнение этой гиперболы можно записать в виде.

4. Докажите, что площадь параллелограмма, одна из вершин которого лежит на гиперболе, а две стороны – на асимптотах, есть величина постоянная, равная половине произведения полуосей гиперболы.

5. Доказать, что для любой прямой, проходящей через один из фокусов гиперболы с центром Oи пересекающей линию в точкахMиN, сумма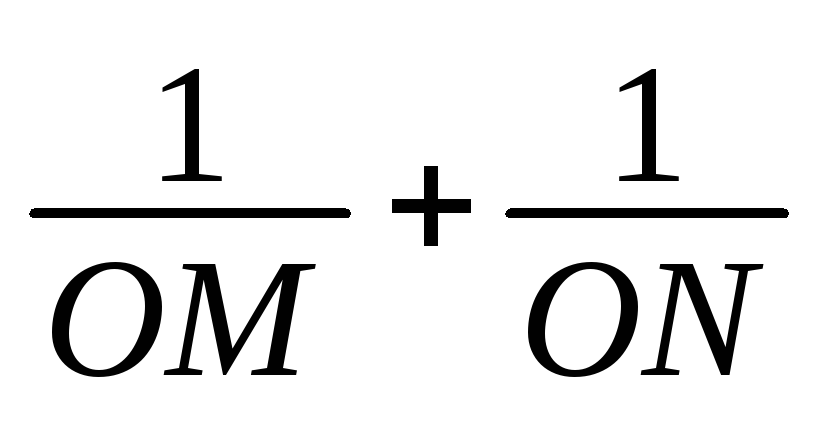не зависит от выбора этой прямой.

Домашнее задание

1. Написать уравнения асимптот и директрис гиперболы, заданной в полярной системе координат уравнением .

2. Написать уравнение гиперболы, асимптоты которой заданы уравнениями а директрисы – уравнениями.

3. Доказать, что эллипс и гипербола, имеющие общие фокусы, пересекаются под прямым углом.