Тема 2.4. Ориентация плоскости. Преобразования координат на плоскости

Литература: [1], гл. 9, § 1, стр. 207–218; [7], гл. 2, § 13,15, стр.51–54,55-59.

Основные определения, теоремы и формулы

Пусть даны два базиса B=() иB΄=(). Разложим векторы базисаB΄ по векторам базиса B: .

Матрица, где координаты вектораобразуют первый столбец, а координаты вектора– второй, называетсяматрицей перехода от базиса B к базису B΄.

Базисы B и B΄ ориентированы одинаково (противоположно), если определитель матрицы перехода положителен (отрицателен).

Рассмотрим на плоскости две аффинные системы координат R=(O,) иR΄=(O΄,). Пусть в первой системе координат точкаM имеет координаты (), а во второй – ().Формулы преобразования аффинной системы координат имеют вид:

,

где () – координаты точки O΄ в репере R. При переходе от прямоугольной системы координат R=() к прямоугольной системеR΄=(O΄,) формулы преобразования примут следующий вид: , где, еслиR и R΄ ориентированы одинаково, и , если реперы ориентированы противоположно.

Вопросы для самоконтроля

1. Какой вид имеет матрица перехода при переходе от базиса () к базису: 1) (); 2) ()?

2. Может ли определитель матрицы перехода быть равным нулю? Обоснуйте ответ.

3. Какими свойствами обладает определитель матрицы перехода от одного базиса к другому?

4. Что такое ориентация векторного пространства?

5. Какая плоскость называется ориентированной?

6. Какая система координат называется: 1) левой? 2) правой? Приведите примеры.

7. Определите понятие «направленный угол между векторами и».

8. Сформулируйте и докажите теорему о вычислении координат вектора в ортонормированном базисечерези.

9. Выведите формулы для вычисления направленного угла между двумя векторами и.

10. Сформулируйте задачу преобразования координат.

11. Запишите формулы преобразования координат и объясните смысл коэффициентов перед переменными.

12. Какие частные случаи преобразования координат можно выделить? Какой вид имеют формулы преобразования координат в каждом случае?

13. Какой вид имеют формулы преобразования координат, если одна прямоугольная система координат получена из другой вращением вокруг начала координат на угол?

Пример 1. Определить величину угла, на который повернуты оси, если формулы преобразования прямоугольной системы координат заданы равенствами;.

Решение. Как известно формулы преобразования прямоугольной системы координат имеют вид:

,, где.

Сравнив эти формулы с данными в условии задачи, получим: ,, где–величинаугла поворота осей. Так как, то угол поворота лежит вIVкоординатной четверти, тогда.

Пример 2. Даны две точкиМ(9; −3) иМ₁(−6;5). Начало координат перенесено в точкуМ, а оси координат повернуты так, что положительное направление оси абсцисс совпадает с направлением отрезкаММ₁(Рис. 20). Вывести формулы преобразования координат.

Решение.Выполним все построения, указанные в задаче: в системе координатОХУпостроим точкиМ(9; −3)иМ₁(−6;5), перенесем начало системы координат в точкуМ(9; −3), получим промежуточную систему координатМХ′′У′′, которую повернем на угол величины так, чтобы положительное направление новой оси абсциссМХ′′ совпало с направлением отрезкаМ₁Ми тем самым получим систему координатМХ′У′, координатыx′,y′ точек которой необходимо связать с координатамиx,yэтих же точек в системе координатОХУ. Координаты нового начала нам известны: из найдем

.

Тогда формулы преобразования прямоугольных координат примут вид:,.

Задачи

1. Написать формулы преобразования координат при переходе от системы координат R=(O,,) к системе, если известны координаты точкиO′ в репереRи координаты векторовв базисе (,): 1)O′(0,1),(1,1),(−3,2); 2)O′(−10,1),(−1, −1),(0,2). В каждом из случаев выясните, как ориентированы реперыRиR′ одинаково или противоположно?

2. Какие из формул, приведенных ниже, можно считать формулами преобразования аффинной системы координат?

а) ,; б);

в) .

3. Медианы AA₁иCC₁треугольникаABCпересекаются в точкеM. Даны координаты точкиD(−2,1) в системе координатR=(C, ). Найти координаты точкиDв системеR′=(M,).

4. Найти систему координат 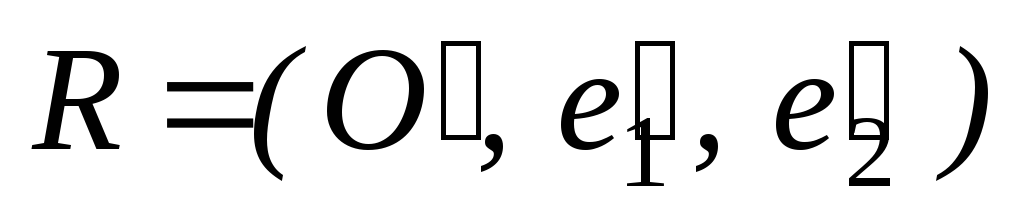, в которой линия, заданная в системеR=(O,,) уравнением, имела бы уравнение.

5. Какие из следующих формул, заданных в прямоугольной декартовой системе координат, являются формулами преобразования прямоугольных декартовых систем координат:

1. ;

2)  ; 3).

6. Фигура в прямоугольной декартовой системе координат R=(O,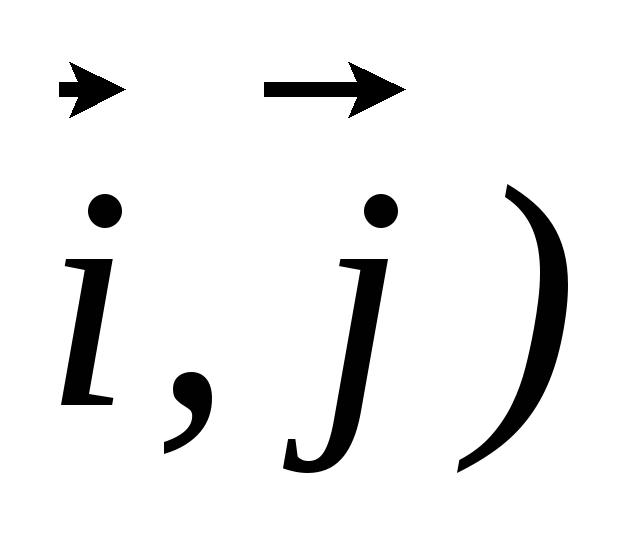задана уравнениемНайдите уравнение этой фигуры в прямоугольной системе координатR′, которая получена из репераR поворотом вокруг начала координат на угол 30⁰: 1) по часовой стрелке; 2) против часовой стрелки.

7. Как изменится уравнение линии, заданной в прямоугольной декартовой системе координат R=(O,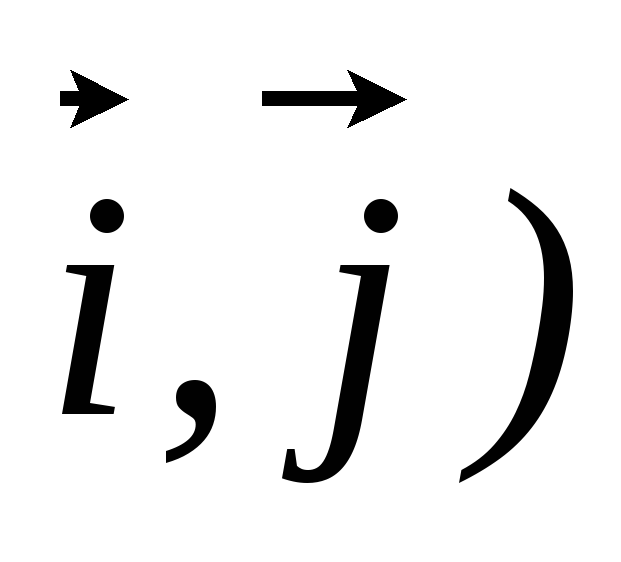уравнением, при переходе к прямоугольной декартовой системе координатR′=(O,, оси которой направлены по биссектрисам координатных углов репераR?

8. В системе координат R=(O,,) даны точкиA(2,1),B(3,0),C(1,4). Найти систему координатR′=(O′,), в которой те же точки имеют координатыA(1,6),B(1,9),C(3,1).

Домашнее задание

1. Дан параллелограмм ABCD. В системе координат (A, ) точкаE имеет координаты (). Найти координаты точкиEв системе координат (B, ).

2. Составить формулы преобразования координат при переходе от системы R=(O,к системеR′=(O,противоположной ориентации, если угол между векторамииравен 30⁰иO′(0, −2).

3. Написать формулы преобразования координат: а) при переходе от системы R=(O,,) к системеR′=(O′,), если

а) ; б) началоOсистемы переносится в точкуO′(−3,2).