Каноническое уравнение прямой

Определение. Любой вектор, отличный от нулевого, параллельный заданной прямой, называется направляющим вектором этой прямой.

Пусть на прямой задана точка, а вектор– направляющий вектор прямой. Точкапринадлежит прямой, если векторпараллелен вектору:

. (12)

Уравнение (12) называется каноническим уравнением прямой на плоскости.

Угол между прямыми, заданными каноническими уравнениями, определяется как угол между направляющими векторами этих прямых:

.

Условием параллельности прямых будет условие коллинеарности их направляющих векторов:

||.

Условие перпендикулярности прямых равносильно условию равенства нулю скалярного произведения их направляющих векторов:

.

Параметрические уравнения прямой

Пусть .

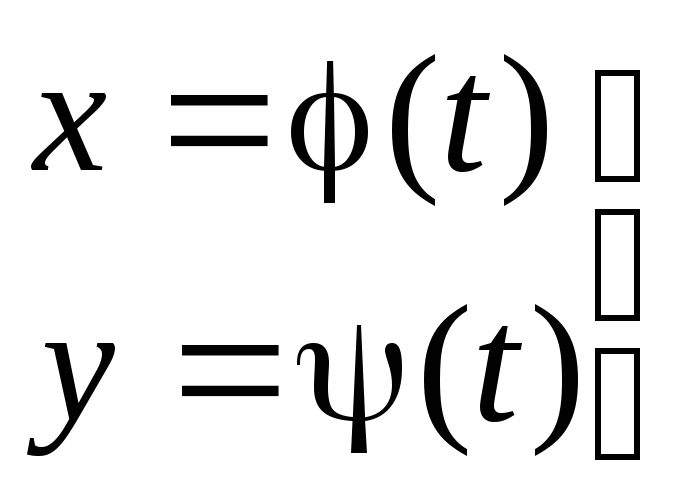Если величины х и у рассматривать как координаты точки М при каждом значении t, то такие уравнения называются параметрическими уравнениями траектории точки М. Аргумент t – переменный параметр.

В каноническом уравнении прямой (12) примем одну из величин (правую или левую часть равенства) за параметр t. Получим два уравнения

или . (13)

Уравнения (13) – это параметрические уравнения прямой на плоскости. Если принять, что параметр t – время, то параметрические уравнения приобретают физический смысл. Они определяют закон движения точки по прямой L.

Нормальное (нормированное) уравнение прямой

Пусть существует прямаяL. Проведем вектор , перпендикулярный, через начало координат.Р – точка пересечения прямой и нормали.

На нормали введем положительное направление от О к Р.

Пусть - полярный угол нормали,

–полярный угол вектора . Обозначим |ОР| = р. Выберем на прямой точкуМ(х,у). Проекция вектора на нормаль определяется как

np_n= p (14)

Найдем выражение np_n через координаты точки М. Пусть – полярные координаты точки М.

np_n=

.

np_n=(15)

Из (1) и (2) => или

(16)

Уравнение (16) – это нормальное уравнение прямой.

Расстояние от точки до прямой

Пусть М^* – любая точка плоскости, d – её расстояние от данной прямой.

Определение. Отклонением точки М* от данной прямой называется число (+d), если М* лежит по ту сторону от прямой, куда указывает положительное направление нормали, и (–d) – в обратном случае.

= ±d

Теорема. Пусть точка М* (х*, у*)произвольная точка плоскости, L – прямая, заданная уравнением xcosα + ysinα – р = 0. Отклонение точки М* от этой прямой задается формулой

. (17)

Доказательство. Проекция точки М* на нормаль – точка . Отклонение точкиМ* от прямой

δ= PQ = OQ – OP.

Но OQ = np_n, а ОР = р δ =np_n* - р

np_n= .

Таким образом, отклонение точки М* от прямой легко вычисляется, если прямая задана нормальным уравнением. Достаточно лишь подставить в нормальное уравнение прямой координаты точки.

Пусть прямая задана общим уравнением: Ах + Ву + С = 0, а

x cosα + y sinα – р = 0 – её нормальное уравнение .

Поскольку два уравнения определяют одну прямую, их коэффициенты должны быть пропорциональны. Уравнение

(18)

совпадает с нормальным уравнением. Тогда

;

.

Отсюда можно найти :

–нормирующий множитель уравнения прямой.

Определим знак нормирующего множителя:

µС = - р < 0.

Следовательно, знак µ противоположен знаку С в уравнении. (Если С = 0 – знак µ произвольный).