Нормальное уравнение плоскости. Расстояние от точки до плоскости.

Пусть существует плоскость . Проведем нормальчерез начало координат О. Пусть заданы– углы, образованные нормальюс осями координат.. Пусть– длина отрезка нормалидо пересечения с плоскостью. Считая известными направляющие косинусы нормали, выведем уравнение плоскости.

Пусть ) – произвольная точка плоскости. Вектор единичной нормали имеет координаты. Найдем проекцию вектора на нормаль.

.

Поскольку точка М принадлежит плоскости, то

.

(8)

Это и есть уравнение заданной плоскости, называющееся нормальным.

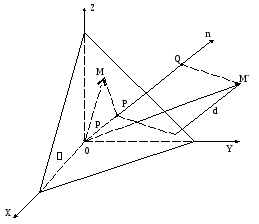
Расстояние от точки до плоскости

Пусть дана плоскость ,М*– точка пространства,d – её расстояние от плоскости.

Определение. Отклонением точки М* от плоскости называется число (+d), если M* лежит по ту сторону от плоскости, куда указывает положительное направление нормали , и число (-d), если точка расположена по другую сторону плоскости:

.

Теорема. Пусть плоскость с единичной нормальюзадана нормальным уравнением:

.

Пусть М*– точка пространства Отклонение т.M* от плоскости задаётся выражением

. (9)

Доказательство. Проекцию т. * на нормаль обозначимQ. Отклонение точки М* от плоскости равно

.

;

;

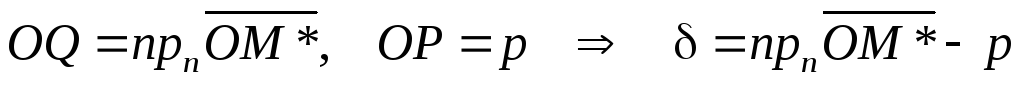(9)

Правило. Чтобы найти отклонение т. M* от плоскости, нужно в нормальное уравнение плоскости подставить координаты т. M*. Расстояние от точки до плоскости равно .

Приведение общего уравнения плоскости к нормальному виду

Пусть одна и та же плоскость задана двумя уравнениями:

- общее уравнение,

- нормальное уравнение.

Поскольку оба уравнения задают одну плоскость, их коэффициенты пропорциональны:

.

Первые три равенства возведем в квадрат и сложим:

.

Отсюда найдем – нормирующий множитель:

. (10)

Умножив общее уравнение плоскости на нормирующий множитель, получим нормальное уравнение плоскости:

.

Примеры задач на тему «Плоскость».

Пример 1. Составить уравнение плоскости , проходящей через заданную точку(2,1,-1) и параллельной плоскости.

Решение. Нормаль к плоскости :. Поскольку плоскости параллельны, то нормальявляется и нормалью к искомой плоскости. Используя уравнение плоскости, проходящей через заданную точку (3), получим для плоскостиуравнение:

Ответ:

Пример 2. Основанием перпендикуляра, опущенного из начала координат на плоскость , является точка. Найти уравнение плоскости.

Решение. Вектор является нормалью к плоскости. ТочкаМ₀ принадлежит плоскости. Можно воспользоваться уравнением плоскости, проходящей через заданную точку (3):

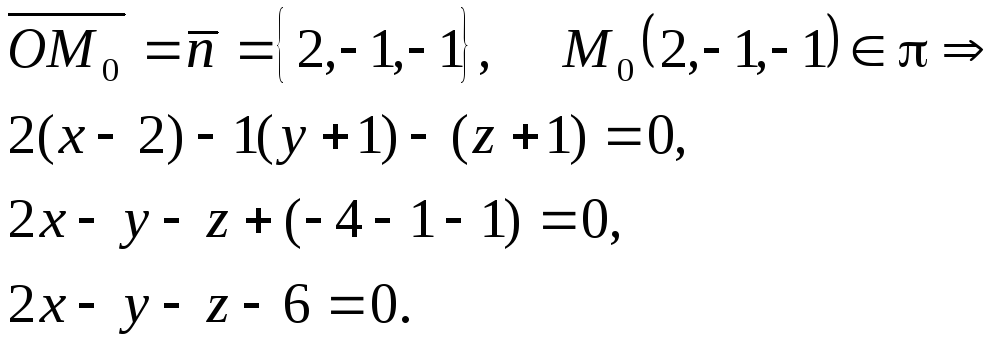
Ответ:

Пример 3. Построить плоскость , проходящую через точкии перпендикулярную плоскости :.

Следовательно, чтобы некоторая точка М (x, y, z) принадлежала плоскости , необходимо, чтобы три векторабыли компланарны:

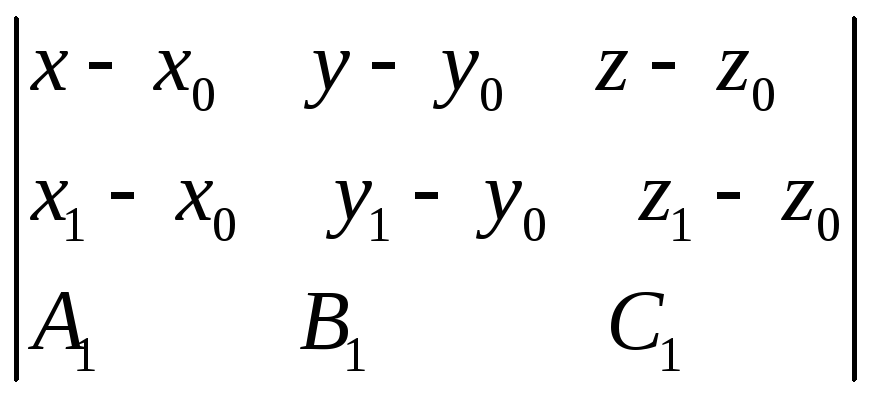=0.

Осталось раскрыть определитель и привести полученное выражение к виду общего уравнения (1).

Пример 4. Плоскость задана общим уравнением:

.

Найти отклонение точки от заданной плоскости.

Решение. Приведем уравнение плоскости к нормальному виду.

,

.

Подставим в полученное нормальное уравнение координаты точки М*.

.

Ответ: .

Пример 5. Пересекает ли плоскость отрезок.

Решение. Чтобы отрезок АВ пересекал плоскость, отклонения иот плоскостидолжны иметь разные знаки:

.

Пример 6. Пересечение трех плоскостей в одной точке.

.

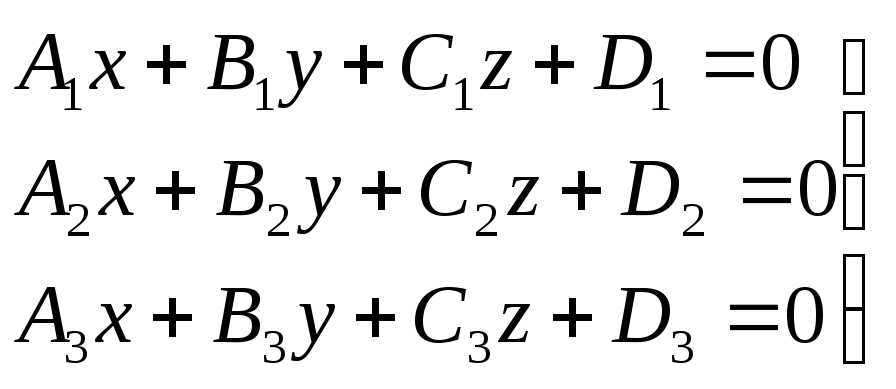
Система имеет единственное решение, следовательно, три плоскости имеют одну общую точку.

Пример 7. Нахождение биссектрис двугранного угла, образованного двумя заданными плоскостями.

Пусть и- отклонение некоторой точкиот первой и второй плоскостей.

На одной из биссектральных плоскостей (отвечающей тому углу, в котором лежит начало координат) эти отклонения равны по модулю и знаку, а на другой – равны по модулю и противоположны по знаку.

1. 

- это уравнение первой биссектральной плоскости.

2. 

- это уравнение второй биссектральной плоскости.

Пример 8. Определение местоположения двух данных точек иотносительно двугранных углов, образованных данными плоскостями.

Пусть . Определить: в одном, в смежных или в вертикальных углах находятся точкии.

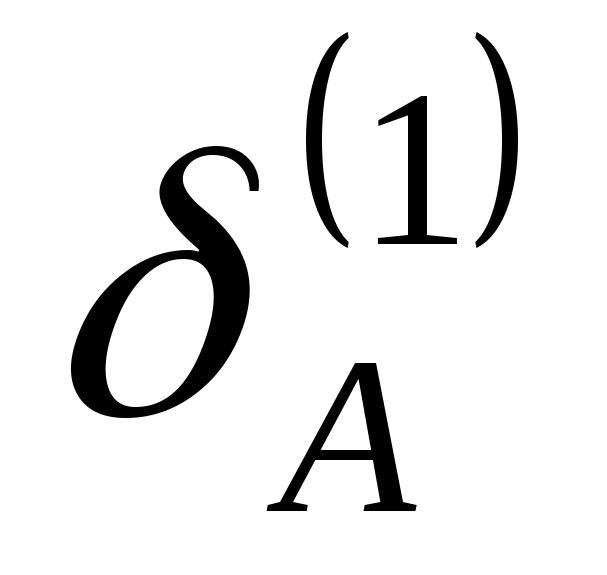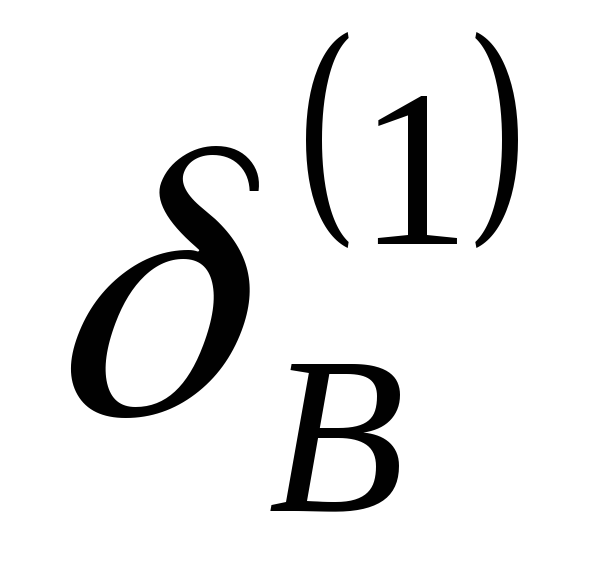1. Находим и,и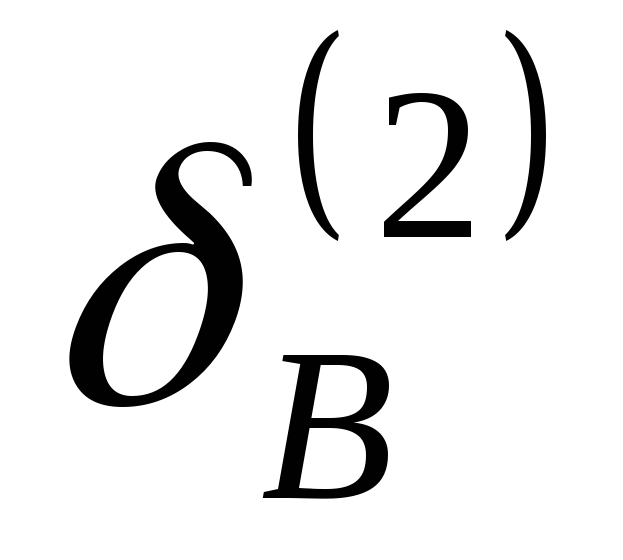- это отклонения точекА и В от плоскостей и.

а). Если илежат по одну сторону оти от, то они лежат в одном двугранном углу.

б). Если илежат по одну сторону оти по разные от, то они лежат в смежных углах.

в). Если илежат по разные стороны оти, то они лежат в вертикальных углах.

Системы координат 3

Линии на плоскости 8

Линии первого порядка. Прямые на плоскости. 10

Угол между прямыми 12

Общее уравнение прямой 13

Неполное уравнение первой степени 14

Уравнение прямой “в отрезках” 14

Совместное исследование уравнений двух прямых 15

Нормаль к прямой 15

Угол между двумя прямыми 16

Каноническое уравнение прямой 16

Параметрические уравнения прямой 17

Нормальное (нормированное) уравнение прямой 18

Расстояние от точки до прямой 19

Уравнение пучка прямых 20

Примеры задач на тему «прямая на плоскости» 22

Векторное произведение векторов 24

Свойства векторного произведения 24

Геометрические свойства 24

Алгебраические свойства 25

Выражение векторного произведения через координаты сомножителей 26

Смешанное произведение трёх векторов 28

Геометрический смысл смешанного произведения 28

Выражение смешанного произведения через координаты векторов 29

Примеры решения задач по теме: «Векторная алгебра». 30

Поверхности в пространстве 33

Плоскость 33

Неполные уравнения плоскости 35

Уравнение плоскости в «отрезках» 35

Угол между плоскостями 36

Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой 37

Нормальное уравнение плоскости. Расстояние от точки до плоскости. 38

Расстояние от точки до плоскости 39

Приведение общего уравнения плоскости к нормальному виду 40

Примеры задач на тему «Плоскость». 40

Линии в пространстве. Прямая в пространстве 46

Канонические уравнения прямой в пространстве 47

Параметрические уравнения прямой 48

Уравнения прямой, проходящей через две заданные точки 48

Угол между двумя прямыми в пространстве 49

Угол между прямой и плоскостью 49

Условие принадлежности двух прямых одной плоскости 50

Некоторые задачи на построение прямых и плоскостей 50

Примеры решения задач по теме «Аналитическая геометрия» 55

Кривые второго порядка 59

Пример приведения общего уравнения линии второго порядка к каноническому виду 59

Эллипс 62

Вывод уравнения эллипса 62

Гипербола 64

Парабола 65

Примеры решения задач на тему «Кривые второго порядка». 66