
Аналитическая геометрия
.pdfТеория для подготовки к зачету по алгебре и аналитической геометрии для
студентов I к., II семестр (заочное отделение) (специальноcть - прикладная информатика, землеустройство и кадастры)
ГЛАВА I. МЕТОД КООРДИНАТ НА ПЛОСКОСТИ.
1.Аффинная декартова система координат на плоскости и в пространстве.
2.Прямоугольнодекартовая система координат на плоскости и в пространстве.
3.Полярная система координат на плоскости.
4.Простое отношение трех точек, свойства, координатное выражение.
5.Полярносферическая система координат в пространстве.
6.Полярноцилиндрическая система координат в пространстве.
ГЛАВА II. ПРЯМАЯ НА ПЛОСКОСТИ.
7.Прямая на плоскости. Различные способы задания прямой в аффинной системе координат на плоскости.
8.Уравнение прямой, заданная точкой и направляющим вектором.
9.Уравнение прямой, проходящей через две различные точки.
10.Параметрические уравнения прямой.
11.Уравнение прямой в « отрезках».
12.Общее уравнение прямой.
13.Прямая в прямоугольнодекартовой системе координат. Способы задания прямой. Уравнение прямой, заданной точкой и нормальным вектором.
14.Нормальное уравнение прямой.
15.Расстояние от точки до прямой.
ГЛАВА III. ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ.
16.Векторное произведение векторов , свойства 1-2.
17.Векторное произведение векторов, свойство 3.
18.Координатное выражение векторного произведения.
19.Вычисление площади параллелограмма и треугольника.
20.Смешанное произведение векторов и его свойства.
21.Смешанное произведение векторов в координатах.
22.Вычисление объема параллелепипеда и тетраэдра.
ГЛАВА IV. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ.
23.Плоскость в пространстве, различные способы задания плоскости.
24.Уравнения плоскости заданной точкой и направляющим подпространством.
25.Уравнение плоскости проходящей через три точки.
26.Параметрические уравнения плоскости.
27.Уравнение плоскости в «отрезках».
28.Общее уравнение плоскости.
29.Плоскость в прямоугольно – декартовой системе координат. Способы задания.
30.Уравнение плоскости, заданной точкой и нормальным вектором.
31.Нормальное уравнение плоскости. Нормирование общего уравнения плоскости.
ГЛАВА V. ПРЯМАЯ В ПРОСТРАНСТВЕ.
32.Прямая в пространстве, различные способы задания прямой.
33.Каноническое уравнение прямой.
34.Уравнение прямой, проходящей через две различные точки.
35.Параметрические уравнения прямой.
36.Прямая как линия пересечения двух плоскостей.
ГЛАВА VI. МЕТРИЧЕСКИЕ ЗАДАЧИ НА СОЧЕТАНИЕ ПРЯМОЙ И ПЛОСКОСТИ.
37.Расстояние от точки до прямой.
38.Расстояние от точки до плоскости.
39.Расстояние между двумя параллельными плоскостями.
40.Угол между двумя плоскостями.
41.Угол между двумя прямыми.
42.Угол между прямой и плоскостью.
ГЛАВА VII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ.
43.Эллипс: определение, каноническое уравнение.
44.Свойства эллипса, эксцентриситет, зависимость формы эллипса от эксцентриситета.
45.Построение эллипса, параметрические уравнения эллипса.
46.Гипербола: определение, каноническое уравнение.
47.Свойства гиперболы, эксцентриситет, зависимость формы гиперболы от эксцентриситета.
48.Построение гиперболы, параметрические уравнения гиперболы.
49.Парабола: определение, каноническое уравнение.
50.Свойства параболы.
51.Общее уравнение кривой второго порядка.
52.Классификация кривых второго порядка на плоскости.
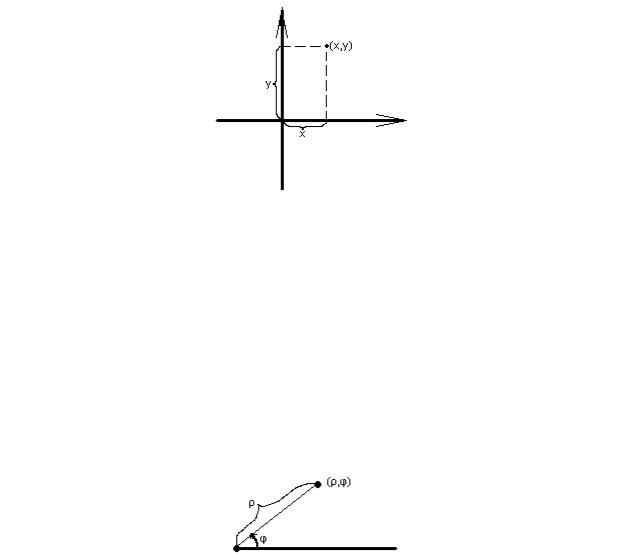
Системы координат
Декартова система координат на плоскости Декартова система координат хорошо известна. И всѐ же сформулируем
подробнее, каким образом она задаѐтся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.
Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а вовторых, две перпендикулярные направленные оси (так называемые, оси координат). Причѐм, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.
Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).
§ 2. Полярная система координат на плоскости Для того, чтобы задать полярную систему координат на плоскости, надо
зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.
Положение точки на плоскости задаѐтся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.
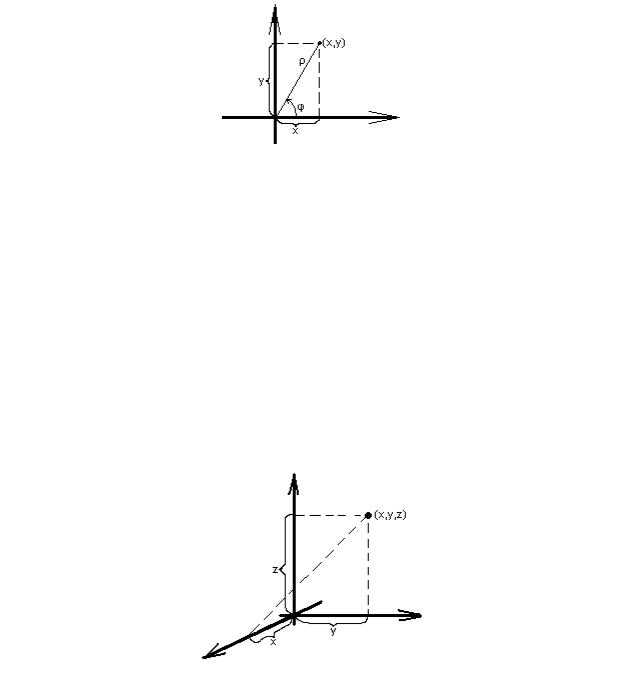
Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ 0.
0.
Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то
x= ρ∙cosφ,
y= ρ∙sinφ.
В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.
С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..
В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.
§3. Декартова система координат в пространстве Декартовы координаты в пространстве задаются с помощью точки начала
координат и трѐх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
§4. Цилиндрическая система координат в пространстве
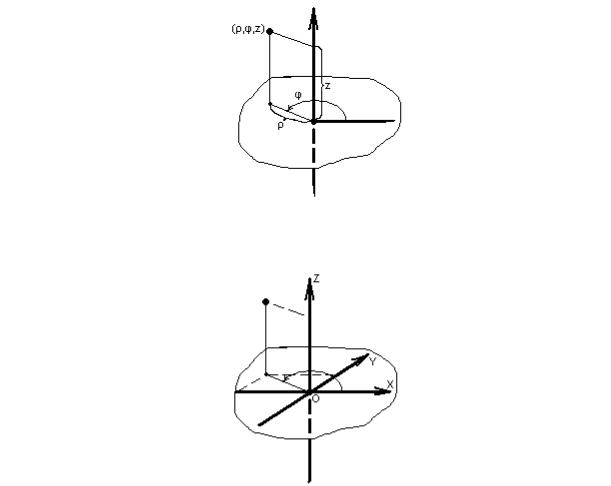
Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось.
Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображѐнном на рисунке, формулы перехода такие:
x = ρ·cosφ, y = ρ·sinφ, z = z.
§5. Сферическая система координат в пространстве Сферическая система координат вводится следующим образом: фиксируем
плоскость, на ней -- точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаѐтся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.
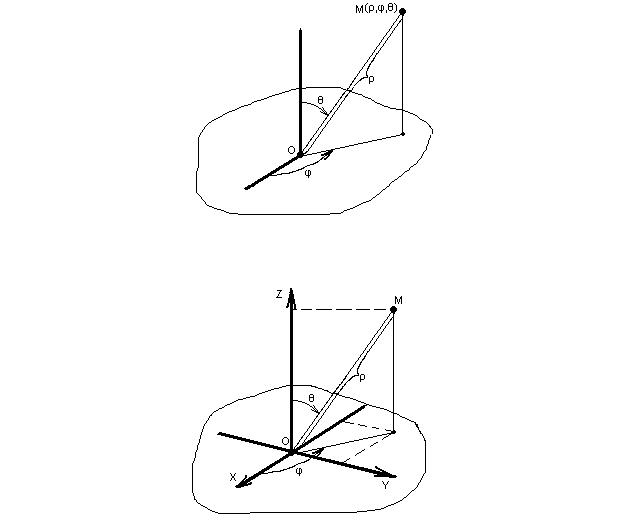
Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображѐнном на рисунке, формулы перехода такие:
x = ρ·sinθ·cosφ, y = ρ·sinθ·sinφ, z = ρ·cosθ.
Линии на плоскости ...................................................................................................................... |
8 |
Линии первого порядка. Прямые на плоскости........................................................................ |
10 |
Угол между прямыми.................................................................................................................. |
12 |
Общее уравнение прямой ........................................................................................................... |
13 |
Неполное уравнение первой степени ........................................................................................ |
13 |
Уравнение прямой “в отрезках”................................................................................................. |
14 |
Совместное исследование уравнений двух прямых................................................................. |
14 |
Нормаль к прямой........................................................................................................................ |
15 |
Угол между двумя прямыми ...................................................................................................... |
16 |
Каноническое уравнение прямой............................................................................................... |
16 |
Параметрические уравнения прямой......................................................................................... |
17 |
Нормальное (нормированное) уравнение прямой.................................................................... |
18 |
Расстояние от точки до прямой.................................................................................................. |
18 |
Уравнение пучка прямых............................................................................................................ |
20 |
Примеры задач на тему «прямая на плоскости» ...................................................................... |
21 |
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Линии на плоскости
Пусть х и у – две произвольные переменные.
Определение: Соотношение вида F(x,y)=0 называется уравнением, если оно справедливо не для всяких пар чисел х и у.
Пример: 2х + 7у – 1 = 0 , х2 + y2 – 25 = 0.
Если равенство F(x,y)=0 выполняется для любых х, у, то, следовательно,
F(x,y) = 0 – тождество.
Пример: (х + у)2 - х2 - 2ху - у2 = 0
Говорят, что числа х0 и у0 удовлетворяют уравнению, если при их подстановке в это уравнение оно обращается в верное равенство.
Важнейшим понятием аналитической геометрии является понятие уравнения линии.
Определение: Уравнением данной линии называется уравнение F(x,y)=0,
которому удовлетворяют координаты всех точек, лежащих на этой линии, и
не удовлетворяют координаты никакой из точек, не лежащих на этой линии.
Линия, определяемая уравнением y = f(x), называется графиком функции f(x). Переменные х и у – называются текущими координатами, т. к.
являются координатами переменной точки.
Несколько примеров определения линий.
1) х – у = 0 => х = у. Это уравнение определяет прямую:
у
х
2)х2 - у2 = 0 => (х-у)(х+у) = 0 => точки должны удовлетворять либо уравнению х - у = 0, либо уравнению х + у = 0, что соответствует на плоскости паре пересекающихся прямых, являющихся биссектрисами координатных углов:
у
х
3)х2 + у2 = 0. Этому уравнению удовлетворяет только одна точка О(0,0).
4)ρ=а cosθ. Это уравнение задает окружность, имеющую радиус-вектор с ,
наклоненный под углом и к оси Ох.
М
ρ
θ |
x |
О а А
Предметом изучения аналитической геометрии являются
алгебраические линии – это такие линии, которые в декартовой
прямоугольной |
системе координат определяются уравнением вида: |
|||
A x k1 |
y l1 |
A x k2 |
y l2 |
0 . |
1 |
|
2 |
|
|
Примеры: Ах+Ву+С=0,
Ах2+Ву2+Сху+Dх+Еу+F=0
Уравнение Ах+Ву+С=0 – общее уравнение первой степени.
Примеры неалгебраических линий: y - sinx = 0,
Ах + Ву + С = 0.
Определение: Линия, определяемая в декартовой системе координат алгебраическим уравнением n-ой степени, называется линией n-ого порядка.
Теорема: Если в декартовой системе координат линия определяется уравнением n-ой степени, то в другой декартовой системе координат она
также определяется уравнением n-ой степени, т. е. порядок линии не зависит от выбора системы координат.
Линии первого порядка. Прямые на плоскости.
Пусть задана декартова система координат и некоторая прямая; α – угол наклона прямой к оси Ох.
Определение: Тангенс угла α наклона прямой к оси Ох называется угловым коэффициентом этой прямой: k = tgα.
у |
|
|
|
|
М2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
М1 |
α |
у2-у1 |
|
|
|
|
|
|
|
||
α |
|
|
|
|
|
|
|
O |
|
|
|
|
х2-х1 |
х |
|
|
|
|
|
|
|
||
tg |
= |
y |
2 |
y1 |
k |
(1) |
|
x2 |
x1 |
||||||
|
|
|
|
||||
Формула (1) – определение углового коэффициента по известным двум точкам прямой.
Пусть прямая, неперпендикулярная оси Ох, имеет угловой коэффициент k и отсекает на оси Оу отрезок ОВ= b.
y
M
y-b
Bα
αb
O |
x |
x |
|
|
