Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Башкирская академия комплексной безопасности предпринимательства
Кафедра Информационной безопасности
Аналитическая геометрия. Содержание:
Векторная алгебра 3
Задачи для самостоятельной работы 8
Аналитическая геометрия 9
2.1. Прямая на плоскости 10
Задачи для самостоятельной работы 16
2.2. Прямая и плоскость в пространстве. Различные виды задания уравнений плоскости в пространстве. Прямая в пространстве. Взаимное расположение плоскостей 17
Плоскость в пространстве 17
Прямая в пространстве 19
Задачи для самостоятельной работы 23
2.3. Канонические уравнения кривых 2-го порядка (эллипс, гипербола, парабола) 24
Задачи для самостоятельной работы 27
2.4. Взаимное расположение кривых и прямых на плоскости 28
Задачи для самостоятельной работы 28
2.5. Поверхности второго порядка 29
Задачи для самостоятельной работы 32
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ 34
1. Задание по теме «Векторы. Линейные операции над векторами» 34
2. Задание по теме «Прямая на плоскости» 36
3. Задание по теме «Кривые второго порядка» 37
4. Задание по теме «Прямая и плоскость в пространстве» 44
5. Задание по теме «Поверхности второго порядка» 45
Литература 46
Основная 47
Дополнительная 47
Векторная алгебра
Определение 1.1.
Вектором
называется
направленный отрезок, концы которого
упорядочены: А – начало вектора, В –
конец вектора.
Если координаты начала и конца А(а1, а2, а3) и В(b1, b2, b3), то координаты вектора определяются следующим образом:
.
Длина вектора определяется по формуле:
.
Определения 1.2.
Векторы
и
называются коллинеарными, если они
лежат на одной или параллельных прямых.
Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Три вектора в пространстве называются компланарными, если существует плоскость, которой они параллельны.
Пример 1.1.
Даны
две точки А(1;2;3), В(4;5;6). Найти длины
векторов
и
.
Решение.
Координаты
вектора
,
а вектора
.
Длина векторов
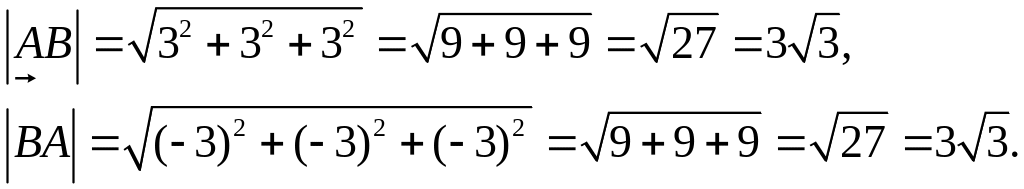
Вектора коллинеарны, противоположно направлены, длины их равны.
Определение 1.3.
Пусть
даны вектора
:
.
Тогда
вектор
называется суммой векторов
.
Обозначение:
.
Правила сложения
а) правило треугольника б) правило параллелограмма
Определение 1.4.
Произведением
вектора
на число
называется вектор
,
удовлетворяющий следующим условиям:
векторы и сонаправлены, если
и
противоположно
направлены, если
;
.
Обозначение:
.
Свойства векторов
1. + = + ;
2.
(
+
)
+
=
+ (
+
);
3.
;
4.
;
5.
.
Определение 1.5.
Скалярным
произведением двух векторов
и
называется число, определяемое равенством
,
где φ – угол между векторами и .
Пример 1.2.
Даны два вектора АВ=(5;3;4), ВА=(3;0;-3). Найти угол между векторами.
Решение.
Скалярное произведение векторов
.
Найдем
угол между векторами. Для этого найдем
длины векторов
Следовательно, угол будет равен
Пример 1.3.
Дано
|
|=2,
|
|=3
и φ=(a,b)=4π/3.
Найти модуль вектора
Решение.
Определение 1.6.
Векторным произведением двух векторов и называется вектор , длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам и так, что векторы , и образуют правую тройку.
.
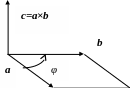
Геометрически
равен площади S
параллелограмма, построенного на
векторах
и
.
Пример 1.4.
Найти площадь треугольника, вершины которого заданы координатами А(1,0,2), В(-2,1,3), С(2,3,4).
Решение.
Вектора АВ=(-3;1;1), АС=(1;3;2). Векторное произведение векторов АВ и АС:
Определение 1.7.
Смешанное произведение трех векторов , и есть число, равное
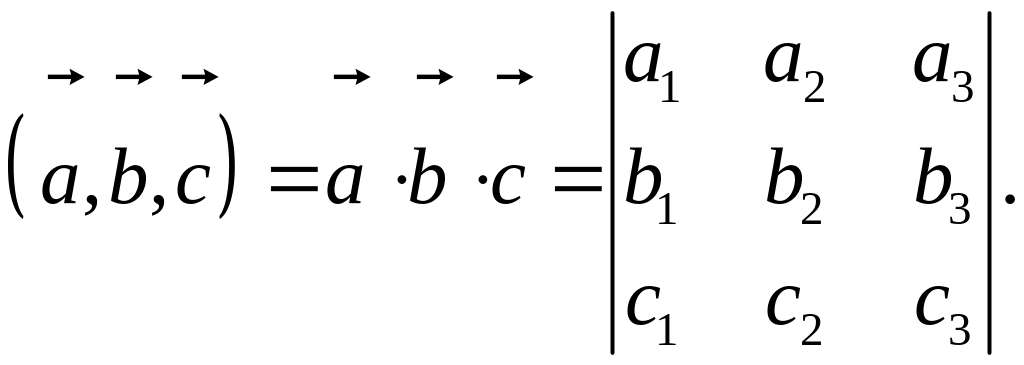
Геометрически модуль смешанного произведения равен объему V параллелепипеда, построенного на векторах , и .
Определение 1.8.
Базисом на прямой называется любой ее ненулевой вектор.
Базисом на плоскости называется любая пара неколлинеарных векторов.
Базисом в пространстве называется любая тройка некомпланарных векторов.
Например, (i, j, k) – базис в пространстве xOyz. Тогда любой вектор можно разложить по данному базису:
Некоторые метрические формулы
1)
.
2)
Пусть
,
.
Если
.
3)
Из формулы косинуса угла между векторами
легко найти углы ,
,
,
которые вектор
образует с осями координат. Эти углы
называются направляющими
углами.
Так
как
,
то имеем:
,
,
.
,
,
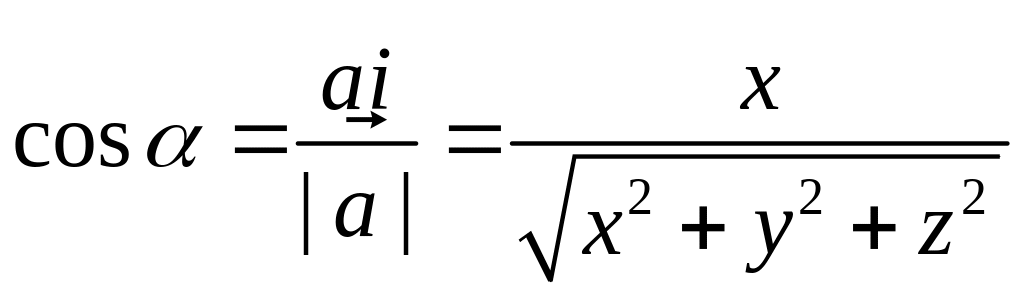называются направляющими косинусами
вектора
.
Они связаны соотношением
.
Следовательно,
вектор
есть координаты вектора, называемого
ортом
(вектора
,
обладающего условиями:
и
).
.
Пример 1.5.
Даны на координатной плоскости xOy вершины A(-1; 1), B(5; 4), C(2; 5) треугольника.
Найти:
1) длину и уравнение каждой из трёх сторон ΔABC;
2) внутренний угол A в радианах с точностью до 0,001;
Сделать чертёж.
1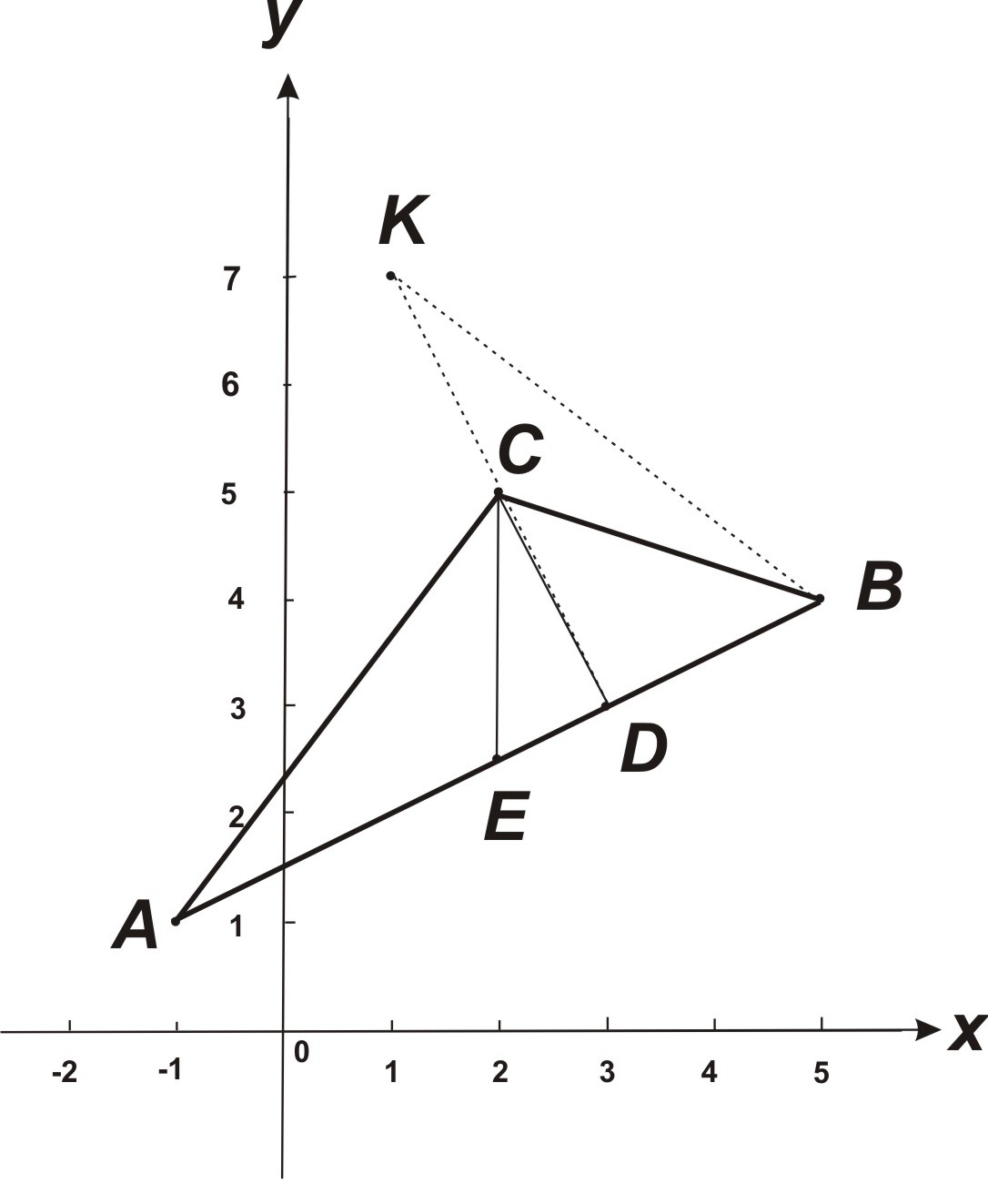
)
найти длину и уравнение сторон
длины сторон
,
уравнения сторон через две точки:
AB:
3x + 3 = 6y - 6; x - 2y + 3 = 0 общее уравнение AB
-x + 2 = 3y-15; x + 3y - 17 = 0 общее уравнение BC
-4x + 8 = -3y + 15; 4x - 3y + 7 = 0 общее уравнение AC
2) угол A в радианах
.
