Гипербола

О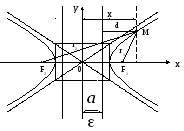пределение. Гипербола– геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная большой оси гиперболы.

Эта разность по модулю должна быть меньше расстояния между фокусами и отлична от нуля.

и - фокусные радиусы точки.

(по определению) следовательно .

Гипербола состоит из двух отдельных частей, называемых ветвями.

Канонический вид уравнения

, (11)

следовательно,

.

Уравнение – это уравнение прямой с угловым коэффициентом. При.

Прямые называютсяасимптотамигиперболы.

Отрезки и- оси гиперболы.

Уравнение вида задает гиперболу, сопряженную с первой.

Гипербола с равными полуосями называется равносторонней:

Определение.Эксцентриситетомгиперболы называется отношение расстояния между фокусами к расстоянию между вершинами:

. (12)

Определение.Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, расположенные симметрично относительно центра на расстоянииот него, называютсядиректрисамигиперболы.

Теорема.Для любой точки эллипса и гиперболы справедливо соотношение

, (13)

где – расстояние от точки до фокуса, а– расстояние до соответствующей директрисы.

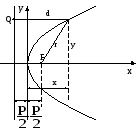
Парабола

Определение.Парабола– это геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой:

. (14)

–фокус, – расстояние от фокуса до директрисы – параметр параболы,– фокальный радиус точки.

(15)

– каноническое уравнение параболы, симметричной относительно оси О, приветви параболы направлены вправо. Уравнение

задает параболу, симметричную относительно оси ординат, ветви которой при направлены вверх.

Примеры решения задач на тему «Кривые второго порядка».

Пример 1: Найти координаты фокусов и эксцентриситет эллипса

Решение: Для данного эллипсаи поэтому

Следовательно, фокусы имеют координаты и, эксцентриситет

Пример 2: Найти полуоси, координаты фокусов и эксцентриситет эллипса

Решение: Разделив на 36, приведем данное уравнение к виду

Отсюда следует, что большая полуось эллипса , а малая полуось. При этом ось эллипса и его фокусы расположены на оси. Найдемпо формуле

.

Следовательно, координаты фокусов и, а его эксцентриситет

Пример 3: Составить каноническое уравнение эллипса, зная, что его большая полуось, а его эксцентриситет. Найти расстояние между фокусами эллипса.

Решение: Воспользуемся формулой, выражающей эксцентриситет через отношение полуосей:

, или , откуда.

В данном случае

Следовательно, каноническое уравнение эллипса

.

Так как , то;и расстояние между фокусами

Пример 4: Асимптоты гиперболы имеют уравнения, а расстояние между фокусами равно 20. Написать ее каноническое уравнение.

Решение: Разрешим уравнения асимптот относительнои, сравнив с общей формулой асимптот, найдем отношениек:

Кроме того, , т.е. . Так как для гиперболы, то для нахожденияиполучим систему уравнений

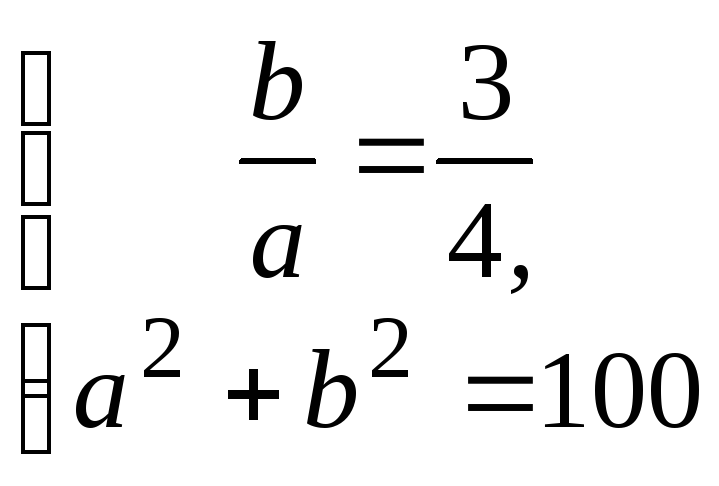
решая которую, найдем . Следовательно, каноническое уравнение гиперболы имеет вид

Пример 5: Парабола с вершиной в начале координат проходит через точкуи симметрична относительно оси. Написать ее уравнение.

Р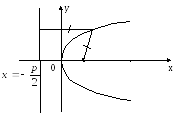ешение:Так как парабола симметрична относительно осии проходит через точкус положительной абсциссой, то она имеет вид, представленный на рис.

Подставляя координаты точки в уравнение такой параболы, получим, т.е..

Следовательно, искомое уравнение

фокус этой параболы , уравнение директрисы