Плоскость

Теорема. В декартовой системе координат каждая плоскость определяется уравнением первой степени. И обратно: в декартовой системе координат каждое уравнение первой степени определяет плоскость.

Доказательство. Пусть существует произвольная плоскость . Пусть точка. Пусть задан вектор. Пусть– произвольная точка пространства с переменными координатами. Условие принадлежности точкиМ плоскости – это перпендикулярность векторови:

.

Выразим условие принадлежности т. к плоскостичерез координаты векторови.

Условие перпендикулярности векторов:

(*)

– это и есть уравнение плоскости , поскольку ему удовлетворяют только точки плоскости. Преобразуем его:

= 0 или

. (1)

Уравнение (1) – это общее уравнение плоскости. Таким образом, плоскостьдействительно определяется уравнением первой степени.

Докажем второе утверждение. Пусть дано произвольное уравнение первой степени (1): .

Пусть - решение данного уравнения .

Тогда равенство – тождество. (2)

Вычтем тождество (2) из уравнения (1), получим

. (3)

Это уравнение плоскости, проходящей через заданную точку и имеющей нормаль(см. уравнение (*)).

Уравнение (1) равносильно уравнению (3), т. к. они получаются друг из друга путем почленного вычитания тождества. Следовательно, уравнение (1) является уравнением той же плоскости. Теорема доказана.

Рассмотрим два общих уравнения плоскостей. Пусть они определяют одну и ту же плоскость (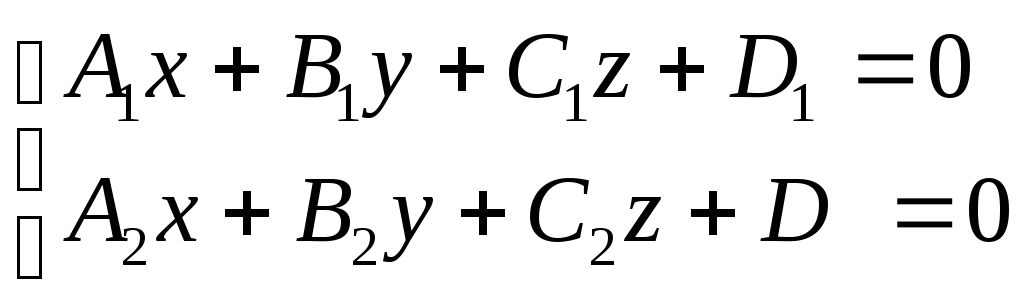4)

Тогда нормали иколлинеарны, а, следовательно, коэффициенты уравнений пропорциональны:.

Умножим первое уравнение системы на и вычтем его из второго уравнения. Получим:.

Вывод. Если два уравнения определяют одну и ту же плоскость, то их коэффициенты пропорциональны.

Неполные уравнения плоскости

Неполные уравнения получаются, когда какие-либо коэффициенты уравнения равны нулю.

1. D=0, – плоскость проходит через начало координат.

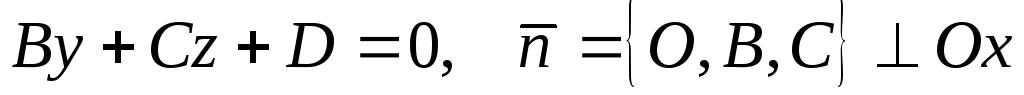2. A=0, , плоскость параллельна осиОх.

3. B=0, плоскость параллельна оси .

4. С=0, плоскость параллельна оси .

5. A=0, B=0 плоскость параллельна плоскости .

6. A=0, C=0 плоскость параллельна плоскости .

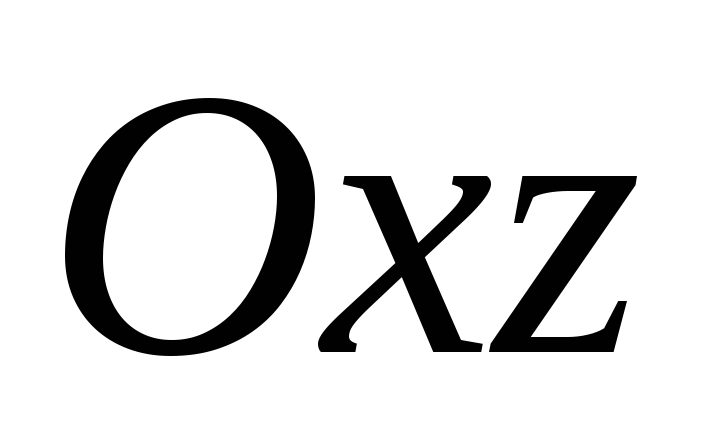7. B=0, C=0 плоскость параллельна плоскости .

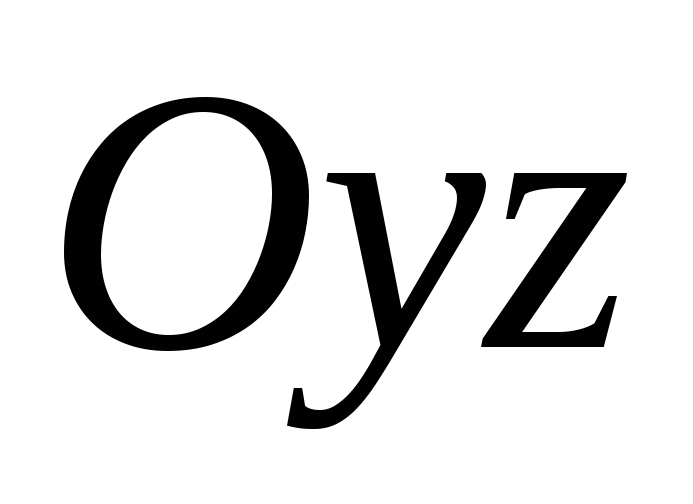8. A=B=D=0 Это плоскость .

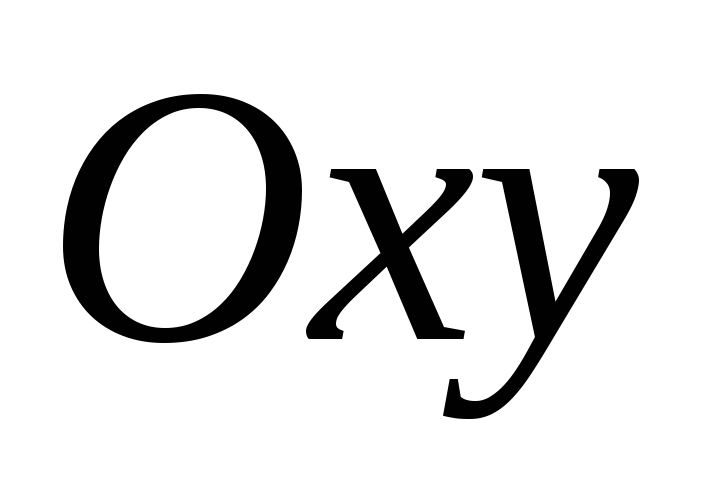9. A=C=D=0 Плоскость .

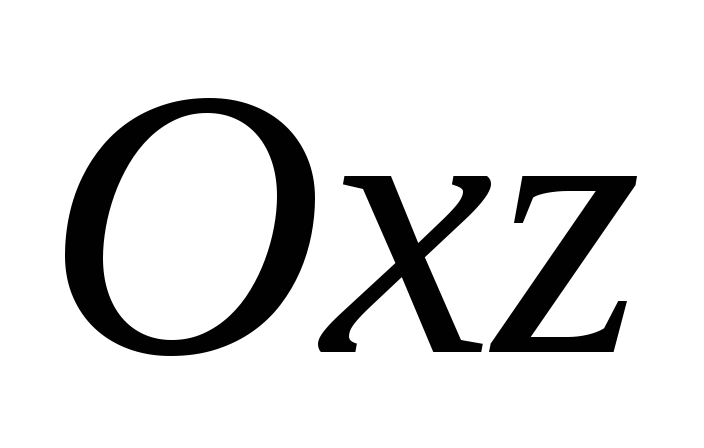10. B=C=D=0 Плоскость .

Уравнение плоскости в «отрезках»

Пусть дано общее уравнение плоскости. Преобразуем это уравнение, разделив его на (-D):

,

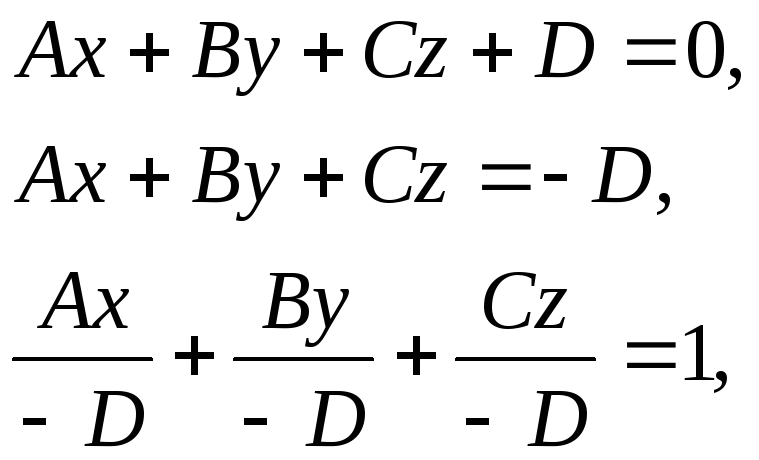
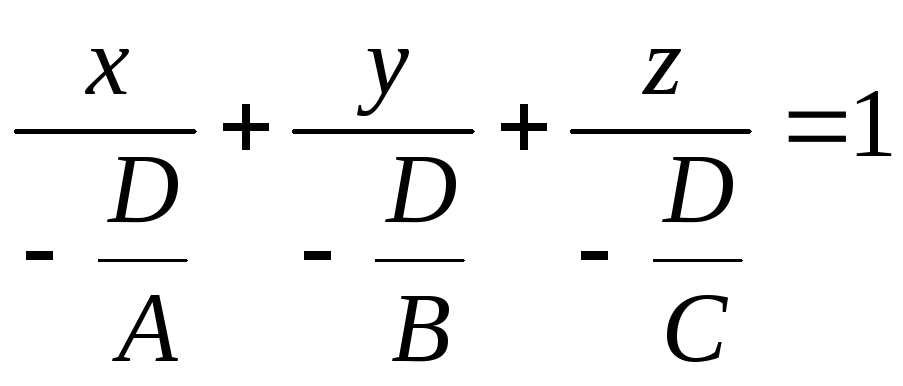. (5)

Уравнение (5) – это уравнение плоскости «в отрезках». Коэффициенты a, b, с определяют отрезки, отсекаемые плоскостью на координатных осях.

Угол между плоскостями

Пусть заданы две плоскостии , имеющие нормали соответственно. Угол между плоскостями определяется как угол между нормалями к этим плоскостям.

. (6)

Условие параллельности двух плоскостей – это условие коллинеарности нормалей:

.

Условие перпендикулярности плоскостей – это перпендикулярность нормалей:

.

Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой

Даны три точки, не лежащие на одной прямой: ,. Пусть – произвольная точка пространства.

Точка принадлежит плоскости () тогда и только тогда, когда векторыкомпланарны.

Условие компланарности трех векторов – это равенство нулю их смешанного произведения:

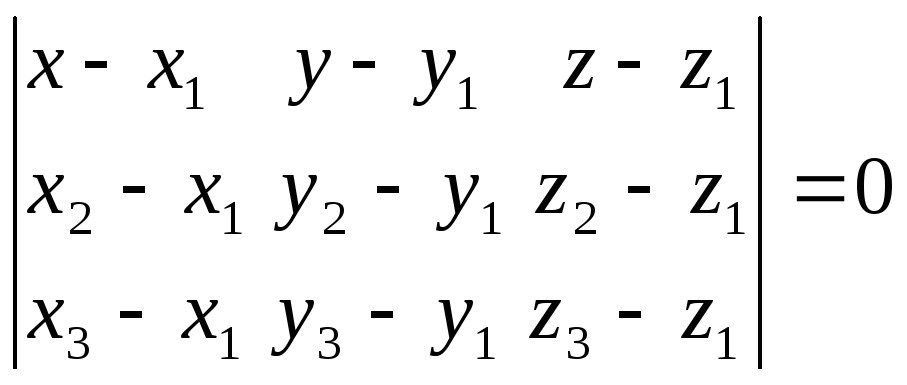. (7)

Уравнение (7) – это уравнение плоскости, проходящей через три заданные точки