Кривые второго порядка

Общее уравнение кривой второго порядка в декартовой системе координат имеет вид

,

A, B, C– одновременно не равны нулю.

Важнейшие случаи общего уравнения кривой II порядка.

1. Эллипс: 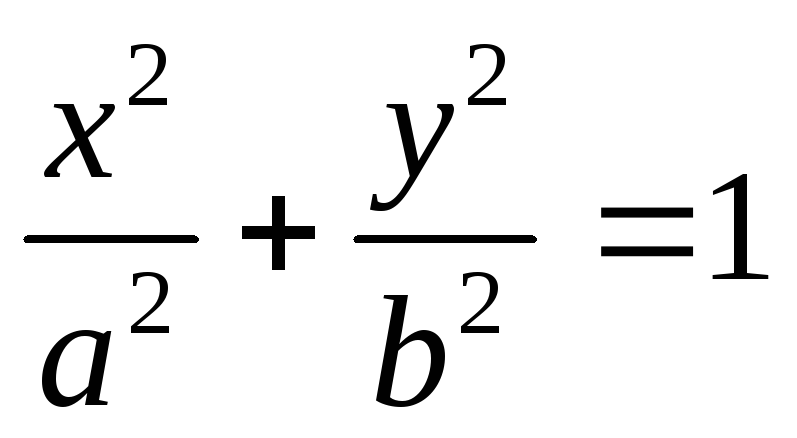, (). При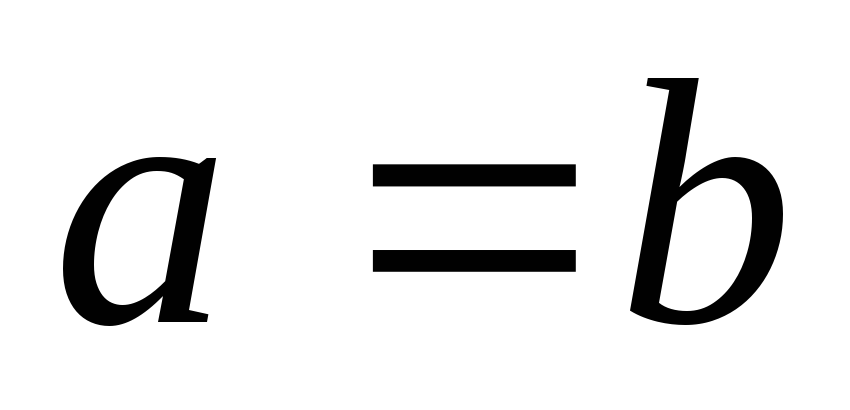- окружность.;

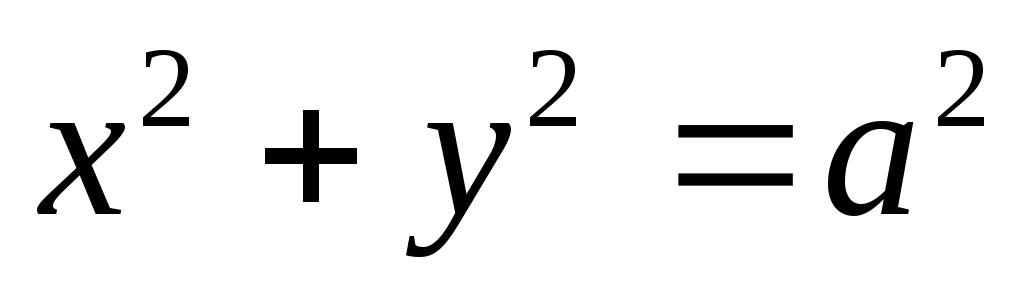2. Гипербола: 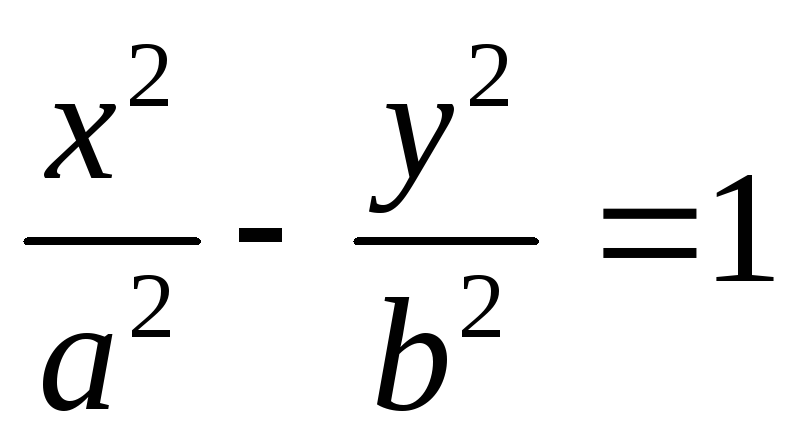, (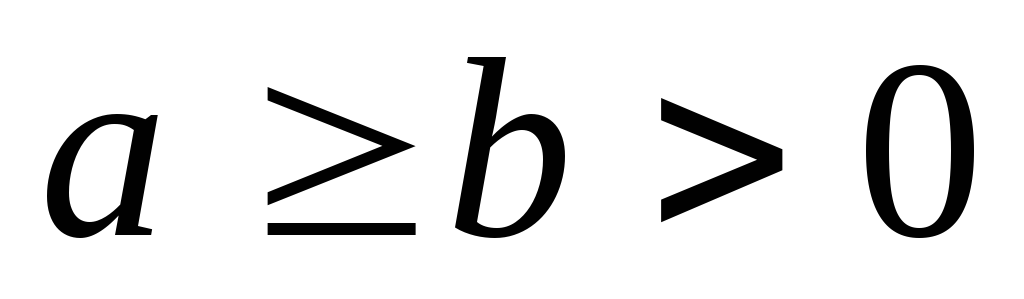) с полуосямии;

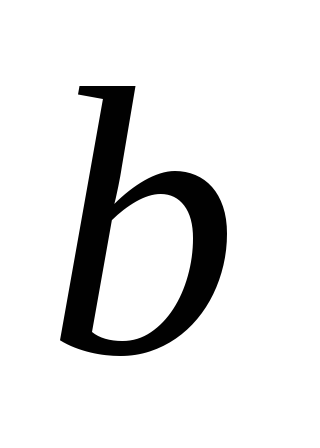3. Парабола: , ();

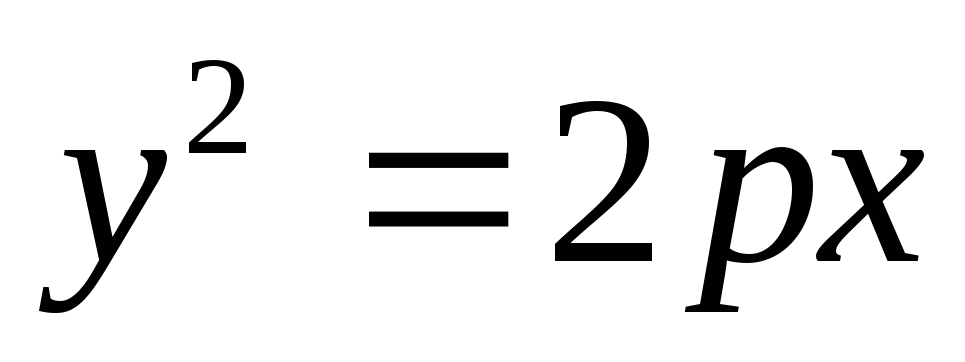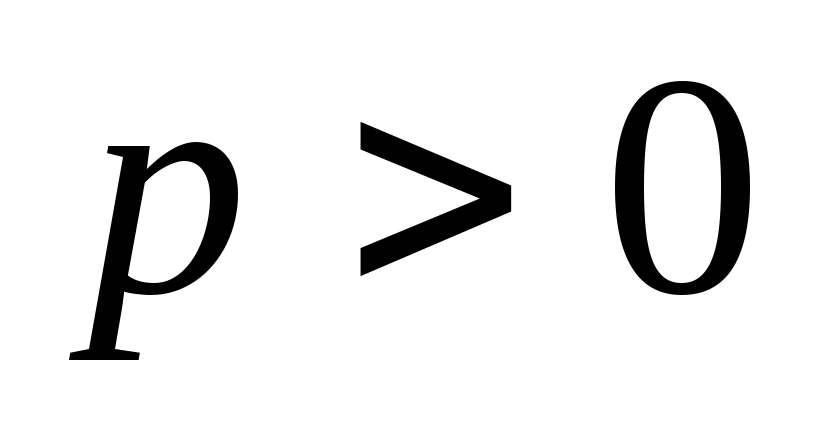4. Пара пересекающихся прямых: , ()

, ;

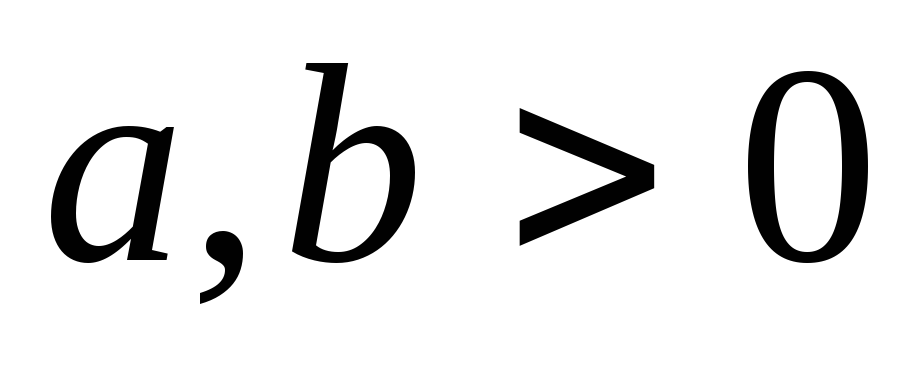5. Пара параллельных или совпадающих прямых: , ()

;

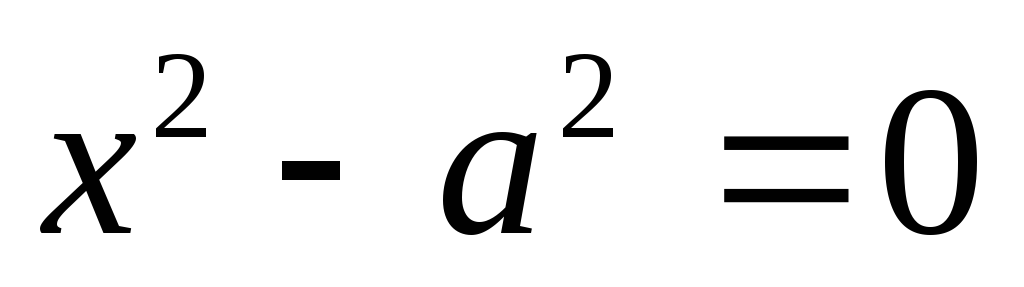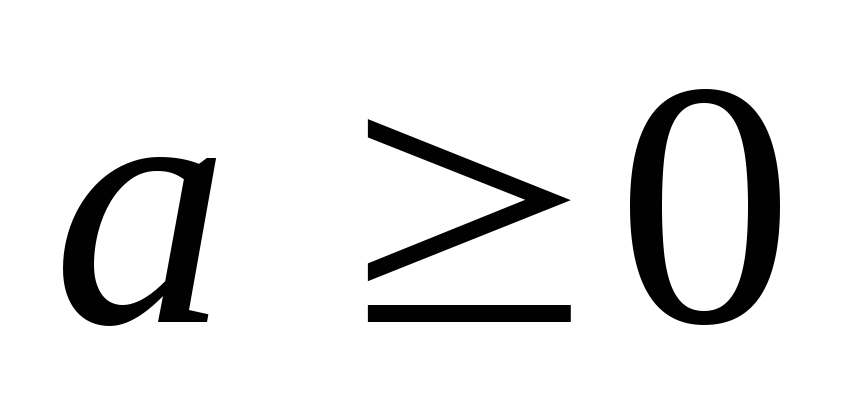6. Точка: .

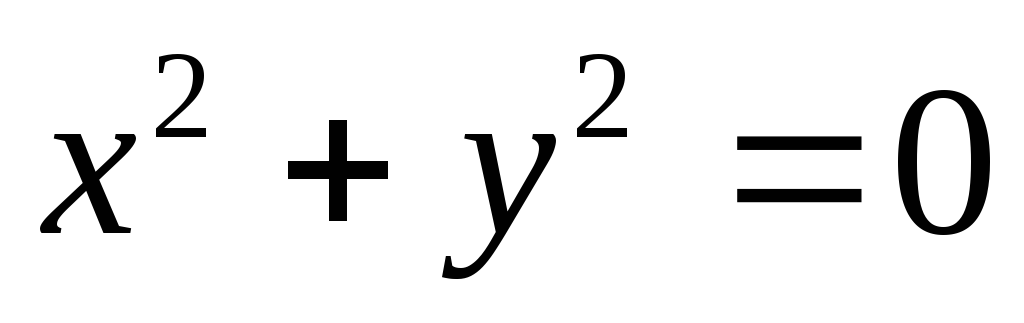Могут быть случаи, когда нет точек, удовлетворяющих уравнению:

- мнимая кривая IIпорядка (эллипс мнимый);

- пара мнимых параллельных прямых.

Пример приведения общего уравнения линии второго порядка к каноническому виду

(*)

В большинстве формул теории линий второго порядка коэффициенты входят деленными на 2, т. е. буквыобозначают половину коэффициента. Первые три члена уравнения называются старшими членами.

Можно записать уравнение (*) следующим образом:

Пусть дано общее уравнение IIпорядка (*). Требуется упростить это уравнение путём перехода к другой системе координат (с более выгодным расположением осей):

1. добиться, чтобы число членов первой степени стало наименьшим;

2. в группе старших членов избавиться от слагаемого с произведением координат;

3. избавиться от свободного члена.

Для этого воспользуемся параллельным переносом и поворотом координатных осей.

Выведем формулы преобразования координат при параллельном переносе и повороте осей. Пусть точка имеет координатыв «старой системе координат» и– в новой системе координат, полученной путем параллельного переноса и последующего поворота осей.

П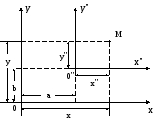араллельный перенос координатных осей

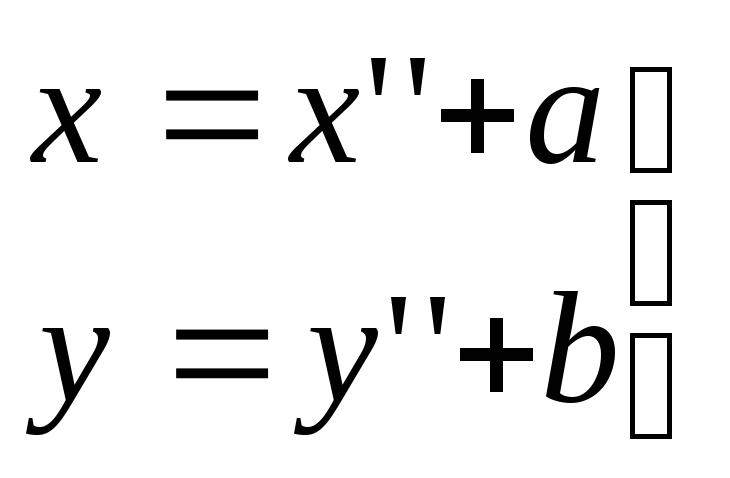(1)

П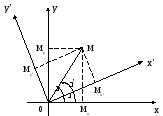оворот координатных осей

Пусть ,

.

,

.

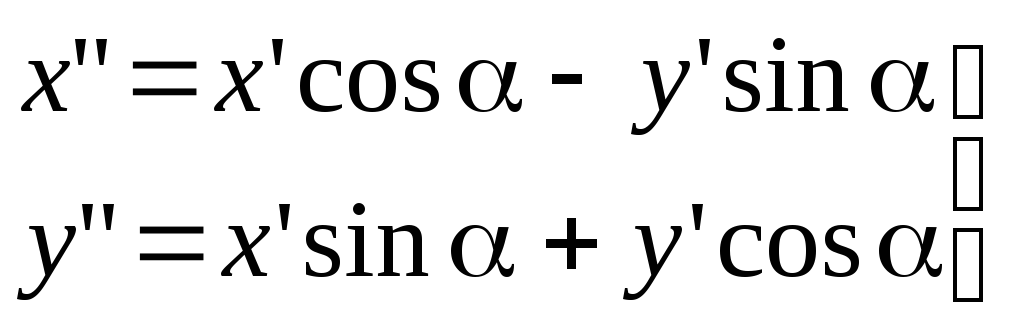(2)

Формулы (1) и (2) задают старые координаты точки через ее координаты в новой системе.

Рассмотрим приведение общего уравнения линии второго порядка к каноническому виду на примере.

Пусть дано общее уравнение второго порядка:

. (3)

Произведем параллельный перенос координатных осей в точку по формулам (1):.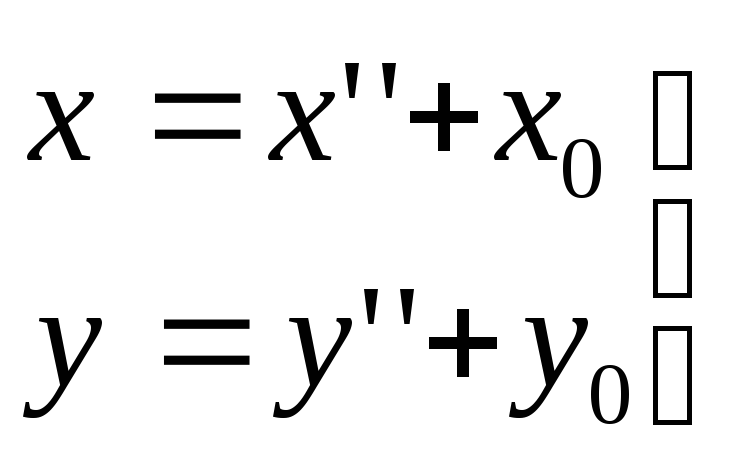

(3’)

Чтобы избавиться от членов первого порядка, приравняем коэффициенты при них к нулю:

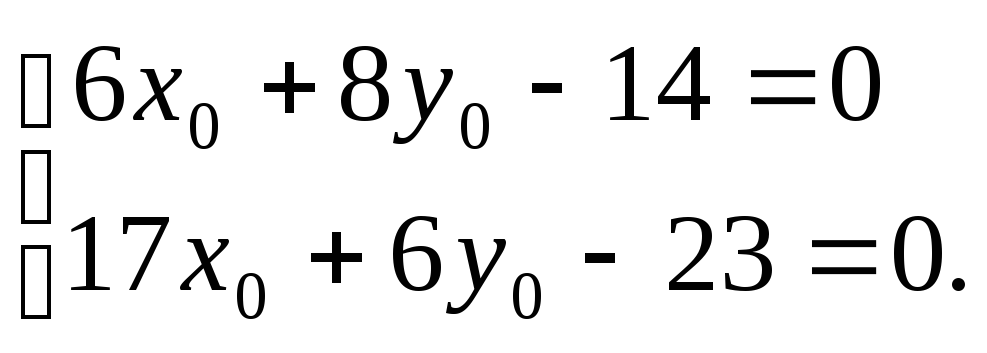
Решив систему, найдем координаты точки S, нового начала координат:S. Подставим эти координаты в уравнение (3’). В новых координатах уравнение примет вид:

(4)

Геометрический смысл преобразования – перенести начало координат в центр кривой.

Осталось повернуть оси, чтобы они совпали с осями симметрии кривой. Воспользуемся формулами поворота координатных осей (2).

(5)

Подбираем угол так, чтобы коэффициент при произведениистал равен нулю, т. е. решаем уравнение

.

,

.

Определяем и подставляем в (5):

.

Приводим уравнение к каноническому виду, разделив все коэффициенты на 20:

. (6)

Уравнение (6) – это каноническое уравнение эллипса с полуосями 2 (по оси О) и 1(по оси О).

Эллипс

О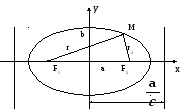пределение.Эллипс– это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскостииесть постоянная величина. Точкииназываются фокусами.

и - фокальные радиусы точки.

, ,

следовательно ,

.

Вывод уравнения эллипса

Дано: эллипс с фокусами и,– большая полуось,– половина расстояния между фокусами.

Возьмем за ось абсцисс прямую , а точкупоместим на середине отрезка. Пусть– произвольная точка плоскости. Пусть,.

По определению эллипса точка принадлежит эллипсу тогда и только тогда, когда

. (7)

Координаты фокусов равны соответственно ,, следовательно

, .

Подставим ив (7):

+=. (8)

(8) – уравнение эллипса в заданной системе координат. Преобразуем его к виду =и возведем в квадрат обе части уравнения:

.

;

;

; возведем в квадрат еще раз:

;

;

.

Обозначим , получим.

После приведения к каноническому виду уравнение эллипса запишется так:

. (9)

Эллипс, определяемый уравнением , симметричен относительнои.- центр эллипса,и- большая и малая полуоси эллипса.

При получаем- уравнение окружности.

Определение.Эксцентриситетэллипса – отношение расстояния между фокусами к длине его большей оси:. (10)

Так как , следовательно< 1.

, следовательно, .

Определение.Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянииот него, называетсядиректрисамиэллипса.

Их уравнения: и. Так как, следовательно,.