1.3. Запись приближенных значений величин. Верные знаки

Приближенные значения величин обычно записывают в виде десятичных дробей с конечным числом цифр.

Значащими цифрами в записи десятичной дроби называются все цифры, начиная с первой ненулевой слева. Например, в дроби 0,00102030004 значащими цифрами (подчеркнуты) являются все цифры, начиная с третьей после запятой.

Цифра в записи приближенного значения числовой величиныx называется верной в широком (строгом) смысле слова, если абсолютная погрешность приближенного значения не превышает единицы (половины единицы) разряда, в котором стоит эта цифра.

Все цифры верные в строгом смысле слова, очевидно, будут верными и в широком смысле. Рассмотрим несколько примеров.

Пример 1

Пусть ,= 0,000007899.Требуется найти верные цифры в записив широком и строгом смысле слова и подчеркнуть их одинарной и двойной линией соответственно. Проверяя для каждой цифры в записитребование, сформулированное в определении верных цифр, получим, что цифры 0, 1, 2, 3 и 4 будут верными в широком и строгом смысле слова одновременно. Цифра 5 будет верной в широком смысле слова, но не будет верной в строгом смысле слова:.

Отметим, что в разрядах, в которых в записи стоят незначащие нули, в записи стоят верные цифры в широком смысле слова.

Пример 2

Пусть теперь ,=0,000007899. Требуется найти верные цифры в записив широком и строгом смысле слова.

Абсолютная погрешность нам неизвестна, а известна лишь ее оценка . Если оценка абсолютной погрешностиприближенного значения не превышает единицы (половины единицы) разряда, в котором стоит цифра (в записи ), то эта цифра, очевидно, также будет верной в широком (строгом) смысле слова . Проверяя для каждой цифры в записи это требование, получим часть верных цифр: . Но, поскольку мы проверяем заведомо более жесткое требование, чемэто, среди неподчеркнутых цифр также могут оказаться верные, если погрешность окажется намного меньше своей оценки.

Отметим, что в тех разрядах, в которых в записи стоят незначащие нули, в записистоят верные цифры в широком смысле слова.

Пример 3

Пусть, =0,123456789, =0,123457899. В записи точного и приближенного значений подчеркнуты совпадающие цифры. Непосредственная проверка для каждой цифры в записи требования, сформулированного в определении верных цифр, показывает, что все подчеркнутые (совпадающие) цифры являются верными в широком смысле слова, а неподчеркнутые – неверными.

Но такое совпадение верных цифр (в широком смысле слова) в записи с соответствующими цифрами в записииногда нарушается. Это связано с тем, что некоторые вещественные числа могут записываться в десятичной системе двумя различными способами, например 1=1,0000...=0,9999… .

Пример 4

Пусть =1,0000…,=0,9999. В записи точного и приближенного значений нет ни одной совпадающей цифры. Непосредственная проверка для каждой цифры в записитребования, сформулированного в определении верных цифр, показывает, что цифры в записиявляются верными в широком смысле слова. В то же время если записатьдругим способом=0,9999…, то все верные цифры в записибудут совпадать с соответствующими цифрами в записи точного значения.

Рассмотренные примеры позволяют сформулировать некоторые свойства верных цифр.

Свойства верных цифр:

1. В тех десятичных разрядах, где в записи (или) стоят незначащие нули, в записидолжны стоять верные цифры в широком смысле слова (докажите это самостоятельно).

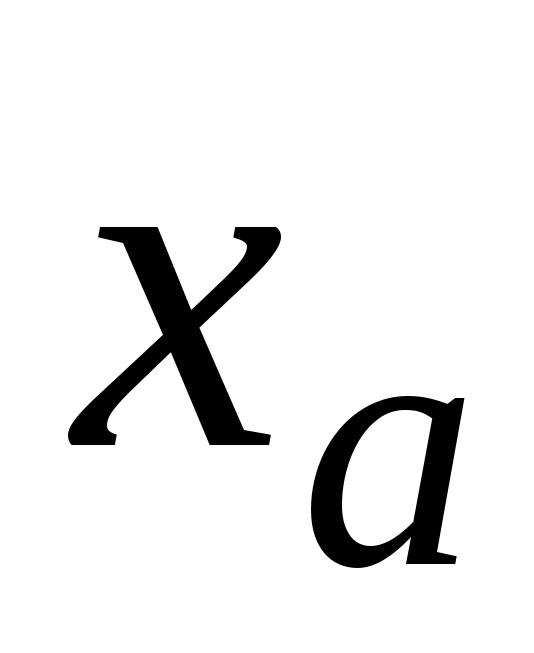2. Верные цифры в записи приближенного значения всегда совпадают с соответствующими цифрами в записи точного значения, если выбрать необходимую форму его записи в виде десятичной дроби

Установим теперь связь между величинами абсолютной и относительной погрешностей приближенного значения и количеством верных цифр в его записи. Пусть абсолютная погрешность приближенного значения равна. Определим количество верных цифр в широком смысле слова в записипосле запятой. Запишемв общем виде, указывая только разряды и не указывая конкретных цифр, и подчеркнем разряды, в которых будут располагаться верные цифры в широком смысле слова:

.

Итак, если абсолютная погрешность приближенного значения равна , то после десятичной запятой в записи будетn верных знаков.

Пусть теперь относительная погрешность приближенного значения равна. Установим общее количество верных знаков в записи. Для этого представимв показательной форме:. Здесь– вещественное число, называемое мантиссой, ар – целое число, называемое порядком . А для того, чтобы такое представление дроби было однозначным потребуем, чтобы

. (1.3.1)

Точное значение величины также запишем в показательной форме, причем с тем же порядкомp: . Для мантиссы точного значенияне будет выполняться условие (1.3.1). Значенияиестественно считать точным и приближенным значениями мантиссы величиныx. Тогда ипредставляют собой абсолютную и относительную погрешности приближенного значения мантиссы. Соответствующие цифры в записиидолжны совпадать попарно.Поэтому и количество верных цифр в записи ибудет одинаковым. Далее определяем количество верных цифр в записи. Запишем относительную погрешность

.

Отсюда

,

и, согласно формуле (1.3.1), для абсолютной погрешности получается оценка

(1.3.2)

Запишем в общем виде

.

Из формулы (1.3.1) следует, что первая цифра после десятичной запятой в записи должна быть отлична от нуля. Поэтому все цифры в записипосле запятой являются значащими. Из формулы (1.3.2) следует, что в записи мантиссы должно быть не меньшеn и не больше (n+1) верной цифры после десятичной запятой, причем все они являются значащими. Итак, в мантиссе имеется или n или (n+1) верная значащая цифра. Поэтому общее количество верных значащих цифр в записи также будет равно либоn, либо (n+1).

Таким образом, мы показали, что если относительная погрешность приближенного значения равна , то общее количество верных значащих цифр в записи равно либо n, либо (n+1).