Погрешности элементарных машинных операций

При реализации численных методов решения прикладных задач на ЭВМ данные обычно представляются в форме с плавающей запятой. Это означает, что если для реализации численного метода используется, например, среда программирования Pascal или Delphi, то при описании числовых данных для них выбираются вещественные типы, такие как single, real или extended. Рассмотрим, как оцениваются абсолютная и относительная погрешности результатов элементарных арифметических операций, выполненных на компьютере с данными в формате с плавающей запятой.

Пусть выполняется операция сложения двух чисели, записанных в память компьютера в формате с плавающей запятой. Компьютер производит сложение значенийx и y и записывает его результат в память. Сложение производится с помощью запасных разрядов, а затем результат сложения округляется. Операция сложения этих чисел производится практически точно, а окончательный результат сложения, записывается в память компьютера в виде . Поэтому единственный источник погрешности результатаz_a – округление при записи z в память компьютера. Согласно (1.15.10), получим

.

Отсюда

, (1.15.11)

. (1.15.12)

Дословно повторив эти рассуждения, можно доказать формулы (1.15.11), (1.15.12) для результатов остальных арифметических операций (вычитания, умножения и деления).

Операции машинной арифметики над данными представлениями в форме с плавающей запятой обладают некоторыми специфическими свойствами, которыми не обладают арифметические операции над вещественными числами.

Приведем два из них без доказательства.

1. Погрешность суммы нескольких положительных чисел (больше двух), записанных в форме с плавающей запятой, зависит от порядка суммирования этих чисел и принимает наименьшее значение, если числа суммируются в порядке возрастания.

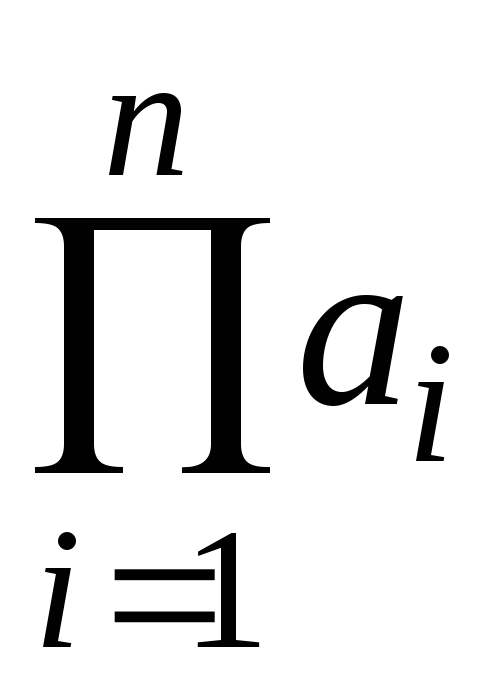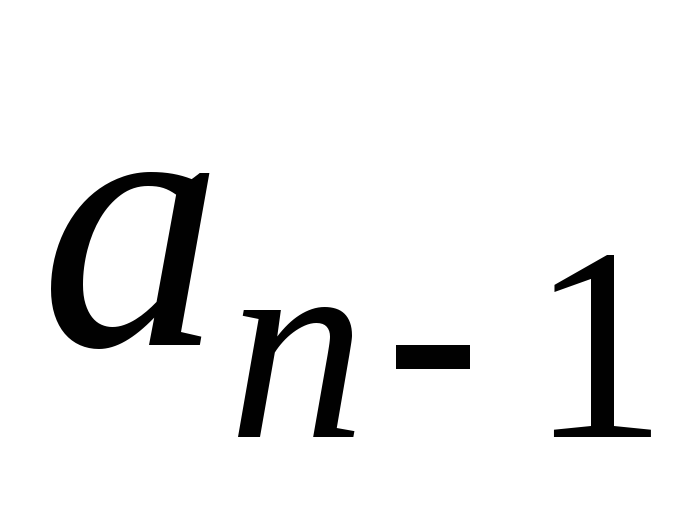2. Погрешность произведения чиселтаких, что, зависит от порядка умножения. Чтобы уменьшить по возможности эту погрешность необходимо производить умножение по схеме: умножатьпоследовательно на,, … до тех пор, пока модуль накапливаемого произведения не станет больше 1, затем это частичное произведение умножается на,, … до тех пор, пока модуль накапливаемого произведения не станет меньше 1, и так далее до исчерпывания всех сомножителей.

Итак, мы выяснили природу погрешностей, возникающих при вычислениях с помощью компьютера. Они связаны с ограниченностью используемой для записи чисел в память компьютера разрядной сетки и неизбежными округлениями практически всех числовых данных.

Общая тенденция роста вычислительной погрешности

Процесс вычисления окончательного численного результата в конечном счете представляет собой более или менее длинную последовательность элементарных арифметических операций, вычисляемых обычно на компьютере. Погрешности могут возникать на этапе ввода исходных числовых данных, и в дальнейшем каждая операция с данными в процессе вычислений вносит свою лепту в вычислительную погрешность окончательных численных результатов. Оценить эту погрешность часто бывает очень сложно, поскольку количество таких операций может быть очень велико. По этой причине зачастую весьма проблематично использовать для этих целей оценки погрешностей, приведенные в параграфах 1.5–1.8. Даже в тех случаях, когда это удается, оценки погрешности часто оказываются сильно завышенными, то есть реальная вычислительная погрешность оказывается значительно меньше получаемых оценок. Это связано с тем, что погрешности могут компенсироваться. Покажем это на следующем примере.

Пример 1

Пусть , а,,.

Точное значение суммы и приближенноесовпадают, и. В то же время,и формула 1.5.1 дает нам значение оценки погрешности, тогда как на самом деле погрешность.

Аналогичные примеры компенсации вычислительных погрешности легко построить и для других арифметических операций. Сделайте это самостоятельно.

С другой стороны, вычислительная погрешность имеет общую тенденцию к накоплению, то есть с ростом количества операций она растет.

Пример 2

Пусть ,а также заданы приближенные значения членов суммы , имеющих одинаковые оценки абсолютных погрешностей–const. Значение мало, аn велико. Пусть вычисляется приближенное значение . Тогда, согласно формуле 1.5.1, оценка абсолютной погрешности этого приближенного численного результата равна

.

Здесь  количество операций сложения.

Этот пример показывает, что оценка абсолютной погрешности N операций сложения (или вычитания) при больших значениях N прямо пропорциональна количеству операций N.

Аналогично можно показать, что оценка относительной погрешности результата N операций умножения и деления при больших значениях N прямо пропорциональна количеству операций N.

Рассуждая на эвристическом уровне строгости, можно предположить, что в большинстве случаев аналогичная картина наблюдается и для погрешностей, и для более сложных цепочек операций, в которых присутствуют все четыре арифметические операции. Иными словами, можно предположить, что в большинстве случаев абсолютная и относительная погрешности результата цепочки из N арифметических операций при больших значениях N прямо пропорциональна количеству операций N. Но, оказывается, что это не так. Реальная погрешность окончательного результата в большинстве случаев растет медленнее, очевидно, вследствие компенсации погрешностей. Математическое ожидание абсолютной погрешности результата в условиях примера 2 при достаточно большом значении n прямо пропорционально . В частности, приn>10 используют правило Чеботарева

.

Поэтому можно ожидать, что во многих случаях абсолютная и относительная погрешность результата цепочки из N арифметических операций при больших значениях N прямо пропорциональна . Но это всего лишьстатистическая тенденция, она может нарушаться в тех или иных конкретных случаях. Известны примеры, когда относительная или абсолютная погрешности результатов арифметических операций или их коротких цепочек очень резко увеличивается по сравнению с погрешностями аргументов. Наличие даже одного такого фрагмента в общей цепочке операций может катастрофически увеличить вычислительную погрешность окончательного результата.