1.13. Устойчивость и корректность постановки прикладной математической задачи

Для того чтобы решить прикладную задачу с использованием приближенных численных методов, необходимо быть уверенным, что она имеет единственное решение z для каждого допустимого набора исходных данных u. Но и этого часто недостаточно. Постановка прикладной математической задачи подразумевает не только выделение исходных данных, результатов, промежуточных величин и установление математических отношений между ними, но и исследование существования и единственности решения задачи z для каждого допустимого набора исходных данных и свойств зависимости z от u. Поэтому поставить задачу нередко бывает сложнее, чем получить ее численное решение.

В начале ХХ века Ж.Адамар ввел понятие корректно поставленной прикладной математической задачи и долгое время считали, что каждая прикладная математическая задача должна быть корректно поставлена. Попытки решения некорректно поставленных задач численными методами обычно бывали безуспешными. В то же время накопилось большое количество некорректно поставленных задач, имеющих большое практическое значение. В середине ХХ века А.Н.Тихоновым были созданы специальные численные методы, получившие название методов регуляризации, позволяющие решать некорректно поставленные задачи.

Рассмотрим более подробно основные понятия, связанные с постановками прикладных математических задач. Пусть имеется некоторая прикладная математическая задача, u и z – переменные, значениями которых являются наборы исходных данных и результатов, U и Z – метрические пространства с метриками и, которым принадлежат значения переменныхu и z. Эта прикладная задача называется корректно поставленной на паре метрических пространств (U,Z), если выполняются три условия:

1. Для любого uU существует хотя бы одно решение прикладной математической задачи zZ (существование решения прикладной задачи).

2. Не может существовать два разных решения прикладной задачи z₁ и z₂ (z₁≠z₂) при одних и тех же исходных данных u (единственность решения прикладной задачи).

3. Для любого найдетсятакое, что для любых наборов исходных данныхu₁, u₂ U , удовлетворяющих неравенству _u(u₁, u₂) < , выполняется неравенство_z(z₁, z₂ ) <. Здесьz₁ и z₂ – решения прикладной задачи, соответствующие исходным данным u₁ и u₂ .

Если прикладная задача удовлетворяет условиям 1 и 2 , то для любого uU найдется единственный элемент zZ , представляющий собой решение прикладной математической задачи. Иными словами, существует функция , которая ставит в соответствие каждому элементу, единственное решение краевой задачи.

Требование 3 означает непрерывность этой функции в пространстве U.

Прикладная задача, удовлетворяющая требованию 3, называется устойчивой на паре пространств (U, Z).

Если прикладная задача не удовлетворяет хотя бы одному из условий 1–3, то ее называют некорректно поставленной на паре пространств (U, Z).

Пример 1

Рассматривается задача дифференцирования функции одной переменной на заданном числовом сегменте . Здесьa и b –заданные постоянные (). Требуется ввести величины, значениями которых являются наборы исходных данных и результатовu и z, а также метрические пространства U и Z, элементами которых являются значения этих величин. Требуется также установить, является ли эта задача корректно поставленной на паре выбранных пространств (U,Z).

Исходными данными задачи являются концы сегмента, а также функция одной переменной, производную которой необходимо найти. Результат – производная этой функции. Обозначим функцию одной переменной, производную которой необходимо найти. Теперь введем переменнуюu, значениями которой являются векторы с тремя координатами , и переменнуюz, значениями которой являются векторы с одной координатой . Таким образом,

, (1.13.1)

. (1.13.2)

Выделим множество допустимых исходных данных U. В него, очевидно, целесообразно включить только такие наборы исходных данных, для которых наша задача имеет решения. Поэтому функция , входящая в допустимый набор, должна быть дифференцируема на отрезке. С другой стороны, нам необходимо ввести метрику на множествахU и Z. Предвидя это, удобно сузить множество допустимых наборов исходных данных. Будем относить к допустимым только такие наборы , для которых функция, входящая в набор, должна быть непрерывно дифференцируема на отрезке .Так мы введем множество U. В этом случае наша задача будет иметь единственное решение для любого допустимого набора исходных данных, причем функция, входящая в набор результатов, должна быть непрерывна на отрезке. Поэтомув качестве множества Z мы выберем множество наборов результатов ,для которых функция , входящая в набор, должна быть непрерывной на отрезке .

Введем на множестве Z метрику , совпадающую с известной метрикой, часто вводимой на множестве непрерывных функций:

, (1.13.3)

где ,.

Поскольку всякая дифференцируемая функция является непрерывной, введем метрику на множестве допустимых исходных данныхU аналогично:

, (1.13.4)

где ,. Но существует и другой способ введения метрики на:

. (1.13.5)

Докажите самостоятельно, что функция (1.13.5) удовлетворяет всем аксиомам метрики из параграфа 1.10. Отметим, что последняя метрика практически непригодна для использования, поскольку для ее вычисления требуется знать не только исходные данные, но и решение задачи.

Введем метрику (1.13.3) на множестве Z. В результате оно превратится в метрическое пространство, которое также обозначим Z. Метрические пространства, в которые превращается множество U, если на нем ввести метрики по формулам (1.13.4) и (1.13.5), обозначим и, соответственно.

Исследуем корректность постановки задачи дифференцирования на паре пространств (U₂,Z). Существование и единственность решения задачи для любого допустимого набора исходных данных не вызывает сомнений. Докажем устойчивость нашей задачи на паре пространств (U₂,Z). Зададим произвольное положительное число и выберем. Зададим произвольные допустимые наборы исходных данных,, удовлетворяющие неравенству. Тогда, очевидно, будет выполняться неравенство, что и требовалось доказать. Таким образом,задача дифференцирования является корректно поставленной на паре пространств (U₂,Z).

Исследуем корректность постановки задачи дифференцирования на паре пространств (U₁,Z). Существование и единственность решения задачи для любого допустимого набора исходных данных не вызывает сомнений. Докажем неустойчивость нашей задачи на паре пространств (U₁,Z). Для этого необходимо показать, что найдется число такое, что для любого числасуществуют допустимые наборы исходных данных,, удовлетворяющие неравенству, для которых выполняется неравенство. Покажем это. Положими зададим произвольное. Выберем произвольный допустимый набор исходных данных, а второй допустимый набор выберем следующим образом:. Здесь– положительное число, большееи такое, что. Тогдаи в то же время. Что и требовалось показать.

Таким образом, задача дифференцирования является некорректно поставленной на паре пространств (U₁,Z).

Замечание 1. Выбор метрики по формуле (1.13.5) делает задачу дифференцирования корректной, но использование этой метрики на практике весьма проблематично, поскольку для её вычисления требуется знать решение задачи и.

Пример 2

Рассматривается задача интегрирования (по Риману) функции одной переменной на заданном отрезке . Здесьa и b –заданные постоянные (). Требуется ввести величины исходных данных и результатовu и z, а также метрические пространства U и Z, элементами которых являются значения этих величин, установить является ли эта задача корректно поставленной на паре выбранных пространств (U,Z).

Обозначим – подынтегральную функцию, точное значения интеграла Римана . Исходными данными задачи являются концы промежутка интегрирования, а также подынтегральная функция. Результат – точное значение интеграла. Теперь введем переменнуюu, значениями которой являются векторы с тремя координатами , и переменнуюz, значениями которой являются вектора с одной координатой . Таким образом,

, (1.13.6)

. (1.13.7)

Выделим множество допустимых наборов исходных данных U. В него, очевидно, целесообразно включить только такие наборы исходных данных, для которых наша задача имеет решения. Поэтому функция , входящая в допустимый набор, должна быть интегрируема на отрезке. Но мы потребуем, чтобыбыла непрерывна на отрезке. Тогда мы сможем использовать ту же метрику, что и в предыдущем примере. Поэтомубудем относить к допустимым только такие наборы , для которых функция, входящая в набор, должна быть непрерывна на отрезке .Так мы введем множество U. В этом случае наша задача будет иметь единственное решение для любого допустимого набора исходных данных. 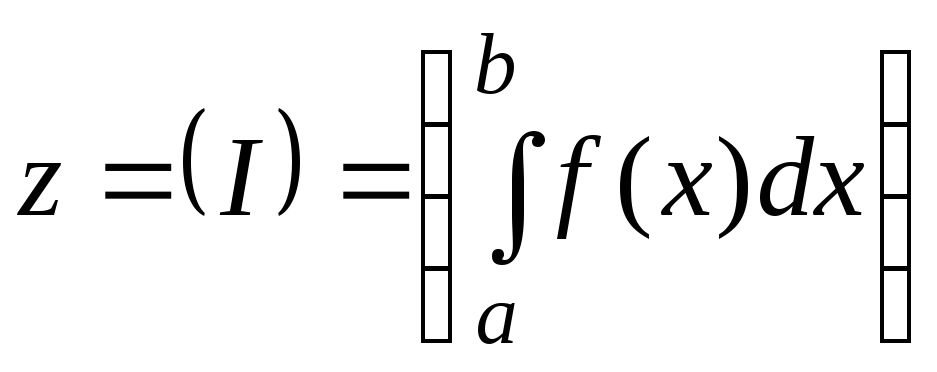Значение интеграла представляет собой вещественное число, поэтомув качестве множества Z мы выберем множество наборов результатов ,для которых величина I, входящая в набор, должна быть вещественным числом.

Введем на множестве U метрику , совпадающую с используемой в примере 1 метрикой:

, (1.13.8)

где , . А на множестве Z введем метрику, совпадающую с известной метрикой, обычно вводимой на множестве вещественных чисел:

, (1.13.9)

где ,. В результате этого множестваипревратятся в метрические пространства, которые обозначим такжеи. Исследуем корректность постановки нашей задачи интегрирования на паре пространств. Существование и единственность решения сформулированной задачи интегрирования для любого допустимого набора исходных данных, очевидно, выполняется. Докажем, что наблюдается и устойчивость решения задачи интегрирования.

Зададим произвольное число > и выберем число . Зададим произвольные допустимые наборы исходных данных , из , удовлетворяющие условию

<,

Тогда

.

Что и требовалось доказать. Таким образом, задача интегрирования на введенной паре пространств является устойчивой и корректно поставленной.

Пример 1 показал нам, что одна и та же прикладная задача может быть корректно поставленной на одной паре пространств и некорректно поставленной на другой. Более того, во многих случаях некорректно поставленную задачу можно превратить в корректно поставленную, если подобрать подходящее множество допустимых наборов исходных данных и метрику в нем.

Теорема. Пусть имеется произвольная прикладная математическая задача с единственным решением z для любого допустимого набора исходных данных u (существует функция ). Пусть U и Z – множества допустимых наборов исходных данных и результатов этой задачи, и на этих множествах введены метрики и.иZ – метрические пространства, в которые превращаются множества U и Z с введением этих метрик. Пусть на множестве U определена функция

, . (1.13.10)

Тогда функция представляет собой новую метрику на множествеU (получившееся новое метрическое пространство обозначим ), а описанная прикладная задача будет корректно поставлена на паре пространств .

Доказательство. Докажем, что функция удовлетворяет всем аксиомам метрики из параграфа 1.10.

В самом деле, при любых значения функциисуществуют и неотрицательны, поскольку значения каждой из метрикисуществуют и неотрицательны.

Если , то,,и, следовательно,.

Если , то обе метрики одновременно должны быть равны 0:и. Из первого равенства в силу первой аксиомы метрики, справедливой для, следует, чтои других вариантов нет.

Симметрия функции следует из симметрии метрики:

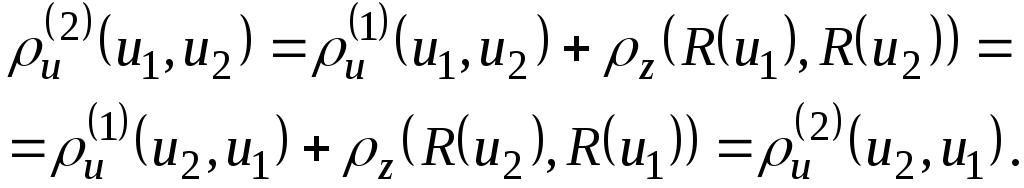
Выполнение неравенства треугольника для функции следует из того, что это неравенство выполняется для метрики:

Для завершения доказательства теоремы осталось показать устойчивость задачи на паре пространств . Зададим произвольное > и выберем . Зададим произвольные допустимые наборы исходных данных , из множества , удовлетворяющие условию

<,

Тогда

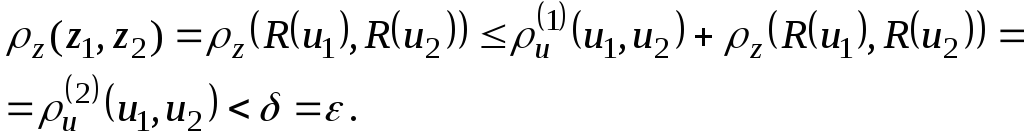
Что и требовалось доказать.

Теорема показывает, что не так сложно превратить некорректно поставленную прикладную задачу в корректную путем замены метрики метрикой, определяемой по формуле (1.13.10). Именно так и подбиралась вторая метрика из примера 1. Казалось бы, таким путем можно снять все проблемы, связанные с применением численных методов для решения некорректных задач. Но все не так просто. Дело в том, что метрика, введенная по формуле (1.13.10), непригодна для построения и исследования численных методов. Поэтому использование описанного способа получения корректных задач из некорректных обычно трансформирует трудности, возникающие при постановке задачи в неприятности, связанные с построением численных методов для ее решения. Убедиться в этом можно рассмотрев связь между постановкой задачи и численными методами ее решения. Об этом пойдет речь в следующем параграфе. Заметим только, что не существует общего метода для трансформации некорректно поставленных задач в корректные задачи, чтобы при этом сохранялись удобные для дальнейшего построения численных методов естественные метрики. Некорректные задачи приходится решать в их первоначальной формулировке и только с появлением методов регуляризации возникла возможность эффективного численного решения подобных задач.