
- •Глава 6. Тригонометрическая интерполяция. Наилучшее равномерное приближение
- •6.1. Тригонометрическая интерполяция. Дискретное преобразование Фурье Формулировка задачи интерполяции периодических функций тригонометрическими многочленами
- •Решение задачи интерполяции периодических функций тригонометрическими многочленами. Дискретное преобразование Фурье Решение задачи тригонометрической интерполяции
- •Дискретное преобразование Фурье
- •Оценка погрешности тригонометрической интерполяции
- •6.2. Наилучшее равномерное приближение
- •Контрольные вопросы и задания
Глава 6. Тригонометрическая интерполяция. Наилучшее равномерное приближение
В главе рассматриваются вопросы теории аппроксимации (тригонометрическая интерполяция и дискретное преобразование Фурье), имеющие практическое и теоретическое значение, а также вопросы наилучшего равномерного приближения.
6.1. Тригонометрическая интерполяция. Дискретное преобразование Фурье Формулировка задачи интерполяции периодических функций тригонометрическими многочленами
Рассматривается
задача интерполяции периодической
функции
![]() ,
имеющей некоторый положительный периодL.
Тогда для любого x
из области определения этой функции
должно выполняться равенство
,
имеющей некоторый положительный периодL.
Тогда для любого x
из области определения этой функции
должно выполняться равенство
![]() .
(6.1.1)
.
(6.1.1)
Будем считать, что известными являются значения этой функции в узлах равномерной сетки точек (узлах интерполяции)
![]() ,
,
![]() (6.1.2)
(6.1.2)
Обозначим
значения функции
![]() в узлах сетки
в узлах сетки
![]() ,
,
![]() (6.1.3)
(6.1.3)
И
Рис. 6.1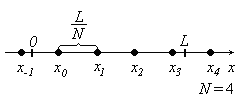
![]() и множества узлов интерполяции значения
функции
и множества узлов интерполяции значения
функции![]() будут также повторяться с периодомN
будут также повторяться с периодомN
![]() ,
,![]() (6.1.4)
(6.1.4)
В качестве интерполирующей функции выберем также периодическую функцию – тригонометрический многочлен n-го порядка, который будем записывать в виде
![]() ,(6.1.5)
,(6.1.5)
где
![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]()
произвольные вещественные постоянные
коэффициенты. При любых целых
неотрицательных значениях n
и при любых вещественных значениях
произвольные вещественные постоянные
коэффициенты. При любых целых
неотрицательных значениях n
и при любых вещественных значениях
![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() тригонометрический многочлен представляет
собой периодическую функцию с периодомL:
тригонометрический многочлен представляет
собой периодическую функцию с периодомL:
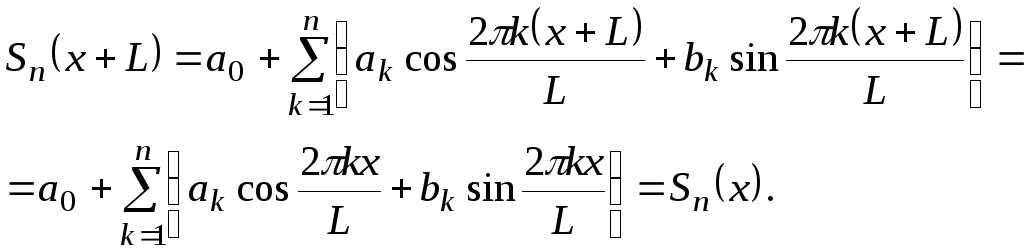 (6.1.6)
(6.1.6)
Отсюда
следует, что значения
![]() будут также повторяться с периодомN:
будут также повторяться с периодомN:
![]() ,
,
![]() (6.1.7)
(6.1.7)
Теперь
можно сформулировать задачу интерполяции
периодической функции
![]() тригонометрическими многочленами
тригонометрическими многочленами![]() .
.
Задача
тригонометрической интерполяции.
Требуется найти тригонометрической
многочлен n-го
порядка
![]() (подобрать коэффициенты
(подобрать коэффициенты![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() ),
удовлетворяющий условиям интерполяции:
),
удовлетворяющий условиям интерполяции:
![]() ,
,
![]() (6.1.8)
(6.1.8)
Обсудим
эту формулировку. Прежде всего, заметим,
что нет необходимости требовать
выполнения условий интерполяции (6.1.8)
при всех целых значениях m.
Так как значения
![]() и
и![]() повторяются с периодомN
достаточно потребовать выполнения
условий интерполяции (6.1.8) только на
периоде, то есть для любых N
целых значений величины m,
идущих
подряд, например при
повторяются с периодомN
достаточно потребовать выполнения
условий интерполяции (6.1.8) только на
периоде, то есть для любых N
целых значений величины m,
идущих
подряд, например при
![]() .
Учтя это замечание и подставив в формулу
(6.1.8) выражения для узлов интерполяции,
запишем условия интерполяции в виде
.
Учтя это замечание и подставив в формулу
(6.1.8) выражения для узлов интерполяции,
запишем условия интерполяции в виде
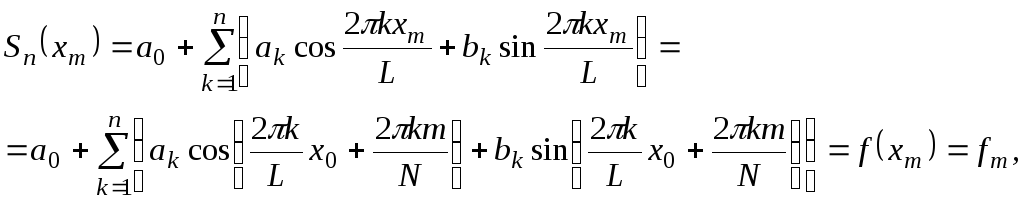 (6.1.9)
(6.1.9)
![]() .
.
Решение задачи интерполяции периодических функций тригонометрическими многочленами. Дискретное преобразование Фурье Решение задачи тригонометрической интерполяции
Условия
тригонометрической интерполяции (6.1.9)
представляют собой систему линейных
алгебраических уравнений с постоянными
коэффициентами. Количество уравнений
в этой системе равно N,
а количество неизвестных
![]() .
Для того чтобы эта система имела
единственное решение необходимо, чтобы
количество уравнений и неизвестных
совпадали:
.
Для того чтобы эта система имела
единственное решение необходимо, чтобы
количество уравнений и неизвестных
совпадали:
![]() .
(6.1.10)
.
(6.1.10)
Если число N является нечетным, то число n можно определить непосредственно из этой формулы
![]() .
(6.1.11)
.
(6.1.11)
Если число N является четным, то можно выбрать порядок тригонометрического многочлена по формуле
![]() ,
(6.1.12)
,
(6.1.12)
а
один из лишних последних коэффициентов
(![]() или
или![]() )
положить равным нулю и не включать
соответствующий член в сумму (6.1.5). Тогда
тригонометрический многочлен (6.1.5) будет
иметь
)
положить равным нулю и не включать
соответствующий член в сумму (6.1.5). Тогда
тригонометрический многочлен (6.1.5) будет
иметь![]() коэффициентов.
коэффициентов.
Далее мы будем решать задачу тригонометрической интерполяции для одного часто встречающегося частного случая. Пусть число N является четным, а
![]() .
(6.1.13)
.
(6.1.13)
В
этом случае узлы интерполяции
![]() ,
,![]() ,
…,
,
…,![]() будут располагаться симметрично
относительно середины отрезка
будут располагаться симметрично
относительно середины отрезка![]() (см. рис. 6.1). Выберемn
по формуле (6.1.12) и исключим из суммы
(6.1.5) член с коэффициентом
(см. рис. 6.1). Выберемn
по формуле (6.1.12) и исключим из суммы
(6.1.5) член с коэффициентом
![]() .
Тогда тригонометрический интерполяционный
многочлен примет вид
.
Тогда тригонометрический интерполяционный
многочлен примет вид
![]() .
(6.1.14)
.
(6.1.14)
Учитывая это представление для тригонометрического интерполяционного многочлена и условие (6.1.13), получим соответствующие условия тригонометрической интерполяции для рассматриваемого частного случая
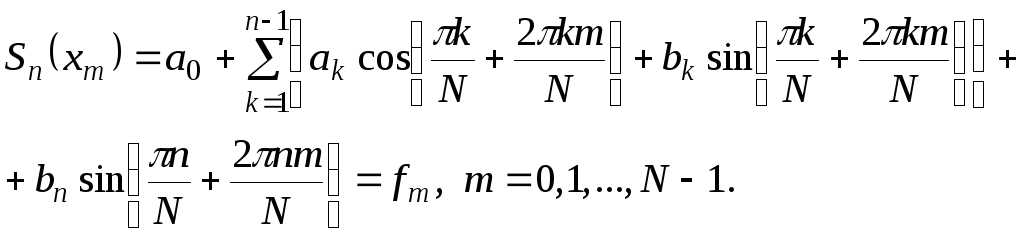 (6.1.15)
(6.1.15)
Количество
уравнений и неизвестных линейной системы
(6.1.15) совпадают при
![]() .
Решение системы (6.1.15) можно производить,
например, методом Гаусса, но в данном
случае можно получить и явные формулы
для вычисления искомых коэффициентов
тригонометрического интерполяционного
многочлена
.
Решение системы (6.1.15) можно производить,
например, методом Гаусса, но в данном
случае можно получить и явные формулы
для вычисления искомых коэффициентов
тригонометрического интерполяционного
многочлена![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() .
.
Введем
вектор f
с координатами
![]() ,
,![]() ,
…,
,
…,![]() .
.
Введем
векторы
![]()
![]() с координатами
с координатами![]() ,
,![]() ,
…,
,
…,![]() ,
вычисляемыми по формулам
,
вычисляемыми по формулам
![]() ,
,
![]() .
(6.1.16)
.
(6.1.16)
![]() ,
,
![]() ,
,![]() .
(6.1.17)
.
(6.1.17)
Введем
векторы
![]()
![]() с координатами
с координатами![]() ,
,![]() ,
…,
,
…,![]() ,
вычисляемыми по формулам
,
вычисляемыми по формулам
![]() ,
,
![]() ,
,![]() .
(6.1.18)
.
(6.1.18)
![]() ,
,
![]() .
(6.1.19)
.
(6.1.19)
В
процессе преобразований (6.1.19) учтено,
что
![]() .
.
С учетом введенных обозначений систему (6.1.15) можно записать в виде векторного равенства
![]() .
(6.1.20)
.
(6.1.20)
Рассмотрим
систему введенных векторов
![]() .
Общее количество векторов, входящих в
эту систему, равно 2n=N.
Если эта система векторов является
ортогональной, то она будет линейно
независимой и, следовательно, она будет
образовывать базис в линейном векторном
пространстве
.
Общее количество векторов, входящих в
эту систему, равно 2n=N.
Если эта система векторов является
ортогональной, то она будет линейно
независимой и, следовательно, она будет
образовывать базис в линейном векторном
пространстве
![]() .
Тогда формула (6.1.20) будет представлять
собой разложение вектораf
по этому
базису, а искомые коэффициенты
.
Тогда формула (6.1.20) будет представлять
собой разложение вектораf
по этому
базису, а искомые коэффициенты
![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]()
координаты вектора f
в этом базисе.
Найти эти координаты будет не сложно.
Поэтому мы в начале убедимся в
ортогональности нашей системы векторов.
координаты вектора f
в этом базисе.
Найти эти координаты будет не сложно.
Поэтому мы в начале убедимся в
ортогональности нашей системы векторов.
Напомним,
что скалярное произведение вектора f
с координатами
![]() ,
,![]() ,
…,
,
…,![]() и вектораg
с координатами
и вектораg
с координатами
![]() ,
,![]() ,
…,
,
…,![]() в линейном векторном пространстве
в линейном векторном пространстве![]() определяется
по формуле
определяется
по формуле
![]() ,
(6.1.21)
,
(6.1.21)
а условие ортогональности векторов f и g имеет вид
![]() .
(6.1.22)
.
(6.1.22)
Для
того чтобы система векторов
![]() была ортогональной, необходимо, чтобы
все ее векторы были попарно ортогональны:
была ортогональной, необходимо, чтобы
все ее векторы были попарно ортогональны:
![]() при
при
![]() ,
,![]() ,
(6.1.23)
,
(6.1.23)
![]() при
при
![]() ,
,![]() ,
(6.1.24)
,
(6.1.24)
![]() при
при
![]() ,
,![]() .
(6.1.25)
.
(6.1.25)
Поскольку
![]() и
и![]() вычисляются по формулам, отличающимся
от формул, задающих остальные векторы
вычисляются по формулам, отличающимся
от формул, задающих остальные векторы![]() и
и![]() ,
удобно будет выделить скалярные
произведения, содержащие эти вектора
в формулах (6.1.23)
(6.1.25):
,
удобно будет выделить скалярные
произведения, содержащие эти вектора
в формулах (6.1.23)
(6.1.25):
![]() ,
,
![]() ,
(6.1.26)
,
(6.1.26)
![]() при
при
![]() ,
,![]() ,
(6.1.27)
,
(6.1.27)
![]() при
при
![]() ,
,![]() ,
(6.1.28)
,
(6.1.28)
![]() ,
,
![]() ,
(6.1.29)
,
(6.1.29)
![]() при
при
![]() ,
,![]() .
(6.1.30)
.
(6.1.30)
Докажем равенство (6.1.26):
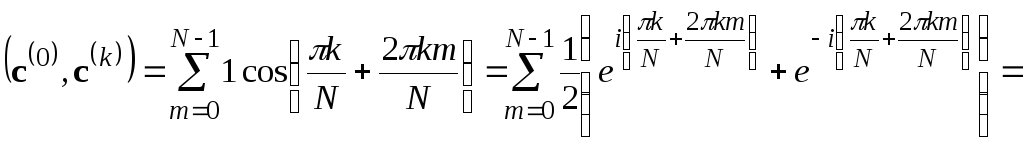
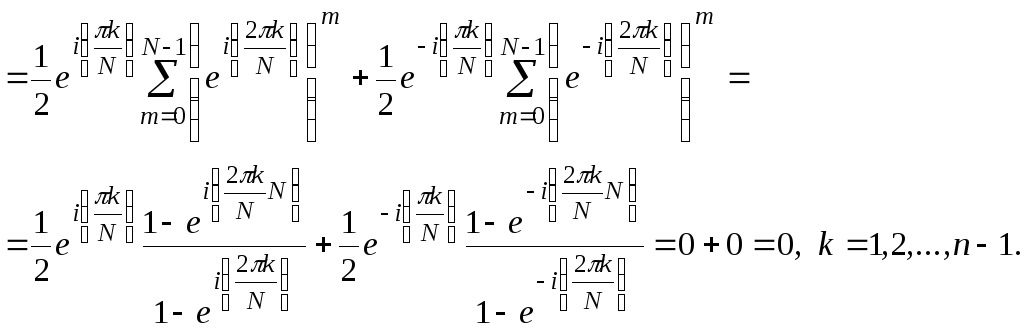 Здесь
i
–некий символ, такой что
Здесь
i
–некий символ, такой что
![]() .
В процессе преобразований использовалась
одна из формул Эйлера
.
В процессе преобразований использовалась
одна из формул Эйлера
![]() ,
,
![]() ,
,
свойства комплексной экспоненты, а также формула суммы геометрической прогрессии
![]() .
.
Равенство (6.1.26) доказано. Остальные условия ортогональности можно доказать аналогично.
Для
определения координат вектора f
в ортогональном
базисе
![]() умножим скалярно обе части равенства
(6.1.20) последовательно на все базисные
векторы:
умножим скалярно обе части равенства
(6.1.20) последовательно на все базисные
векторы:
![]() ,
,
![]() ,
,
…………………………………………….
![]() ,
(6.1.31)
,
(6.1.31)
![]() ,
,
…………………………………………….
![]() ,
,
![]() .
.
Учитывая
условия ортогональности (6.1.26)
(6.1.30), а также то, что
![]() ,
получим из системы (6.1.31)
,
получим из системы (6.1.31)
![]() ,
,
![]() ,
,
……………………
![]() ,
(6.1.32)
,
(6.1.32)
![]() ,
,
……………………
![]() ,
,
![]() .
.
Для определения неизвестных коэффициентов осталось найти квадраты модулей базисных векторов.
![]() ,
(6.1.33)
,
(6.1.33)
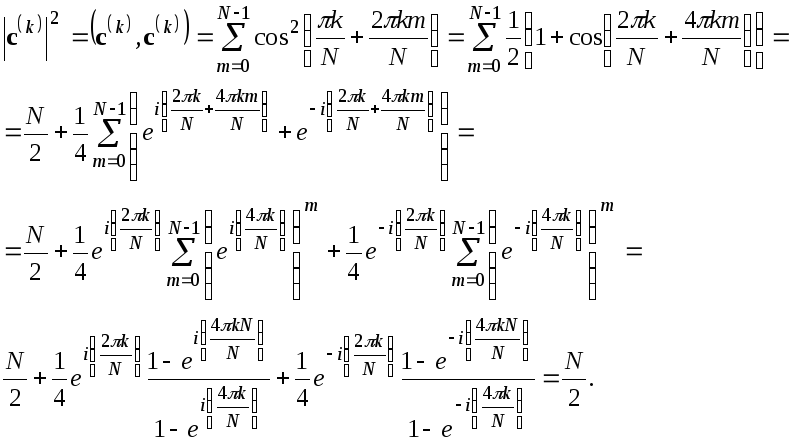
![]() .
В процессе преобразований использовалась
одна из формул Эйлера, свойства комплексной
экспоненты, а также формула суммы
геометрической прогрессии. Итак, мы
показали, что
.
В процессе преобразований использовалась
одна из формул Эйлера, свойства комплексной
экспоненты, а также формула суммы
геометрической прогрессии. Итак, мы
показали, что
![]() ,
,
![]() .
(6.1.34)
.
(6.1.34)
Аналогично можно доказать, что
![]() ,
,
![]() .
(6.1.35)
.
(6.1.35)
Значение последнего модуля находится легко:
![]() .
(6.1.36)
.
(6.1.36)
С помощью формул (6.1.32) (6.1.36) получим искомые коэффициенты тригонометрического интерполяционного многочлена
![]() ,
(6.1.37)
,
(6.1.37)
![]() ,
,
![]() ,
(6.1.38)
,
(6.1.38)
![]() ,
,
![]() ,
(6.1.39)
,
(6.1.39)
![]() .
(6.1.40)
.
(6.1.40)
Итак,
мы построили тригонометрический
интерполяционный многочлен для частного
случая расположения узлов интерполяции,
когда
![]() .
Получены тригонометрические
интерполяционные многочлены и для
других частных случаев, а также для
общего случая произвольной равномерной
сетки узлов.
.
Получены тригонометрические
интерполяционные многочлены и для
других частных случаев, а также для
общего случая произвольной равномерной
сетки узлов.
