
- •Глава 8. Численное интегрирование
- •8.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона – Котеса Постановка задачи приближенного интегрирования. Квадратурные формулы
- •Квадратурные формулы Ньютона – Котеса
- •Необобщенные формулы прямоугольников, трапеций, Симпсона
- •Обобщенные формулы прямоугольников, трапеций, Симпсона
- •Оценка погрешности и определение порядка точности для формулы трапеций
- •Оценка погрешности и определение порядка точности обобщенной формулы трапеций. Преобразуем разность между точным и приближенным значениями интеграла, вычисленным с помощью обобщенной формулы трапеций:
- •Оценки погрешности и порядки точности обобщенных квадратурных формул прямоугольников, трапеций и Симпсона
- •8.2. Квадратурные формулы Гаусса. Метод неопределенных коэффициентов Квадратурные формулы Гаусса
- •Метод неопределенных коэффициентов
- •8.3. Метод Монте-Карло
- •Первая схема метода Монте-Карло
- •Вторая схема метода Монте-Карло
- •8.4. Вычисление первообразных, несобственных и кратных интегралов
- •Вычисление первообразных
- •Вычисление несобственных интегралов
- •Вычисление кратных интегралов. Кубатурные формулы
- •8.5. Обусловленность квадратурных формул интерполяционного типа
- •Контрольные вопросы и задания
Глава 8. Численное интегрирование
Решение многих прикладных задач часто сводятся к задаче вычисления интеграла. Для аналитического вычисления интеграла необходимо установить первообразную подынтегральной функции. В некоторых частных случаях это удается сделать (все эти случаи представлены в задачниках по математическому анализу и справочниках), но в общем виде задача вычисления интеграла аналитического решения не допускает. Именно для таких случаев и создаются методы численного интегрирования, позволяющие получать приближенные значения интегралов с любой точностью.
8.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона – Котеса Постановка задачи приближенного интегрирования. Квадратурные формулы
Задача
приближенного вычисления определенного
интеграла
![]() ,
формулируется следующим образом. Для
заданного положительного числа
,
формулируется следующим образом. Для
заданного положительного числа![]() требуется найти приближенное значение
интегралаQ,
абсолютная погрешность которого не
превышает
требуется найти приближенное значение
интегралаQ,
абсолютная погрешность которого не
превышает
![]() :
:
![]() .
.
Один
из наиболее широко используемых способов
приближенного вычисления интегралов
связан с применением квадратурных
формул. Идея использования квадратурных
формул заложена в определении интеграла.
Напомним его. Для этого отрезок
![]() разобьем наn
отрезков точками
разобьем наn
отрезков точками
![]() .
На всех отрезках разбиения произвольным
образом выбираются точки
.
На всех отрезках разбиения произвольным
образом выбираются точки![]() и обозначим
и обозначим![]() ,
,![]() .
.
Согласно определению, интеграл Римана представляет собой предел интегральных сумм
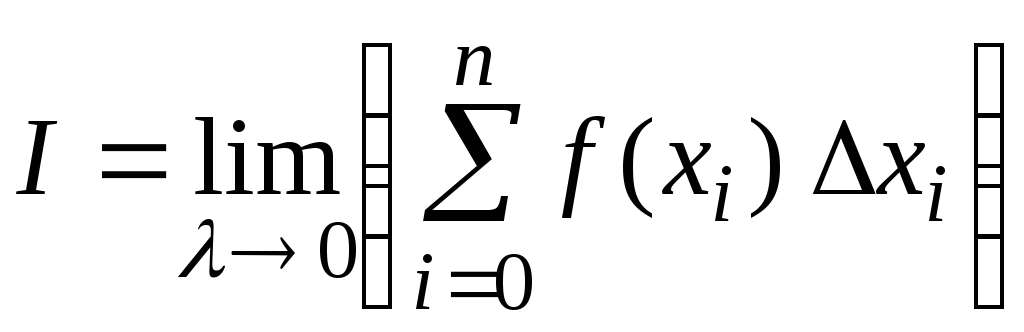 .
(8.1.1)
.
(8.1.1)
Отсюда следует, что интеграл I с любой точностью можно приблизить суммами вида
![]() ,
,
где
![]()
точки, принадлежащие отрезку
точки, принадлежащие отрезку
![]() ,
а
,
а![]()
некоторые постоянные числа. Таким
образом, получается приближенная формула
некоторые постоянные числа. Таким
образом, получается приближенная формула
![]() ,
(8.1.2)
,
(8.1.2)
которую
мы в дальнейшем будем называть квадратурной
формулой.
Точки
![]() будем называтьузлами,
а числа
будем называтьузлами,
а числа
![]()
коэффициентами
квадратурной формулы.
Разность
коэффициентами
квадратурной формулы.
Разность
![]() (8.1.3)
(8.1.3)
называется остаточным членом (остатком) квадратурной формулы. Последнюю формулу можно переписать в виде
![]() .
(8.1.4)
.
(8.1.4)
Для
решения задачи приближенного интегрирования
с помощью квадратурной формулы (8.1.2)
необходимо подобрать параметры
![]() так, чтобы абсолютная погрешность
вычисляемого приближенного значения
интеграла
так, чтобы абсолютная погрешность
вычисляемого приближенного значения
интеграла![]() не превышала
не превышала![]() ,
то есть
,
то есть
![]() .
(8.1.5)
.
(8.1.5)
Квадратурные формулы Ньютона – Котеса
Один
из наиболее распространенных способов
получения квадратурных формул основан
на использовании приближений
подынтегральной функции интерполяционными
многочленами. Подынтегральная функция
![]() приближенно заменяется интерполяционным
многочленом
приближенно заменяется интерполяционным
многочленом![]() ,
где
,
где![]()
узлы интерполяции, выбранные на отрезке
узлы интерполяции, выбранные на отрезке
![]() .
В качестве приближенного значения
интегралаQ
выбирается интеграл от интерполяционного
многочлена (в форме Лагранжа)
.
В качестве приближенного значения
интегралаQ
выбирается интеграл от интерполяционного
многочлена (в форме Лагранжа)
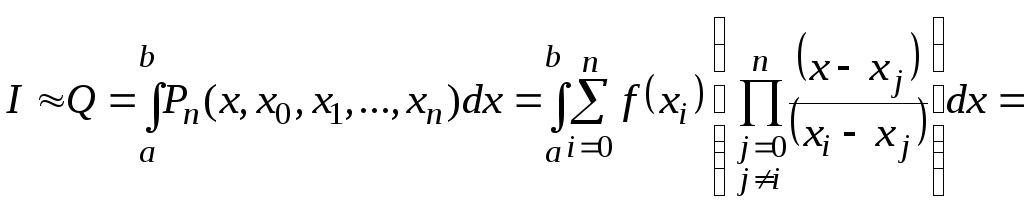
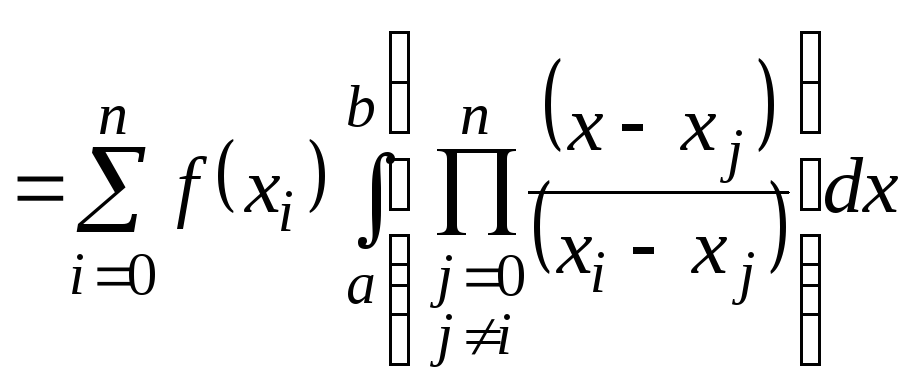 .
(8.1.6)
.
(8.1.6)
Если
обозначить
 ,
то формула (8.1.6) превратится в квадратурную
формулу. Квадратурные формулы,
интерполяционного типа, построенные
на основе равноотстоящих узлов, называютформулами
Ньютона – Котеса.
,
то формула (8.1.6) превратится в квадратурную
формулу. Квадратурные формулы,
интерполяционного типа, построенные
на основе равноотстоящих узлов, называютформулами
Ньютона – Котеса.
Далее
мы рассмотрим наиболее часто встречающиеся
квадратурные формулы Ньютона – Котеса,
которые получаются описанным способом,
при разных значениях n
и различном выборе узлов
![]() .
.
Необобщенные формулы прямоугольников, трапеций, Симпсона
Запишем
формулу (8.1.6) при
![]() ,
,![]() .
Тогда
.
Тогда![]() ,
,
![]() .
(8.1.7)
.
(8.1.7)
Формула (8.1.7) называется формулой левых прямоугольников.
Р
Рис. 8.1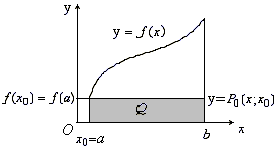
![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюOx.
Приближенное значение интеграла
Q
численно равно площади прямоугольника,
ограниченного сверху горизонтальной
прямой
,
а снизу – осьюOx.
Приближенное значение интеграла
Q
численно равно площади прямоугольника,
ограниченного сверху горизонтальной
прямой
![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюOx
(рис. 8.1.1).
,
а снизу – осьюOx
(рис. 8.1.1).
Запишем
теперь формулу (8.1.6) при
![]() ,
,![]() .
Тогда
.
Тогда![]() ,
,
![]() .
(8.1.8)
.
(8.1.8)
Ф
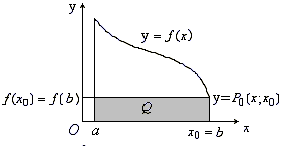 Рис.
8.2
Рис.
8.2![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюOx
(рис. 8.2).
,
а снизу – осьюOx
(рис. 8.2).
Запишем
формулу (8.1.6) при
![]() ,
,![]() .
.
Тогда
![]() ,
,
![]() .
(8.1.9)
.
(8.1.9)
Ф
Рис. 8.3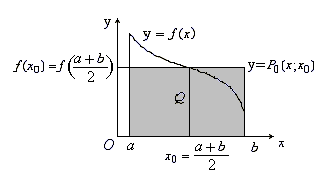
![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюx
(рис. 8.3).
,
а снизу – осьюx
(рис. 8.3).
Запишем
формулу (8.1.6) при
![]() ,
,![]() ,
,![]() .
Тогда
.
Тогда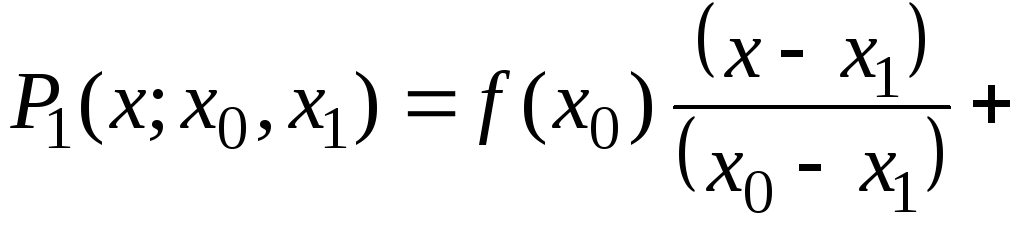
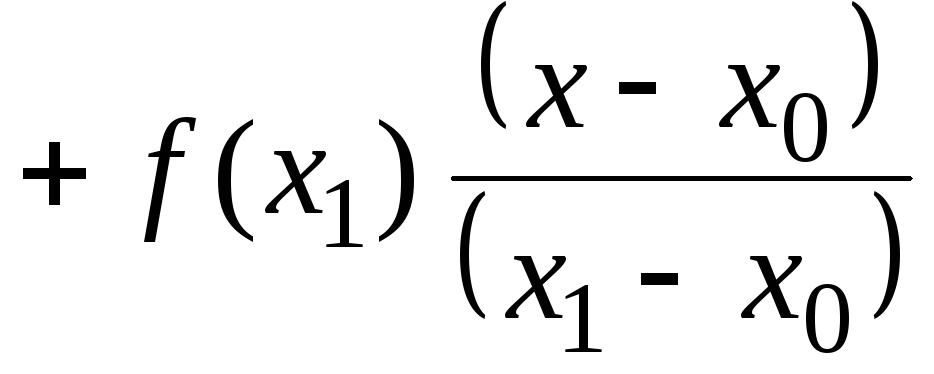 ,
,
![]()
![]()
![]() .
(8.1.10)
.
(8.1.10)
Ф
Рис. 8.4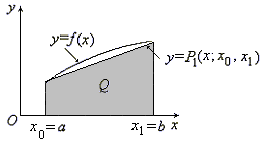
![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюx
(рис. 8.4).
,
а снизу – осьюx
(рис. 8.4).
Запишем
формулу (8.1.6) при
![]() ,
,![]() ,
,![]() ,
,![]() .
Тогда
.
Тогда
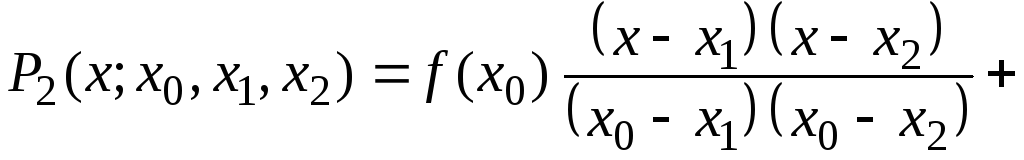
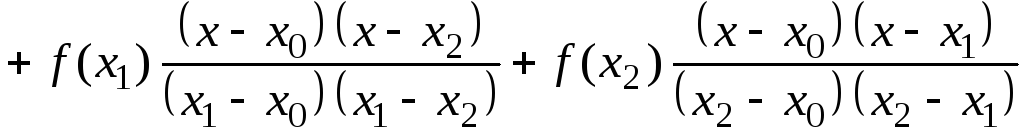 ,
,
![]()
![]()
![]() .
(8.1.11)
.
(8.1.11)
Ф
Рис. 8.5
Рассмотрим
геометрический смысл формулы Симпсона.
Приближенное значение интеграла Q
численно равно площади трапеции,
ограниченной сверху параболой
![]() ,
справа и слева
вертикальными прямыми
,
справа и слева
вертикальными прямыми
![]() и
и![]() ,
а снизу – осьюx
(рис. 8.5).
,
а снизу – осьюx
(рис. 8.5).
