225

Глава 4. Многочленная интерполяция

Глава 4. Многочленная интерполяция

Большая часть численных методов позволяет получать не точные, а приближенные решения математических задач. Поэтому очень важной в вычислительной математике является задача приближения (аппроксимации) различных математических объектов. Чаще всего приближаются (аппроксимируются) функции. А один из самых распространенных способов аппроксимации функций – интерполирование. Оно используется в тех случаях, когда основная информация о приближаемой функции дается в виде таблицы ее значений, а табличные значения имеют незначительные погрешности.

4.1.Интерполяционный многочлен Лагранжа Постановка задачи интерполирования

Пусть функция определена на заданном отрезке. Известны значения функциив отдельных точках() этого отрезка. Вычисление значений этой функции в других точках отрезкалибо очень трудоемко, либо вообще невозможно. В таких условиях обычно стараются получить приближение для функции, которым можно было бы воспользоваться для вычисления приближенных значений функции в других точках отрезкаили для других целей.Под приближением функции на отрезке понимается некоторая другая функция ,определенная на этом отрезке ,значения которой достаточно близки к соответствующим значениям функции .

При построении приближений для функций с известной таблицей значений используется несколько способов. Самый распространенный из них называется интерполяцией. При интерполяции от приближения требуется, чтобы оно имело ту же таблицу значений, что и приближаемая функция:

, . (4.1.1)

Это условие получило название условия интерполяции. Функция ,удовлетворяющая условиям интерполяции, называется интерполяционной, а точки  узлами интерполяции.

Чаще всего в качестве интерполяционных функций выбирают алгебраические многочлены, поскольку их значения проще всего вычисляются. В результате возникает следующая задача.

Задача многочленной интерполяции. Ищется алгебраический многочлен n-й степени , удовлетворяющий условиям интерполяции

. (4.1.2)

Алгебраический многочлен, удовлетворяющий условиям (4.1.2), называется интерполяционным многочленом. При записи интерполяционного многочлена будем использовать также более развернутое обозначение , в котором указываются узлы интерполяции в качествепараметров.

Геометрический смысл интерполяции состоит в том, что графики функции и интерполяционного многочленадолжны проходить через все табличные точки, (). На рис. 4.1 эти точки выделены. Именно это условие должно обеспечить близость графиков этих функций на отрезке, чтобы можно было использовать интерполяционный многочленв качестве приближения для функции. И

Рис. 4.1

нтуитивно понятно, что если табличных точекбудет много и они будут расположены густо, то графики функциии интерполяционного многочленабудут расположены близко друг к другу.

Обычно постановка любой прикладной математической задачи подразумевает исследование существования и единственности ее решения. Поэтому далее займемся этими вопросами в отношении задачи многочленной интерполяции.

Будем искать решение задачи интерполяции в виде

. (4.1.3)

Требуется определить набор постоянных () таким образом, чтобы алгебраический многочлен (4.1.3) удовлетворял условию интерполяции (4.1.2). Для этого подставим формулу (4.1.3) в формулу (4.1.2):

(4.1.4)

Система (4.1.4) представляет собой систему линейных алгебраических уравнений с постоянными коэффициентами относительно неизвестных постоянных . Определитель матрицы этой системы

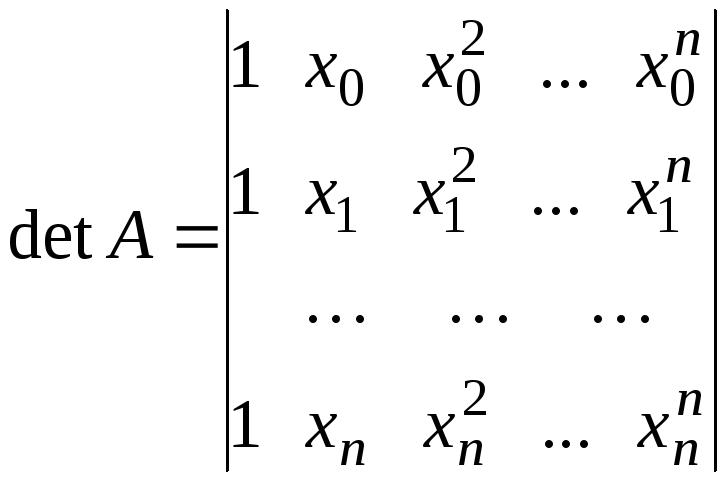
хорошо известен и получил название определителя Вандермонда. Доказано, что если все узлы интерполяции попарно различны, то определительВандермонда не равен нулю. Таким образом, система (4.1.4) должна иметь единственное решение, если все попарно различны. Обозначим это решение . Подставляя координаты этого вектора в формулу (4.1.3), получим интерполяционный многочлен в виде

. (4.1.5)

Таким образом, доказано существование и единственность интерполяционного многочлена, если все узлы интерполяции попарно различны. На этом постановку задачи многочленной интерполяции закончим. Фактически мы не только поставили эту задачу, но и получили метод ее решения, сведя задачу интерполяции к задаче решения линейной системы.