101

Глава 1. Теория погрешностей

Глава 1. Теория погрешностей

Одна из особенностей численных методов состоит в том, что результаты, получаемые с их помощью, в большинстве случаев являются не точными, а приближенными.

При вычислениях по заданным формулам нередко возникают ситуации, когда результат вычислений имеет погрешность, то есть он не совпадает с точным значением вычисляемой величины. Так случается, если аргументы формулы заданы не точно (если они, например, являются результатами измерений, округлений или приближенных вычислений) или значение искомой величины не выражается в виде десятичной дроби с достаточно маленьким числом цифр и его приходится округлять. Кроме того, решение очень многих задач невозможно найти точно. Даже числовые значения элементарных функций во многих случаях определяют с погрешностью (например, невозможно определить точные числовые значения функции или). Подобные погрешности не устранимы.Поэтому необходимо научиться работать с приближенными значениями величин и оценивать их точность. Этим мы и займемся в первой главе учебного пособия.

1.1.Абсолютная и относительная погрешности. Оценки погрешностей

Числовая величина представляет собой упорядоченную пару, первый элемент которой называется именем величины, а второй – ее значением. Значения числовых величин представляют собой числа, а в качестве имен используются буквы. Равенство означает либо констатацию факта, что значением числовой величины с именемx является число 1, либо, что числовой величине с именем x присваивается новое значение 1 взамен значения, которое она имела ранее. Величины, не изменяющие своего значения называют постоянными, а величины, изменяющие своё значение – переменными.

Любая числовая величина (только постоянная и переменная) может иметь только одно числовое значение до тех пор, пока ей не присвоили другое значение. Именно этозначение (которое присвоено величине в данный момент) будем называть точным значением величины. Точные значения числовых величин будем обозначать, приписывая к их именам снизу индекс e. Например, точное значение величины x обозначается .

Приближенным значением числовой величины называют любое число, которое выбирается вместо точного значения для каких-либо целей. Приближенные значения числовых величин будем обозначать, приписывая к их именам снизу индекс a. Например, приближенное значение величины x обозначается .

Приближенные значения вводятся в тех случаях, когда точное значение невозможно определить или записать в виде десятичной дроби с достаточно малым числом цифр. Точное значение одной величины может быть только одно, а приближенных – сколько угодно. Чем ближе приближенное значение к точному, тем выше его качество для нас. Но понятие "ближе" зависит от введенной меры близости. В теории погрешности используются две таких меры, называемых абсолютной и относительной погрешностью.

Абсолютной погрешностью приближенного значения числовой величиныx называется .

Относительной погрешностью приближенного значения числовой величиныx называется .

В одних случаях удобнее использовать первую меру близости между приближенным и точным значением, а в других – вторую.

Поскольку приближенное значение числовой величиныx вводится только в тех случаях, когда точное значение этой величины () неизвестно, абсолютную и относительную погрешностивычислить практически невозможно. Поэтому на практике обычно используются не сами погрешности, а их оценки. Введем понятия оценок погрешностей.

О точном значении числовой величины должна быть какая-то информация. Эта информация может быть преобразована и в конечном счете сведена к требованию, чтобы точное значение величины принадлежало некоторому числовому множеству, которое мыбудем называть множеством принадлежности точного значения числовой величины. Обозначать множества принадлежности числовых величин мы будем буквой Е, приписывая к ней в качестве индекса имя числовой величины. Например, множество принадлежности точного значения числовой величины x обозначается и для него должно быть справедливо отношение

. (1.1.1)

Если о точном значении величины x ничего не известно, то , а если, напротив, о нем имеется исчерпывающая информация, то это значит, что точное значениеможно найти и множествобудет состоять из одной точки.

Если множество принадлежности не ограничено, то есть оно не содержится в отрезке конечной длины, то, как бы мы ни выбирали приближенное значение, его погрешностьможет оказаться сколь угодно велика.

П

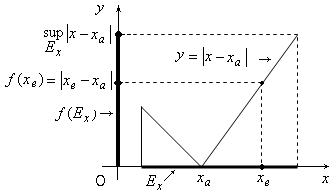Рис. 1.1

усть множество принадлежности точного значения числовой величиныx (множество ) ограничено. Рассмотрим функцию . Значение функции совпадает с абсолютной погрешностью (рис. 1.1). Таким образом, значение абсолютной погрешностипринадлежит множеству значений этой функции. Поскольку множествоограничено, рассматриваемая функция будет также ограничена на и будут существовать конечные верхние и нижние границы этой функции (границы ее множества значений) (рис. 1.1).

Оценкой абсолютной погрешности приближенного значения числовой величины x называется любая из верхних границ функции на множестве.

Оценок абсолютной погрешности приближенного значения существует бесчисленное множество. На рис. 1.1 – это все точки осиy, лежащие выше множества значений . Мы будем обозначать любую из оценок абсолютной погрешности как –. В соответствии с определением любая из оценок абсолютной погрешностидолжна быть не меньше самой абсолютной погрешности

(1.1.2)

Наилучшей из оценок абсолютной погрешности приближенного значения будет наименьшая из них, поскольку ее значение ближе всех других оценок к значению абсолютной погрешности (рис. 1.1). Эта оценка получила названиепредельной абсолютной погрешности. Таким образом, предельная абсолютная погрешность вычисляется по формуле

. (1.1.3)

Оценкой относительной погрешности приближенного значения числовой величины x называется любая из верхних границ функции на множестве.

Оценок относительной погрешности приближенного значения также существует бесчисленное множество, если множествоограничено. Мы будем обозначать любую из них. Любая из оценок относительной погрешностидолжна быть не меньше самой относительной погрешности

. (1.1.4)

Наилучшей из оценок относительной погрешности приближенного значения будет наименьшая из них. Эта оценка получила названиепредельной относительной погрешности. Таким образом, предельная относительная погрешность вычисляется по формуле

. (1.1.5)

Между множествами оценок абсолютной и относительной погрешности приближенного значения существует очевидное взаимно-однозначное соответствие:

или . (1.1.6)

Пример

Рис. 1.2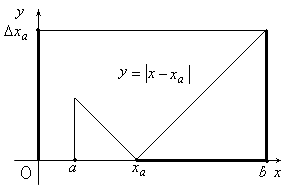

Множество принадлежности точного значения величиныx представляет собой заданный отрезок . Требуется подобрать приближенное значениетак, чтобы предельная абсолютная погрешность его была наименьшей.

Предельная абсолютная погрешность равна расстоянию от точкидо наиболее удаленного от этой точки конца(рис. 1.2):

.

Наименьшее значение это расстояние имеет тогда, когда приближенное значение величины совпадает с серединой отрезка :

. (1.1.7)

Предельная абсолютная погрешность выбранного по формуле (1.1.7) приближенного значения равна

. (1.1.8)