Метод неопределенных коэффициентов

Идея построения квадратурных формул, которые являются точными для алгебраических многочленов определенных степеней, используется и в методе неопределенных коэффициентов. Но, в отличие от изложенного метода теперь узлы квадратурной формулы задаются произвольно, а коэффициенты подбираются так, чтобы квадратурная формула была точна для произвольных многочленов как можно более высокой степени. В этом и заключается основная идея метода неопределенных коэффициентов.

Рассмотрим метод неопределенных коэффициентов на конкретном примере. Пусть требуется построить квадратурную формулу вида

. (8.2.13)

при . Коэффициенты квадратурной формулыбудем подбирать так, чтобы эта формула была точна для произвольного алгебраического многочлена наиболее высокой (насколько это возможно) степени.

Пусть подынтегральная функция представляет собой произвольный алгебраический многочлен степениm

. (8.2.14)

Потребуем, чтобы равенство (8.2.13) было точным при и при любых значениях величин:

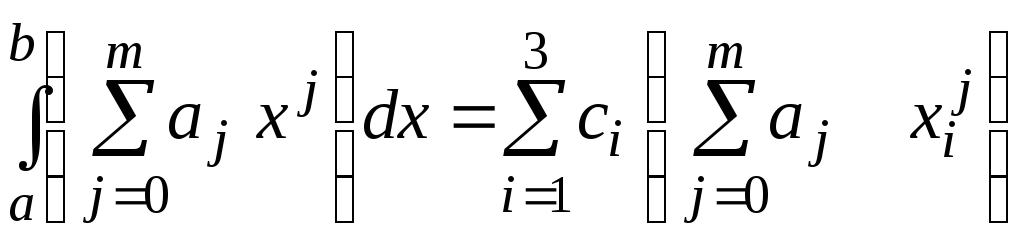. (8.2.15)

Найдем интеграл в левой части этого равенства и изменим порядок суммирования в правой части:

.

Вычислив подстановку в левой части этого равенства, получим

. (8.2.16)

Равенство (8.2.16) будет выполняться, если будут выполнены равенства

, . (8.2.17)

Итак, мы получили линейную систему уравнений с тремя неизвестными . Приm=2 количество уравнений будет совпадать с количеством неизвестных. Поэтому положим m=2. В результате получается линейная система третьего порядка

, . (8.2.18)

Подставив в нее выражения для заданных узлов квадратуры, , получим систему

, . (8.2.19)

Решив эту систему в общем виде методом Гаусса, после преобразований получим

, . (8.2.20)

Таким образом, методом неопределенных коэффициентов мы получили известную нам формулу Симпсона

,

которая действительно является точной для любого многочлена третьей степени.

8.3. Метод Монте-Карло

Метод Монте-Карло называют также методом статистических испытаний. Он применяется для вычислении интегралов и для решения уравнений и задач оптимизации. Это особый подход к решению задач, основанный на теории вероятностей и математической статистике. Применение метода статистических испытаний основано на том, что компьютеры оснащены датчиками псевдослучайных чисел. Эти датчики при каждом обращении выдают значения, которые можно приближенно считать значениями случайной величины, равномерно распределенной на заданном отрезке . Таким образом, в компьютерных программах появляется возможность проводить статистические испытания и использовать статистические величины.

Рассмотрим использование метода статистических испытаний для вычисления приближенных значений интегралов.

Первая схема метода Монте-Карло

Пусть  плотность распределения вероятности случайной величины . Случайная величина. Тогда математическое ожидание величиныбудет равно

,

а дисперсия

.

Если величина равномерно распределена на отрезке, то есть

то математическое ожидание

, (8.3.1)

а дисперсия

. (8.3.2)

Статистическими оценками (приближенными значениями) математического ожидания и дисперсии являются выборочное среднее

(8.3.3)

и выборочная дисперсия

. (8.3.4)

Здесь  значения случайной величины , равномерно распределенной на отрезке, получаемые с помощью датчика случайных чисел.

Согласно центральной предельной теоремы ,по вероятности при. Кроме того,также представляет собой случайную величину, распределение вероятности которой стремится к нормальному (распределению Гаусса) прис дисперсией:

. (8.3.5)

Согласно правилу трех сигм, с вероятностью 0,997 будет выполняться неравенство

. (8.3.6)

Подставляя сюда выражения (8.3.1), (8.3.3) ,(8.3.5) и умножая обе части неравенства на получаем

. (8.3.7)

Последнее неравенство выполняется при достаточно больших значениях n с вероятностью 0,997. Таким образом, если в качестве приближенного значения интеграла выбирается величина , то оценка погрешности этого приближенного значения с вероятностью 0,997 и при достаточно большом значенииn будет равна

.

Первая алгоритмическая схема метода Монте-Карло позволяет получить приближенное значение интеграла , погрешность которого с вероятностью 0,997 не превышает заданного положительного числа. Последовательно вычисляются значенияпридо тех пор, пока не будет выполнено условие. Последнее вычисленное значениедает нам искомое приближенное значение интеграла.